北京市怀柔区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-11-10 类型：期末考试

进入出卷网下载

一、单选题

1. 16的算术平方根是 $($ $)$

A、4 B、-4 C、±4 D、8

查看试题解析
2. 盛大庄严的阅兵仪式、热烈欢腾的群众游行、雍容绽放的焰火表演、璀璨夺目的光艺展示……新中国成立70周年庆典活动令人记忆犹新.这背后彰显了中国在科技领域的飞速进步.下列庆典图片中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若分式 $\frac{x + 1}{x - 1}$ 的值等于0，则x的值为（）.

A、-1 B、1 C、0 D、2

查看试题解析
4. 下列各式中，是最简二次根式的是（）.

A、 $\sqrt{\frac{1}{3}}$ B、 $\sqrt{2}$ C、 $\sqrt{27}$ D、 $\sqrt{a^{2}}$

查看试题解析
5. 新中国成立70周年庆典阅兵直播,不仅可以通过电视观看,也可以通过手机、电脑等互联网设备进行观看.这其中,百度APP直播期间累计观看人数就达到550000000，将550000000用科学记数法表示为（）.

A、 $55 \times 10^{7}$ B、 $5.5 \times 10^{8}$ C、 $0.55 \times 10^{8}$ D、 $5.5 \times 10^{9}$

查看试题解析
6. 如图，在△ABC中，∠ABC=50°，∠BAC=20°，D为线段AB的垂直平分线与直线BC的交点，连接AD ，则∠ADC的度数为（）.

A、50° B、60° C、70° D、80°

查看试题解析
7. 如图，△ABC是等边三角形，AD是BC边上的高，E是AC的中点，P是AD上的一个动点，当PC与PE的和最小时，∠CPE的度数是（）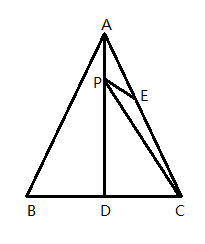

A、30° B、45° C、60° D、90°

查看试题解析
8. 下列事件中，满足随机事件且该事件每个结果发生的可能性都相等的是（）.

A、一个密封的纸箱里有7个颜色不同的球，从里面随意摸出一个球，摸出每个球的可能性相同． B、在80个相同的零件中，检验员从中取出一个零件进行检验，取出每件产品的可能性相同． C、一枚质地均匀的骰子，任意掷一次，1-6点数朝上的可能性相同． D、小东经过任意一个有红绿灯的路口，遇到红、黄和绿指示灯的可能性相同．

查看试题解析

二、填空题

9. 若式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
10. 已知 $\sqrt{a + 9}$ 是最简二次根式，且它与 $\sqrt{32}$ 是同类二次根式，则a = ．

查看试题解析
11. 如图，点 $A ， B ， D$ 在同一条直线上， $∠ A = ∠ C B E = ∠ D = 90^{o}$ ，请你只添加一个条件，使得 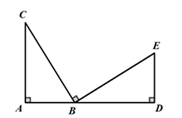$Δ A B C ≅ Δ D E B$ ．

(1)、你添加的条件是．（要求：不再添加辅助线，只需填一个答案即可）

(2)、依据所添条件，判定 $Δ A B C 与 Δ D E B$ 全等的理由是．

查看试题解析
12. 如图，在△ABC中，AB=AC ， D是AB延长线上一点，E是BC延长线上一点，F是CA延长线上一点，∠DBC=130°，则∠FAB的度数为．

查看试题解析
13. 如图在解分式方程 $\frac{2}{x^{2} - 4} + \frac{x}{x - 2} = 1$ 的过程中，步骤(2)的依据是，步骤(4)的依据是．

查看试题解析
14. 已知分式 $\frac{1 - 3 x}{2 x^{2} + 1}$ 的值为负数，则 $x$ 的取值范围为.

查看试题解析
15. 《九章算术》是中国传统数学重要的著作之一，奠定了中国传统数学的基本框架.其中第九卷《勾股》主要讲述了以测量问题为中心的直角三角形三边互求，之中记载了一道有趣的“折竹抵地”问题：
“今有竹高一丈，末折抵地，去本四尺，问折者高几何？”

译文：“一根竹子，原高一丈，一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部4尺远，则折断后的竹子高度为多少尺？”（备注：1丈=10尺）

如果设竹梢到折断处的长度为 $x$ 尺，那么折断处到竹子的根部用含 $x$ 的代数式可表示为尺，根据题意，可列方程为．

查看试题解析
16. 在每个小正方形的边长为 $1$ 的网格图形中，每个小正方形的顶点称为格点．从一个格点移动到与之相距 $\sqrt{5}$ 的另一个格点的运动称为一次跳马变换．例如，在 $4 \times 4$ 的正方形网格图形中（如图1），从点A经过一次跳马变换可以到达点B ， C ， D ， E等处．现有 $10 \times 10$ 的正方形网格图形（如图2），则从该正方形的顶点M经过跳马变换到达与其相对的N ，最少需要跳马变换的次数是，现有 $20 \times 20$ 的正方形网格图形（如图3），则从该正方形的顶点 $M^{'}$ 经过跳马变换到达与其相对的 $N^{'}$ ，最少需要跳马变换的次数是．

查看试题解析

三、解答题

17. 计算： $\sqrt[3]{- 27} + \frac{3}{\sqrt{3}} - \sqrt{12} - 3 \sqrt{\frac{1}{3}}$ ．

查看试题解析
18. 计算： $(7 + 4 \sqrt{3}) (7 - 4 \sqrt{3}) - {(3 \sqrt{5} - 1)}^{2}$

查看试题解析
19. 解方程： $\frac{x}{x + 2} = \frac{2}{x - 1} + 1$ ．

查看试题解析
20. 计算： $\frac{1}{a - b} - \frac{2 a}{a^{2} - b^{2}}$ ．

查看试题解析
21. 已知：如图，E ， F ，为AC上两点，AD∥BC ， ∠1=∠2，AE=CF ，求证：△ADF≌△CBE ．

查看试题解析
22. 化简求值： $\frac{x - 1}{x^{2} + 2 x + 1} \div (1 - \frac{2}{x + 1})$ ，其中 $x = \sqrt{3} - 1$ ．

查看试题解析
23. 已知：如图，△ABC是等边三角形，D是BC延长线上一点，且CD=CB ，连接AD ，过点D作 $D M ⊥ D B$ ，在DM上截取一点E，使得DE=AD ，连接AE ．

(1)、求证： $Δ A D B ≅ Δ A E C$ ；

(2)、猜想EC和AD的位置关系，并证明．

查看试题解析
24. 列方程解应用题：
港珠澳大桥是中国中央政府支持香港、澳门和珠三角地区城市快速发展的一项重大举措，港珠澳大桥东起香港国际机场附近的香港口岸人工岛，向西横跨伶仃洋海域后连接珠海和澳门，止于珠海洪湾，总长 55 千米，是粤港澳三地首次合作共建的超大型跨海交通工程．某天，甲乙两辆巴士均从香港口岸人工岛出发沿港珠澳大桥开往珠海洪湾，甲巴士平均每小时比乙巴士多行驶 10 千米，其行驶时间是乙巴士行驶时间的 $\frac{5}{6}$ ．求乘坐甲巴士从香港口岸人工岛出发到珠海洪湾需要多长时间．

查看试题解析
25. 数学课上，王老师布置如下任务：
如图1，直线MN外一点A ，过点A作直线MN的平行线．

(1)、小路的作法如下：
① 在MN上任取一点B ，作射线BA；

② 以B为圆心任意长为半径画弧，分别交BA和MN于C、D两点（点D位于BA的左侧），再以A为圆心，相同的长度为半径画弧EH ，交BA于点E（点E位于点A上方）；

③以E为圆心CD的长为半径画弧，交弧EH于点F（F点位于BA左侧）

④作直线AF

⑤直线AF即为所求作平行线．

请你根据小路同学的作图方法，利用直尺和圆规完成作图（保留作图痕迹）；并完成以下推理，注明其中蕴含的数学依据：

$\begin{array}{l} ∵ ∠ C B D = \underline{\begin{matrix} \begin{matrix} \end{matrix} \end{matrix}} \\ ∴ A F / / M N (\underline{\begin{matrix} \begin{matrix} \begin{matrix} \end{matrix} \end{matrix} \end{matrix}}) \end{array}$

(2)、请你参考小路的作法，利用图2再设计一种“过点A作MN的平行线”的尺规作图过程（保留作图痕迹），并说明其中蕴含的数学依据．

查看试题解析
26. 老师在黑板上书写了一个代数式的符合题意计算结果，随后用手遮住了原代数式的一部分，如下图：

(1)、求被手遮住部分的代数式，并将其化简；

(2)、原代数式的值能等于-1吗？请说明理由．

查看试题解析
27. 在探究三角形内角和等于180°的证明过程时，小明同学通过认真思考后认为，可以通过剪拼的方法将一个角剪下来，然后把这个角进行平移，从而实现把三角形的三个内角转移到一个平角中去，如图所示：

(1)、小明同学根据剪拼的过程，抽象出几何图形；并进行了推理证明，请你帮助小明完成
证明过程．

证明：过点B作BN//AC ，延长AB到M

∵ $B N / / A C$

∴ $∠ N B M = ∠ A$ （）

$∠ C B N = ∠ C$ （）

∵ $∠ C B A + ∠ C B N + ∠ N B M = 180^{o} (平角定义)$

∴ $∠ C B A + ∠ A + ∠ C = 180^{o} (等量代换)$

(2)、小军仿照小明的方法将三角形的三个内角都进行了移动，也将三个内角转移到一个平角中去，只不过平角的顶点放到了AB边上，如图所示：请你仿照小明的证明过程，抽象出几何图形再进行证明．

(3)、小兰的方法和小明以及小军的方法都不相同，她将三角形三个内角分别沿某一条直线翻折，一共进行了三次尝试，如图所示：

小兰第三次成功的关键是什么，请你写出证明思路．

查看试题解析
28. 已知： $Δ A B C ， ∠ A = 45^{\circ} ， ∠ A C B = 90^{\circ} ，$ 点D是AC延长线上一点，且 $A D = \sqrt{2} + 2 ，$ ，M是线段CD上一个动点，连接BM ，延长MB到H ，使得 $H B = M B ，$ 以点B为中心，将线段BH逆时针旋转 $45^{\circ} ，$ 得到线段BQ ，连接AQ ．

(1)、依题意补全图形；

(2)、求证： $∠ A B Q = ∠ A M B ；$

(3)、点N是射线AC上一点，且点N是点M关于点D的对称点，连接BN ，如果 $Q A = B N ，$ 求线段AB的长．

查看试题解析