北京市海淀区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-11-10 类型：期末考试

进入出卷网下载

一、单选题

1. 斐波那契螺旋线也称为“黄金螺旋线”，是根据斐波那契数列画出来的螺旋曲线，自然界中存在许多斐波那契螺旋线图案.下列斐波那契螺旋线图案中属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 2019年被称为“5G元年”．据媒体报道，5G网络的理论下载速度为1.25GB/s，这就意味着我们下载一张2.5M的照片只需要0.002s，将0.002用科学记数法表示为（）

A、 $2 \times 10^{- 2}$ B、 $2 \times 10^{- 3}$ C、 $0.2 \times 10^{- 2}$ D、 $0.2 \times 10^{- 3}$

查看试题解析
3. 下列运算结果为 $a^{6}$ 的是（）

A、 $a^{3} \cdot a^{2}$ B、 $a^{9} - a^{3}$ C、 ${(a^{2})}^{3}$ D、 $a^{18} \div a^{3}$

查看试题解析
4. 在下列因式分解的过程中，分解因式正确的是（）

A、 $x^{2} + 2 x + 4 = {(x + 2)}^{2}$ B、 $x^{2} - 4 = (x + 4) (x - 4)$ C、 $x^{2} - 4 x + 4 = {(x - 2)}^{2}$ D、 $x^{2} + 4 = {(x + 2)}^{2}$

查看试题解析
5. 如图，经过直线AB外一点C作这条直线的垂线，作法如下：
（1）任意取一点K ，使点K和点C在AB的两旁．（2）以点C为圆心，CK长为半径作弧，交AB于点D和E ．（3）分别以点D和点E为圆心，大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧相交于点F ．（4）作直线CF ．则直线CF就是所求作的垂线．根据以上尺规作图过程，若将这些点作为三角形的顶点，其中不一定是等腰三角形的为（）

A、△CDF B、△CDK C、△CDE D、△DEF

查看试题解析
6. 有两块总面积相等的场地，左边场地为正方形，由四部分构成，各部分的面积数据如图所示．右边场地为长方形，长为 $2 (a + b)$ ，则宽为（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{1}{2} (a + b)$ D、a+b

查看试题解析
7. 如图，在△ABC中，AB=AC ， D是BC边上的动点（点D与B ， C不重合），△ABD和△ACD的面积分别表示为S₁和S₂ ，下列条件不能说明AD是△ABC角平分线的是（）

A、BD=CD B、∠ADB=∠ADC C、S₁=S₂ D、AD= $\frac{1}{2}$ BC

查看试题解析
8. 如图，左边为参加2019年国庆70周年阅兵的武警摩托车礼宾护卫队，如果将每位队员看成一个点，队形可近似看成由右边所示的若干个正方形拼成的图形，其中与△ABC全等的三角形是（）

A、△AEG B、△ADF C、△DFG D、△CEG

查看试题解析
9. 若 $a b = - 4$ ，其中 $a > b$ ，以下分式中一定比 $\frac{b}{a}$ 大的是（）

A、 $\frac{2 b}{2 a}$ B、 $\frac{2 b}{a}$ C、 $- \frac{2}{a}$ D、 $\frac{b + 2}{a}$

查看试题解析
10. 已知长方形ABCD可以按图示方式分成九部分，在a ， b变化的过程中，下面说法正确的有（）
①图中存在三部分的周长之和恰好等于长方形ABCD的周长②长方形ABCD的长宽之比可能为2③当长方形ABCD为正方形时，九部分都为正方形④当长方形ABCD的周长为60时，它的面积可能为100

A、①② B、①③ C、②③④ D、①③④

查看试题解析

二、填空题

11. 请写出一个只含有字母x的分式，当x=3时分式的值为0，你写的分式是．

查看试题解析
12. 计算： ${(2 a)}^{3} \cdot {(- a)}^{4} \div a^{2} =$ ．

查看试题解析
13. 如图，要测量池塘两岸相对的两点A ， B的距离，可以在池塘外取AB的垂线BF上的两点C ， D ，使BC=CD ，再画出BF的垂线DE ，使E与A ， C在一条直线上.若想知道两点A ， B的距离，只需要测量出线段即可．

查看试题解析
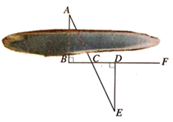14. 如图，已知空间站A与星球B距离为a ，信号飞船C在星球B附近沿圆形轨道行驶，B ， C之间的距离为b ．数据S表示飞船C与空间站A的实时距离，那么S的最大值是．

查看试题解析
15. 平面直角坐标系xOy中，点A（4，3），点B（3，0），点C（5，3），点E在x轴上.当CE=AB时，点E的坐标为．

查看试题解析

16. 北京大兴国际机场于2019年9月25日正式投入运营.小贝和小京分别从草桥和北京站出发赶往机场乘坐飞机，出行方式及所经过的站点与路程如下表所示：

出行方式	途径站点	路程
地铁	草桥—大兴新城—大兴机场	全程约43公里
公交	北京站—蒲黄榆—榴乡桥—大兴机场	全程约54公里

由于地面交通拥堵，地铁的平均速度约为公交平均速度的两倍，于是小贝比小京少用了半小时到达机场.若设公交的平均速度为x公里/时，根据题意可列方程: ．

查看试题解析

17. 如图，△ABC中，AD平分∠BAC ， CD⊥AD ，若∠ABC与∠ACD互补，CD=5，则BC的长为．

查看试题解析
18. 如图，已知 $∠ M O N$ ，在边 $O N$ 上顺次取点 $P_{1}$ ， $P_{3}$ ， $P_{5}$ …，在边 $O M$ 上顺次取点 $P_{2}$ ， $P_{4}$ ， $P_{6}$ …，使得 $O P_{1} = P_{1} P_{2} = P_{2} P_{3} = P_{3} P_{4} = P_{4} P_{5}$ …，得到等腰△ $O P_{1} P_{2}$ ，△ $P_{1} P_{2} P_{3}$ ，△ $P_{2} P_{3} P_{4}$ ，△ $P_{3} P_{4} P_{5}$ …

(1)、若 $∠ M O N$ =30°，可以得到的最后一个等腰三角形是；

(2)、若按照上述方式操作，得到的最后一个等腰三角形是△ $P_{3} P_{4} P_{5}$ ，则 $∠ M O N$ 的度数 $α$ 的取值范围是．

查看试题解析

三、解答题

19.

(1)、计算： ${(3 - π)}^{0} - 3^{8} \div 3^{6} + {(\frac{1}{3})}^{- 1}$

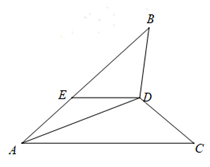
(2)、因式分解： $3 x^{2} - 12 y^{2}$

查看试题解析
20. 如图，已知AB=AC，E为AB上一点，ED∥AC，ED=AE.求证：BD=CD.

查看试题解析
21. 已知 $a^{2} - 2 a b + b^{2} = 0$ ，求代数式 $a (4 a - b) - (2 a + b) (2 a - b)$ 的值．

查看试题解析
22. 如图，AB⊥AC，AB=AC，过点B，C分别向射线AD作垂线，垂足分别为E，F.

(1)、依题意补全图形；

(2)、求证：BE=EF+FC.

查看试题解析
23. 已知 $x = a + b - 2$ ， $y - 2 a b = a^{2} + b^{2}$ ．

(1)、用x表示y；

(2)、求代数式 $(x - \frac{4}{x}) \cdot \frac{x}{y} + \frac{4}{x + 2}$ 的值．

查看试题解析
24. 如图所示，将两个含30°角的三角尺摆放在一起，可以证得△ABD是等边三角形，于是我们得到：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.

交换命题的条件和结论，得到下面的命题：

在直角△ABC中，∠ACB=90°，如果 $C B = \frac{1}{2} A B$ ，那么∠BAC=30°．

请判断此命题的真假，若为真命题，请给出证明；若为假命题，请说明理由.

查看试题解析

25. 对于代数式，不同的表达形式能表现出它的不同性质．例如代数式

A = x^{2} - 4 x + 5

，若将其写成

A = {(x - 2)}^{2} + 1

的形式，就能看出不论字母x取何值，它都表示正数；若将它写成

A = {(x - 1)}^{2} - 2 (x - 1) + 2

的形式，就能与代数式B=

x^{2} - 2 x + 2

建立联系．下面我们改变x的值，研究一下A ， B两个代数式取值的规律：

x	-2	-1	0	1	2	3
$B = x^{2} - 2 x + 2$	10	5	2	1		5
$A = {(x - 1)}^{2} - 2 (x - 1) + 2$	17	10	5

(1)、完成上表；

(2)、观察表格可以发现：

若x=m时， $B = x^{2} - 2 x + 2 = n$ ，则x=m+1时， $A = x^{2} - 4 x + 5 = n$ ．我们把这种现象称为代数式A参照代数式B取值延后，此时延后值为1．

①若代数式D参照代数式B取值延后，相应的延后值为2，求代数式D；

②已知代数式 $a x^{2} - 10 x + b$ 参照代数式 $3 x^{2} - 4 x + c$ 取值延后，请直接写出b-c的值：．

查看试题解析

26. 如图，在△ABC中，AB=AC，∠BAC=90°，点D是边BC上的动点，连接AD，点C关于直线AD的对称点为点E，射线BE与射线AD交于点F.

(1)、在图1中，依题意补全图形；

(2)、记 $∠ D A C = α$ （ $α < 45 °$ ），求 $∠ A B F$ 的大小；（用含 $α$ 的式子表示）

(3)、若△ACE是等边三角形，猜想EF和BC的数量关系，并证明.

查看试题解析
27. 在平面直角坐标系xOy中，直线 $l$ 为一、三象限角平分线．点P关于y轴的对称点称为P的一次反射点，记作 $P_{1}$ ； $P_{1}$ 关于直线 $l$ 的对称点称为点P的二次反射点，记作 $P_{2}$ ．例如，点 $(- 2 ， 5)$ 的一次反射点为 $(2 ， 5)$ ，二次反射点为 $(5 ， 2)$ ．根据定义，回答下列问题：

(1)、点 $(2 ， 5)$ 的一次反射点为，二次反射点为；

(2)、当点A在第一象限时，点 $M (3 ， 1)$ ， $N (3 ， - 1)$ ， $Q (- 1 ， - 3)$ 中可以是点A的二次反射点的是；

(3)、若点A在第二象限，点 $A_{1}$ ， $A_{2}$ 分别是点A的一次、二次反射点，△ $O A_{1} A_{2}$ 为等边三角形，求射线OA与x轴所夹锐角的度数．

查看试题解析
28. 在平面直角坐标系xOy中，直线 $l$ 为一、三象限角平分线．点P关于y轴的对称点称为P的一次反射点，记作 $P_{1}$ ； $P_{1}$ 关于直线 $l$ 的对称点称为点P的二次反射点，记作 $P_{2}$ ．若点A在 $y$ 轴左侧，点 $A_{1}$ ， $A_{2}$ 分别是点A的一次、二次反射点，△ $A A_{1} A_{2}$ 是等腰直角三角形，请直接写出点A在平面直角坐标系xOy中的位置．

查看试题解析