2017年吉林省长春市中考数学试卷
试卷更新日期：2017-09-30 类型：中考真卷
一、选择题
-
1. 3的相反数是（ ）A、﹣3 B、﹣ C、 D、32. 据统计，2016年长春市接待旅游人数约67000000人次，67000000这个数用科学记数法表示为（ ）A、67×106 B、6.7×105 C、6.7×107 D、6.7×1083. 下列图形中，可以是正方体表面展开图的是（ ）A、
B、
C、
D、
4. 不等式组 的解集为（ ）A、x＜﹣2 B、x≤﹣1 C、x≤1 D、x＜35. 如图，在△ABC中，点D在AB上，点E在AC上，DE∥BC．若∠A=62°，∠AED=54°，则∠B的大小为（ ）
A、54° B、62° C、64° D、74°6. 如图，将边长为3a的正方形沿虚线剪成两块正方形和两块长方形．若拿掉边长2b的小正方形后，再将剩下的三块拼成一块矩形，则这块矩形较长的边长为（ ）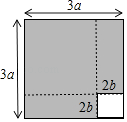
A、3a+2b B、3a+4b C、6a+2b D、6a+4b7. 如图，点A，B，C在⊙O上，∠ABC=29°，过点C作⊙O的切线交OA的延长线于点D，则∠D的大小为（ ）
A、29° B、32° C、42° D、58°8. 如图，在平面直角坐标系中，平行四边形OABC的顶点A的坐标为（﹣4，0），顶点B在第二象限，∠BAO=60°，BC交y轴于点D，DB：DC=3：1．若函数y= （k＞0，x＞0）的图象经过点C，则k的值为（ ）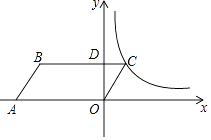
A、 B、 C、 D、二、填空题
-
9. 若关于x的一元二次方程x2+4x+a=0有两个相等的实数根，则a的值是 ．10. 如图，直线a∥b∥c，直线l1 ， l2与这三条平行线分别交于点A，B，C和点D，E，F．若AB：BC=1：2，DE=3，则EF的长为 ．
11. 如图，则△ABC中，∠BAC=100°，AB=AC=4，以点B为圆心，BA长为半径作圆弧，交BC于点D，则 的长为 ． （结果保留π）
12. 如图1，这个图案是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”．此图案的示意图如图2，其中四边形ABCD和四边形EFGH都是正方形，△ABF、△BCG、△CDH、△DAE是四个全等的直角三角形．若EF=2，DE=8，则AB的长为 ．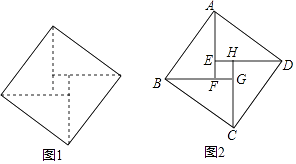
13. 如图，在平面直角坐标系中，△ABC的顶点A在第一象限，点B，C的坐标为（2，1），（6，1），∠BAC=90°，AB=AC，直线AB交x轴于点P．若△ABC与△A'B'C'关于点P成中心对称，则点A'的坐标为 ．
三、解答题
-
14. 先化简，再求值：3a（a2+2a+1）﹣2（a+1）2 ， 其中a=2．
15. 一个不透明的口袋中有一个小球，上面分别标有字母a，b，c，每个小球除字母不同外其余均相同，小园同学从口袋中随机摸出一个小球，记下字母后放回且搅匀，再从可口袋中随机摸出一个小球记下字母．用画树状图（或列表）的方法，求小园同学两次摸出的小球上的字母相同的概率．
16. 如图，某商店营业大厅自动扶梯AB的倾斜角为31°，AB的长为12米，求大厅两层之间的距离BC的长．（结果精确到0.1米）（参考数据：sin31°=0.515，cos31°=0.857，tan31°=0.60）
17. 某校为了丰富学生的课外体育活动，购买了排球和跳绳．已知排球的单价是跳绳的单价的3倍，购买跳绳共花费750元，购买排球共花费900元，购买跳绳的数量比购买排球的数量多30个，求跳绳的单价．
18. 如图，在菱形ABCD中，∠A=110°，点E是菱形ABCD内一点，连结CE绕点C顺时针旋转110°，得到线段CF，连结BE，DF，若∠E=86°，求∠F的度数．
19. 某校八年级学生会为了解本年级600名学生的睡眠情况，将同学们某天的睡眠时长t（小时）分为A，B，C，D，E（A：9≤t≤24；B：8≤t＜9；C：7≤t＜8；D：6≤t＜7；E：0≤t＜6）五个选项，进行了一次问卷调查，随机抽取n名同学的调查问卷并进行了整理，绘制成如下条形统计图，根据统计图提供的信息解答下列问题：
(1)、求n的值；(2)、根据统计结果，估计该年级600名学生中睡眠时长不足7小时的人数．
20. 甲、乙两车间同时开始加工一批服装．从开始加工到加工完这批服装甲车间工作了9小时，乙车间在中途停工一段时间维修设备，然后按停工前的工作效率继续加工，直到与甲车间同时完成这批服装的加工任务为止．设甲、乙两车间各自加工服装的数量为y（件）．甲车间加工的时间为x（时），y与x之间的函数图象如图所示．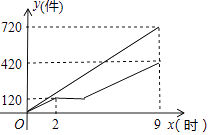
(1)、甲车间每小时加工服装件数为件；这批服装的总件数为件．
(2)、求乙车间维修设备后，乙车间加工服装数量y与x之间的函数关系式；(3)、求甲、乙两车间共同加工完1000件服装时甲车间所用的时间．21. 【再现】如图①，在△ABC中，点D，E分别是AB，AC的中点，可以得到：DE∥BC，且DE= BC．（不需要证明）
(1)、【探究】如图②，在四边形ABCD中，点E，F，G，H分别是AB，BC，CD，DA的中点，判断四边形EFGH的形状，并加以证明．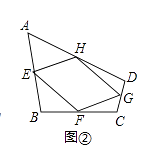
(2)、【应用】在（1）【探究】的条件下，四边形ABCD中，满足什么条件时，四边形EFGH是菱形？你添加的条件是： ． （只添加一个条件）(3)、如图③，在四边形ABCD中，点E，F，G，H分别是AB，BC，CD，DA的中点，对角线AC，BD相交于点O．若AO=OC，四边形ABCD面积为5，则阴影部分图形的面积和为 ．
22. 如图①，在Rt△ABC中，∠C=90°，AB=10，BC=6，点P从点A出发，沿折线AB﹣BC向终点C运动，在AB上以每秒5个单位长度的速度运动，在BC上以每秒3个单位长度的速度运动，点Q从点C出发，沿CA方向以每秒 个单位长度的速度运动，P，Q两点同时出发，当点P停止时，点Q也随之停止．设点P运动的时间为t秒．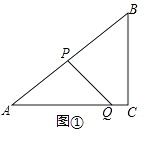
(1)、求线段AQ的长；（用含t的代数式表示）(2)、连结PQ，当PQ与△ABC的一边平行时，求t的值；(3)、如图②，过点P作PE⊥AC于点E，以PE，EQ为邻边作矩形PEQF，点D为AC的中点，连结DF．设矩形PEQF与△ABC重叠部分图形的面积为S．①当点Q在线段CD上运动时，求S与t之间的函数关系式；②直接写出DF将矩形PEQF分成两部分的面积比为1：2时t的值．
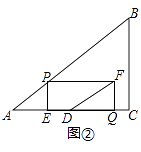23. 定义：对于给定的两个函数，任取自变量x的一个值，当x＜0时，它们对应的函数值互为相反数；当x≥0时，它们对应的函数值相等，我们称这样的两个函数互为相关函数．例如：一次函数y=x﹣1，它的相关函数为y= ．(1)、已知点A（﹣5，8）在一次函数y=ax﹣3的相关函数的图象上，求a的值；(2)、已知二次函数y=﹣x2+4x﹣ ．①当点B（m， ）在这个函数的相关函数的图象上时，求m的值；②当﹣3≤x≤3时，求函数y=﹣x2+4x﹣ 的相关函数的最大值和最小值；
(3)、在平面直角坐标系中，点M，N的坐标分别为（﹣ ，1），（ ，1），连结MN．直接写出线段MN与二次函数y=﹣x2+4x+n的相关函数的图象有两个公共点时n的取值范围．