2017年湖北省武汉市中考数学试卷

试卷更新日期：2017-09-30 类型：中考真卷

进入出卷网下载

一、选择题

1. 计算 $\sqrt{36}$ 的结果为（）

A、6 B、﹣6 C、18 D、﹣18

查看试题解析
2. 若代数式 $\frac{1}{a - 4}$ 在实数范围内有意义，则实数a的取值范围为（）

A、a=4 B、a＞4 C、a＜4 D、a≠4

查看试题解析
3. 下列计算的结果是x⁵的为（）

A、x¹⁰÷x² B、x⁶﹣x C、x²•x³ D、（x²）³

查看试题解析
4. 在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示：
成绩/m
1.50
1.60
1.65
1.70
1.75
1.80
人数
2
3
2
3
4
1
则这些运动员成绩的中位数、众数分别为（）

A、1.65、1.70 B、1.65、1.75 C、1.70、1.75 D、1.70、1.70

查看试题解析
5. 计算（x+1）（x+2）的结果为（）

A、x²+2 B、x²+3x+2 C、x²+3x+3 D、x²+2x+2

查看试题解析
6. 点A（﹣3，2）关于y轴对称的点的坐标为（）

A、（3，﹣2） B、（3，2） C、（﹣3，﹣2） D、（2，﹣3）

查看试题解析
7. 某物体的主视图如图所示，则该物体可能为（）

A、 B、 C、 D、

查看试题解析
8. 按照一定规律排列的n个数：﹣2、4、﹣8、16、﹣32、64、…，若最后三个数的和为768，则n为（）

A、9 B、10 C、11 D、12

查看试题解析
9. 已知一个三角形的三边长分别为5、7、8，则其内切圆的半径为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{3}{2}$ C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析
10. 如图，在Rt△ABC中，∠C=90°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为（）

A、4 B、5 C、6 D、7

查看试题解析

二、填空题

11. 计算2×3+（﹣4）的结果为．

查看试题解析
12. 计算 $\frac{x}{x + 1}$ ﹣ $\frac{1}{x + 1}$ 的结果为．

查看试题解析
13. 如图，在▱ABCD中，∠D=100°，∠DAB的平分线AE交DC于点E，连接BE．若AE=AB，则∠EBC的度数为．

查看试题解析
14. 一个不透明的袋中共有5个小球，分别为2个红球和3个黄球，它们除颜色外完全相同．随机摸出两个小球，摸出两个颜色相同的小球的概率为．

查看试题解析
15. 如图，在△ABC中，AB=AC=2 $\sqrt{3}$ ，∠BAC=120°，点D，E都在边BC上，∠DAE=60°．若BD=2CE，则DE的长为．

查看试题解析
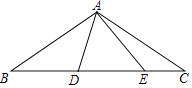16. 已知关于x的二次函数y=ax²+（a²﹣1）x﹣a的图象与x轴的一个交点的坐标为（m，0）．若2＜m＜3，则a的取值范围是．

查看试题解析

三、解答题

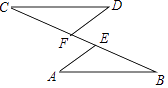
17. 解方程：4x﹣3=2（x﹣1）

查看试题解析
18. 如图，点C，F，E，B在一条直线上，∠CFD=∠BEA，CE=BF，DF=AE，写出CD与AB之间的关系，并证明你的结论．

查看试题解析
19. 某公司共有A，B，C三个部门，根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
各部门人数及每人所创年利润统计表
部门
员工人数
每人所创的年利润/万元
A
5
10
B
b
8
C
c
5

(1)、①在扇形图中，C部门所对应的圆心角的度数为
②在统计表中，b= ， c=

(2)、求这个公司平均每人所创年利润．

查看试题解析
20. 某公司为奖励在趣味运动会上取得好成绩的员工，计划购买甲、乙两种奖品共20件．其中甲种奖品每件40元，乙种奖品每件30元

(1)、如果购买甲、乙两种奖品共花费了650元，求甲、乙两种奖品各购买了多少件？

(2)、如果购买乙种奖品的件数不超过甲种奖品件数的2倍，总花费不超过680元，求该公司有哪几种不同的购买方案？

查看试题解析
21. 如图，△ABC内接于⊙O，AB=AC，CO的延长线交AB于点D

(1)、求证：AO平分∠BAC；

(2)、若BC=6，sin∠BAC= $\frac{3}{5}$ ，求AC和CD的长．

查看试题解析
22. 如图，直线y=2x+4与反比例函数y= $\frac{k}{x}$ 的图象相交于A（﹣3，a）和B两点

(1)、求k的值；

(2)、直线y=m（m＞0）与直线AB相交于点M，与反比例函数的图象相交于点N．若MN=4，求m的值；

(3)、直接写出不等式 $\frac{6}{x - 5}$ ＞x的解集．

查看试题解析
23. 已知四边形ABCD的一组对边AD、BC的延长线交于点E．

(1)、如图1，若∠ABC=∠ADC=90°，求证：ED•EA=EC•EB；

(2)、如图2，若∠ABC=120°，cos∠ADC= $\frac{3}{5}$ ，CD=5，AB=12，△CDE的面积为6，求四边形ABCD的面积；

(3)、如图3，另一组对边AB、DC的延长线相交于点F．若cos∠ABC=cos∠ADC= $\frac{3}{5}$ ，CD=5，CF=ED=n，直接写出AD的长（用含n的式子表示）

查看试题解析
24. 已知点A（﹣1，1）、B（4，6）在抛物线y=ax²+bx上

(1)、求抛物线的解析式；

(2)、如图1，点F的坐标为（0，m）（m＞2），直线AF交抛物线于另一点G，过点G作x轴的垂线，垂足为H．设抛物线与x轴的正半轴交于点E，连接FH、AE，求证：FH∥AE；

(3)、如图2，直线AB分别交x轴、y轴于C、D两点．点P从点C出发，沿射线CD方向匀速运动，速度为每秒 $\sqrt{2}$
个单位长度；同时点Q从原点O出发，沿x轴正方向匀速运动，速度为每秒1个单位长度．点M是直线PQ与抛物线的一个交点，当运动到t秒时，QM=2PM，直接写出t的值．

查看试题解析

成绩/m	1.50	1.60	1.65	1.70	1.75	1.80
人数	2	3	2	3	4	1

部门	员工人数	每人所创的年利润/万元
A	5	10
B	b	8
C	c	5