2017年广西贺州市中考数学试卷
试卷更新日期:2017-09-30 类型:中考真卷
一、选择题
-
1. 的倒数是( )A、﹣2 B、2 C、 D、2. 下列各图中,∠1与∠2互为邻补角的是( )A、
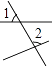 B、
B、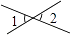 C、
C、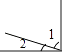 D、
D、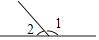 3. 下列式子中是分式的是( )A、 B、 C、 D、4. 一条关于数学学习方法的微博在一周内转发了318000次,将318000用科学记数法可以表示为( )
3. 下列式子中是分式的是( )A、 B、 C、 D、4. 一条关于数学学习方法的微博在一周内转发了318000次,将318000用科学记数法可以表示为( )
A、3.18×105 B、31.8×105 C、318×104 D、3.18×1045. 现有相同个数的甲、乙两组数据,经计算得: = ,且S甲2=0.35,S乙2=0.25,比较这两组数据的稳定性,下列说法正确的是( )
A、甲比较稳定 B、乙比较稳定 C、甲、乙一样稳定 D、无法确定6. 下列图形中,既是中心对称图形又是轴对称图形的是( )
A、正五边形 B、平行四边形 C、矩形 D、等边三角形7. 如图,在△ABC中,点D,E分别为AB,AC的中点,则△ADE与四边形BCED的面积比为( )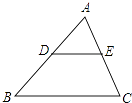 A、1:1 B、1:2 C、1:3 D、1:48. 小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是( )
A、1:1 B、1:2 C、1:3 D、1:48. 小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是( )
A、 B、
B、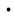 C、
C、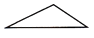 D、
D、 9. 不等式组 的解集在数轴上表示正确的是( )A、
9. 不等式组 的解集在数轴上表示正确的是( )A、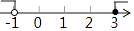 B、
B、 C、
C、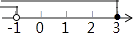 D、
D、 10. 一次函数y=ax+a(a为常数,a≠0)与反比例函数y= (a为常数,a≠0)在同一平面直角坐标系内的图象大致为( )
10. 一次函数y=ax+a(a为常数,a≠0)与反比例函数y= (a为常数,a≠0)在同一平面直角坐标系内的图象大致为( )
A、 B、
B、 C、
C、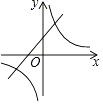 D、
D、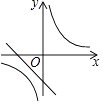 11. 如图,在⊙O中,AB是⊙O的直径,AB=10, = = ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
11. 如图,在⊙O中,AB是⊙O的直径,AB=10, = = ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( ) A、1 B、2 C、3 D、412. 将一组数 ,2, ,2 , ,…,2 ,按下列方式进行排列:
A、1 B、2 C、3 D、412. 将一组数 ,2, ,2 , ,…,2 ,按下列方式进行排列:,2, ,2 , ;
2 , ,4,3 ,2 ;
…
若2的位置记为(1,2),2 的位置记为(2,1),则 这个数的位置记为( )
A、(5,4) B、(4,4) C、(4,5) D、(3,5)二、填空题
-
13. 要使代数式 有意义,则x的取值范围是 .14. 为了调查某市中小学生对“营养午餐”的满意程度,适合采用的调查方式是 . (填“全面调查”或“抽样调查”)
15. 将多项式2mx2﹣8mx+8m分解因式的结果是 .16. 如图,在Rt△ABC中,∠A=60°,AB=1,将Rt△ABC绕点C按顺时针方向旋转到△A1B1C的位置,点A1刚好落在BC的延长线上,求点A从开始到结束所经过的路径长为(结果保留π) .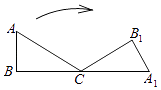 17. 二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,下列结论:①abc<0;②2a+b<0;③b2﹣4ac=0;④8a+c<0;⑤a:b:c=﹣1:2:3,其中正确的结论有 .
17. 二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,下列结论:①abc<0;②2a+b<0;③b2﹣4ac=0;④8a+c<0;⑤a:b:c=﹣1:2:3,其中正确的结论有 .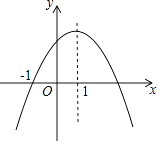 18. 如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE=2,DF=3,则AH的长为 .
18. 如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE=2,DF=3,则AH的长为 .
三、解答题
-
19. 计算:(﹣1)2017+ ﹣(π﹣3)0+2cos30°.20. 先化简,再求值: ÷(1+ ),其中x= +1.21. 在“植树节”期间,小王、小李两人想通过摸球的方式来决定谁去参加学校植树活动,规则如下:在两个盒子内分别装入标有数字1,2,3,4的四个和标有数字1,2,3的三个完全相同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于6,那么小王去,否则就是小李去.
(1)、用树状图或列表法求出小王去的概率;(2)、小李说:“这种规则不公平”,你认同他的说法吗?请说明理由.22. 如图,某武警部队在一次地震抢险救灾行动中,探险队员在相距4米的水平地面A,B两处均探测出建筑物下方C处有生命迹象,已知在A处测得探测线与地面的夹角为30°,在B处测得探测线与地面的夹角为60°,求该生命迹象C处与地面的距离.(结果精确到0.1米,参考数据: ≈1.41, ≈1.73)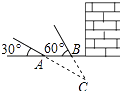 23. 政府为了美化人民公园,计划对公园某区域进行改造,这项工程先由甲工程队施工10天完成了工程的 ,为了加快工程进度,乙工程队也加入施工,甲、乙两个工程队合作10天完成了剩余的工程,求乙工程队单独完成这项工程需要几天.
23. 政府为了美化人民公园,计划对公园某区域进行改造,这项工程先由甲工程队施工10天完成了工程的 ,为了加快工程进度,乙工程队也加入施工,甲、乙两个工程队合作10天完成了剩余的工程,求乙工程队单独完成这项工程需要几天.
24. 如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O.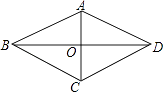 (1)、求证:四边形ABCD是菱形;(2)、若CD=3,BD=2 ,求四边形ABCD的面积.25. 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
(1)、求证:四边形ABCD是菱形;(2)、若CD=3,BD=2 ,求四边形ABCD的面积.25. 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD. (1)、求证:AF⊥EF;(2)、若AC=6,CF=2,求⊙O的半径.26. 如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=﹣x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(﹣4,0),抛物线的顶点为点D.
(1)、求证:AF⊥EF;(2)、若AC=6,CF=2,求⊙O的半径.26. 如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=﹣x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(﹣4,0),抛物线的顶点为点D.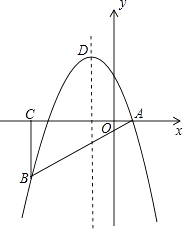 (1)、求抛物线的解析式;(2)、点E是直角三角形ABC斜边AB上的一个动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段FE的长度最大时,求点E的坐标;(3)、在(2)的条件下,抛物线上是否存在一点P,使△PEF是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点E是直角三角形ABC斜边AB上的一个动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段FE的长度最大时,求点E的坐标;(3)、在(2)的条件下,抛物线上是否存在一点P,使△PEF是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.