2017年广西桂林市中考数学试卷
试卷更新日期:2017-09-30 类型:中考真卷
一、选择题
-
1. 2017的绝对值是( )A、2017 B、﹣2017 C、0 D、2. 4的算术平方根是( )
A、4 B、2 C、﹣2 D、±23. 一组数据2,3,5,7,8的平均数是( )A、2 B、3 C、4 D、54. 如图所示的几何体的主视图是( )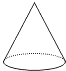 A、
A、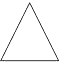 B、
B、 C、
C、 D、
D、 5. 下列图形中不是中心对称图形的是( )A、
5. 下列图形中不是中心对称图形的是( )A、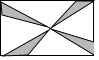 B、
B、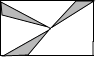 C、
C、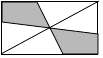 D、
D、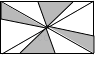 6. 用科学记数法表示数57000000为( )A、57×106 B、5.7×106 C、5.7×107 D、0.57×1087. 下列计算正确的是( )A、a3÷a3=a B、(x2)3=x5 C、m2•m4=m6 D、2a+4a=8a8. 如图,直线a,b被直线c所截,下列条件能判断a∥b的是( )
6. 用科学记数法表示数57000000为( )A、57×106 B、5.7×106 C、5.7×107 D、0.57×1087. 下列计算正确的是( )A、a3÷a3=a B、(x2)3=x5 C、m2•m4=m6 D、2a+4a=8a8. 如图,直线a,b被直线c所截,下列条件能判断a∥b的是( )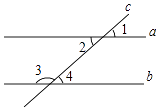 A、∠1=∠2 B、∠1=∠4 C、∠3+∠4=180° D、∠2=30°,∠4=35°9. 下列命题是真命题的是( )A、相等的角是对顶角 B、若实数a,b满足a2=b2 , 则a=b C、若实数a,b满足a<0,b<0,则ab<0 D、角的平分线上的点到角的两边的距离相等10. 若分式 的值为0,则x的值为( )A、﹣2 B、0 C、2 D、±211. 一次函数y=﹣x+1(0≤x≤10)与反比例函数y= (﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
A、∠1=∠2 B、∠1=∠4 C、∠3+∠4=180° D、∠2=30°,∠4=35°9. 下列命题是真命题的是( )A、相等的角是对顶角 B、若实数a,b满足a2=b2 , 则a=b C、若实数a,b满足a<0,b<0,则ab<0 D、角的平分线上的点到角的两边的距离相等10. 若分式 的值为0,则x的值为( )A、﹣2 B、0 C、2 D、±211. 一次函数y=﹣x+1(0≤x≤10)与反比例函数y= (﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )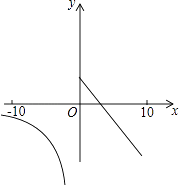 A、﹣ ≤x≤1 B、﹣ ≤x≤ C、﹣ ≤x≤ D、1≤x≤12. 如图,在菱形ABCD中,∠ABC=60°,AB=4,点E是AB边上的动点,过点B作直线CE的垂线,垂足为F,当点E从点A运动到点B时,点F的运动路径长为( )
A、﹣ ≤x≤1 B、﹣ ≤x≤ C、﹣ ≤x≤ D、1≤x≤12. 如图,在菱形ABCD中,∠ABC=60°,AB=4,点E是AB边上的动点,过点B作直线CE的垂线,垂足为F,当点E从点A运动到点B时,点F的运动路径长为( )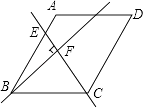 A、 B、2 C、 π D、 π
A、 B、2 C、 π D、 π二、填空题
-
13. 分解因式:x2﹣x= .14. 如图,点D是线段AB的中点,点C是线段AD的中点,若CD=1,则AB= .
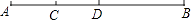 15. 分式 与 的最简公分母是 .16. 一个不透明的口袋中有6个完全相同的小球,把它们分别标号为1,2,3,4,5,6,从中随机摸取一个小球,取出的小球标号恰好是偶数的概率是 .17. 如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则 的值为 .
15. 分式 与 的最简公分母是 .16. 一个不透明的口袋中有6个完全相同的小球,把它们分别标号为1,2,3,4,5,6,从中随机摸取一个小球,取出的小球标号恰好是偶数的概率是 .17. 如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则 的值为 .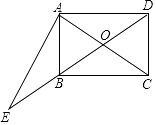 18. 如图,第一个图形中有1个点,第二个图形中有4个点,第三个图形中有13个点,…,按此规律,第n个图形中有个点.
18. 如图,第一个图形中有1个点,第二个图形中有4个点,第三个图形中有13个点,…,按此规律,第n个图形中有个点.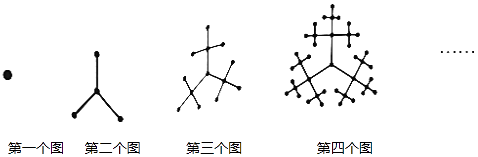
三、解答题
-
19. 计算:(﹣2017)0﹣sin30°+ +2﹣1 .20. 解二元一次方程组: .21. 某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:
组别
阅读时间t(单位:小时)
频数(人数)
A
0≤t<1
8
B
1≤t<2
20
C
2≤t<3
24
D
3≤t<4
m
E
4≤t<5
8
F
t≥5
4
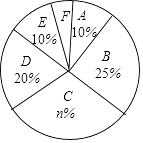 (1)、图表中的m= , n=;(2)、扇形统计图中F组所对应的圆心角为度;(3)、该校共有学生1500名,请估计该校有多少名学生的每周平均课外阅读时间不低于3小时?22. 如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的顶点叫做格点,线段AB的端点均在格点上.
(1)、图表中的m= , n=;(2)、扇形统计图中F组所对应的圆心角为度;(3)、该校共有学生1500名,请估计该校有多少名学生的每周平均课外阅读时间不低于3小时?22. 如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的顶点叫做格点,线段AB的端点均在格点上.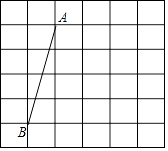 (1)、将线段AB向右平移3个单位长度,得到线段A′B′,画出平移后的线段并连接AB′和A′B,两线段相交于点O;(2)、求证:△AOB≌△B′OA′.23. “C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)
(1)、将线段AB向右平移3个单位长度,得到线段A′B′,画出平移后的线段并连接AB′和A′B,两线段相交于点O;(2)、求证:△AOB≌△B′OA′.23. “C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)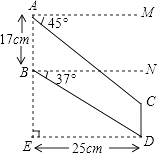 24. 为进一步促进义务教育均衡发展,某市加大了基础教育经费的投入,已知2015年该市投入基础教育经费5000万元,2017年投入基础教育经费7200万元.(1)、求该市这两年投入基础教育经费的年平均增长率;(2)、如果按(1)中基础教育经费投入的年平均增长率计算,该市计划2018年用不超过当年基础教育经费的5%购买电脑和实物投影仪共1500台,调配给农村学校,若购买一台电脑需3500元,购买一台实物投影需2000元,则最多可购买电脑多少台?
24. 为进一步促进义务教育均衡发展,某市加大了基础教育经费的投入,已知2015年该市投入基础教育经费5000万元,2017年投入基础教育经费7200万元.(1)、求该市这两年投入基础教育经费的年平均增长率;(2)、如果按(1)中基础教育经费投入的年平均增长率计算,该市计划2018年用不超过当年基础教育经费的5%购买电脑和实物投影仪共1500台,调配给农村学校,若购买一台电脑需3500元,购买一台实物投影需2000元,则最多可购买电脑多少台?
25. 已知:如图,在△ABC中,AB=BC=10,以AB为直径作⊙O分别交AC,BC于点D,E,连接DE和DB,过点E作EF⊥AB,垂足为F,交BD于点P.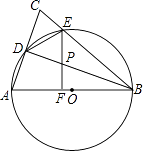 (1)、求证:AD=DE;
(1)、求证:AD=DE;
(2)、若CE=2,求线段CD的长;(3)、在(2)的条件下,求△DPE的面积.
26. 已知抛物线y1=ax2+bx﹣4(a≠0)与x轴交于点A(﹣1,0)和点B(4,0).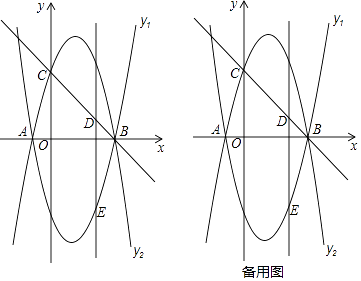 (1)、求抛物线y1的函数解析式;(2)、如图①,将抛物线y1沿x轴翻折得到抛物线y2 , 抛物线y2与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线y1于点E,求线段DE的长度的最大值;(3)、在(2)的条件下,当线段DE处于长度最大值位置时,作线段BC的垂直平分线交DE于点F,垂足为H,点P是抛物线y2上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.
(1)、求抛物线y1的函数解析式;(2)、如图①,将抛物线y1沿x轴翻折得到抛物线y2 , 抛物线y2与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线y1于点E,求线段DE的长度的最大值;(3)、在(2)的条件下,当线段DE处于长度最大值位置时,作线段BC的垂直平分线交DE于点F,垂足为H,点P是抛物线y2上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.