2016年高考理数真题试卷（全国丙卷）

试卷更新日期：2016-06-14 类型：高考真卷

进入出卷网下载

一、选择题:本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 设集合S={x|（x﹣2）（x﹣3）≥0}，T={x|x＞0}，则S∩T=（　　）

A、[2，3] B、（﹣∞，2]∪[3，+∞） C、[3，+∞） D、（0，2]∪[3，+∞）

查看试题解析
2. 若z=1+2i，则 $\frac{4 i}{z \vec{z} - 1}$ =（　　）

A、1 B、﹣1 C、i D、﹣i

查看试题解析
3. 已知向量 $\vec{B A}$ =（ $\frac{1}{2}$ ， $\frac{\sqrt{3}}{2}$ ）， $\vec{B C}$ =（ $\frac{\sqrt{3}}{2}$ ， $\frac{1}{2}$ ），则∠ABC=（　　）

A、30° B、45° C、60° D、120°

查看试题解析
4.
某旅游城市为向游客介绍本地的气温情况，绘制了一年中各月平均最高气温和平均最低气温的雷达图，图中A点表示十月的平均最高气温约为15℃，B点表示四月的平均最低气温约为5℃，下面叙述不正确的是（　　）

A、各月的平均最低气温都在0℃以上 B、七月的平均温差比一月的平均温差大 C、三月和十一月的平均最高气温基本相同 D、平均最高气温高于20℃的月份有5个

查看试题解析
5. 若tanα= $\frac{3}{4}$ ，则cos²α+2sin2α=（　　）

A、 $\frac{64}{25}$ B、 $\frac{48}{25}$ C、1 D、 $\frac{16}{25}$

查看试题解析
6. 已知a= $2^{\frac{4}{3}}$ ，b= $3^{\frac{2}{3}}$ ，c= $25^{\frac{1}{3}}$ ，则（　　）

A、b＜a＜c B、a＜b＜c C、b＜c＜a D、c＜a＜b

查看试题解析
7.
执行如图程序框图，如果输入的a=4，b=6，那么输出的n=（　　）

A、3 B、4 C、5 D、6

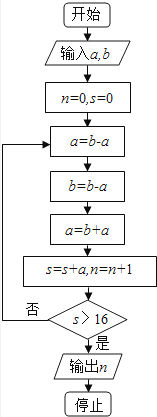查看试题解析
8. 在△ABC中，B= $\frac{π}{4}$ ，BC边上的高等于 $\frac{1}{3}$ BC，则cosA=（　　）

A、 $\frac{3 \sqrt{10}}{10}$ B、 $\frac{\sqrt{10}}{10}$ C、﹣ $\frac{\sqrt{10}}{10}$ D、﹣ $\frac{3 \sqrt{10}}{10}$

查看试题解析
9.
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为（　　）

A、18+36 $\sqrt{5}$ B、54+18 $\sqrt{5}$ C、90 D、81

查看试题解析
10. 在封闭的直三棱柱ABC﹣A₁B₁C₁内有一个体积为V的球，若AB⊥BC，AB=6，BC=8，AA₁=3，则V的最大值是（　　）

A、4π B、 $\frac{9 π}{2}$ C、6π D、 $\frac{32 π}{3}$

查看试题解析
11. 已知O为坐标原点，F是椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的左焦点，A，B分别为C的左，右顶点．P为C上一点，且PF⊥x轴，过点A的直线l与线段PF交于点M，与y轴交于点E．若直线BM经过OE的中点，则C的离心率为（　　）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
12. 定义“规范01数列”{a_n}如下：{a_n}共有2m项，其中m项为0，m项为1，且对任意k≤2m，a₁ ， a₂ ， …，a_k中0的个数不少于1的个数，若m=4，则不同的“规范01数列”共有（　　）

A、18个 B、16个 C、14个 D、12个

查看试题解析

二、填空题：本大题共4小题，每小题5分.

13. 若x，y满足约束条件 ${\begin{cases} x - y + 1 \geq 0 \\ x - 2 y \leq 0 \\ x + 2 y - 2 \leq 0 \end{cases}$ ，则z=x+y的最大值为．

查看试题解析
14. 函数y=sinx﹣ $\sqrt{3}$ cosx的图象可由函数y=sinx+ $\sqrt{3}$ cosx的图象至少向右平移个单位长度得到．

查看试题解析
15. 已知f（x）为偶函数，当x＜0时，f（x）=ln（﹣x）+3x，则曲线y=f（x）在点（1，﹣3）处的切线方程是．

查看试题解析
16. 已知直线l：mx+y+3m﹣ $\sqrt{3}$ =0与圆x²+y²=12交于A，B两点，过A，B分别作l的垂线与x轴交于C，D两点，若|AB|=2 $\sqrt{3}$ ，则|CD|= ．

查看试题解析

三、解答题：解答应写出文字说明，证明过程或演算步骤.

17. 已知数列{a_n}的前n项和S_n=1+λa_n ，其中λ≠0．

(1)、证明{a_n}是等比数列，并求其通项公式；

(2)、若S₅= $\frac{31}{32}$ ，求λ．

查看试题解析
18.
如图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图．
注：年份代码1﹣7分别对应年份2008﹣2014．

(1)、由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以证明；

(2)、建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量．
附注：
参考数据： $\sum_{i = 1}^{7} y_{i}$ =9.32， $\sum_{i = 1}^{7} t_{i} y_{i}$ =40.17， $\sqrt{\sum_{i = 1}^{7} {(y_{i} - \bar{y})}^{2}}$ =0.55， $\sqrt{7}$ ≈2.646．
参考公式： $r = \frac{\sum_{i = 1}^{7} (t_{i} - \bar{t}) (y_{i} - \bar{y})}{\sqrt{\sum_{i = 1}^{n} {(t_{i} - \bar{t})}^{2} \sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}}$ ，
回归方程 $\hat{y} = \hat{a} + \hat{b} t$ 中斜率和截距的最小二乘估计公式分别为：
$\hat{b} = \frac{\sum_{i = 1}^{n} (t_{i} - \bar{t}) (y_{i} - \bar{y})}{\sqrt{\sum_{i = 1}^{n} {(t_{i} - \bar{t})}^{2} \sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}}$ ， $\hat{a} = \hat{y} - \hat{b} \bar{t}$ ．

查看试题解析
19.
如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．

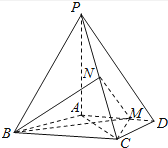(1)、证明：MN∥平面PAB；

(2)、求直线AN与平面PMN所成角的正弦值．

查看试题解析
20. 已知抛物线C：y²=2x的焦点为F，平行于x轴的两条直线l₁ ， l₂分别交C于A，B两点，交C的准线于P，Q两点．

(1)、若F在线段AB上，R是PQ的中点，证明AR∥FQ；

(2)、若△PQF的面积是△ABF的面积的两倍，求AB中点的轨迹方程．

查看试题解析
21. 设函数f（x）=acos2x+（a﹣1）（cosx+1），其中a＞0，记f（x）的最大值为A．

(1)、求f′（x）；

(2)、求A；

(3)、证明：|f′（x）|≤2A．

查看试题解析
22.
[选修4-1：几何证明选讲]如图，⊙O中弧AB 的中点为P，弦PC，PD分别交AB于E，F两点．

(1)、若∠PFB=2∠PCD，求∠PCD的大小；

(2)、若EC的垂直平分线与FD的垂直平分线交于点G，证明：OG⊥CD．

查看试题解析
23. [选修4-4：坐标系与参数方程]
在直角坐标系xOy中，曲线C₁的参数方程为 ${\begin{cases} x = \sqrt{3} \cos α \\ y = \sin α \end{cases}$ （α为参数），以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，曲线C₂的极坐标方程为ρsin（θ+ $\frac{π}{4}$ ）=2 $\sqrt{2}$ ．

(1)、写出C₁的普通方程和C₂的直角坐标方程；

(2)、设点P在C₁上，点Q在C₂上，求|PQ|的最小值及此时P的直角坐标．

查看试题解析
24. [选修4-5：不等式选讲]
已知函数f（x）=|2x﹣a|+a．

(1)、当a=2时，求不等式f（x）≤6的解集；

(2)、设函数g（x）=|2x﹣1|，当x∈R时，f（x）+g（x）≥3，求a的取值范围．

查看试题解析