安徽省宿州市十三所省重点中学2019-2020学年高一上学期数学期末联考试卷

试卷更新日期：2020-11-06 类型：期末考试

进入出卷网下载

一、单选题

1. $\sin 480 °$ 的值是（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $- \frac{\sqrt{3}}{2}$

查看试题解析
2. 已知函数 $f (x) = \cos π x$ ，则下列正确的是（）

A、 $f (x)$ 是周期为1的奇函数 B、 $f (x)$ 是周期为2的偶函数 C、 $f (x)$ 是周期为1的非奇非偶函数 D、 $f (x)$ 是周期为2的非奇非偶函数

查看试题解析
3. 已知AM是 $△ A B C$ 的BC边上的中线，若 $\vec{A B} = \vec{a}$ ， $\vec{A C} = \vec{b}$ ，则 $\vec{A M}$ 等于（）

A、 $\frac{1}{2} (\vec{a} - \vec{b})$ B、 $- \frac{1}{2} (\vec{a} - \vec{b})$ C、 $\frac{1}{2} (\vec{a} + \vec{b})$ D、 $- \frac{1}{2} (\vec{a} + \vec{b})$

查看试题解析
4. 已知 $\tan α = 3$ ，则 $\frac{\sin α + \cos α - 2}{\sin α - \cos α}$ 的值为（）

A、 $2 - \sqrt{10}$ B、 $2 - \frac{\sqrt{10}}{10}$ C、 $2 \pm \sqrt{10}$ D、 $2 \pm \frac{\sqrt{10}}{10}$

查看试题解析
5. 要得到函数 $y = s i n （ 4 x -$ $\frac{π}{3}$ $）$ 的图象，只需要将函数 $y = s i n 4 x$ 的图象（）

A、向左平移 $\frac{π}{12}$ 个单位 B、向右平移 $\frac{π}{12}$ 个单位 C、向左平移 $\frac{π}{3}$ 个单位 D、向右平移 $\frac{π}{3}$ 个单位

查看试题解析
6. 函数 $f (x) = \log_{a} (x + 2) (0 < a < 1)$ 的图象必不过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 在单位圆中，面积为1的扇形的圆心角为（）

A、1弧度 B、2弧度 C、3弧度 D、4弧度

查看试题解析
8. 已知 $\cos θ - \sin θ > 1$ ，则角 $θ$ 的终边在（）

A、第二象限 B、第三象限 C、第二象限或第四象限 D、第四象限

查看试题解析
9. 已知向量 $\vec{a} = (- 2, 0), \vec{a} - \vec{b} = (- 3, - 1)$ ，则下列结论正确的是（）

A、 $\vec{a} \cdot \vec{b} = 2$ B、 $\vec{a} / / \vec{b}$ C、 $| \vec{a} | = | \vec{b} |$ D、 $\vec{b} ⊥ (\vec{a} + \vec{b})$

查看试题解析
10. 集合 $A = {x | \sin x + \lg \cos x = 1}$ 是（）

A、 $\emptyset$ B、单元素集 C、二元素集 D、无限集

查看试题解析
11. 函数 $y = \log_{a} x$ （ $a > 0$ 且 $a \neq 1$ ）按照向量 $\vec{a} = (3,2)$ 平移后的图象过定点P，且角 $α$ 的终边过点P，则 $\sin α + 2 \cos α$ 的值为（）

A、 $\frac{7}{5}$ B、 $\frac{6}{5}$ C、 $\sqrt{5}$ D、 $\frac{3}{5} \sqrt{5}$

查看试题解析
12. $\sin α$ ， $\sin β$ 是方程 $2 {(\log_{\frac{1}{4}} x)}^{2} - \log_{\frac{1}{4}} x + \frac{1}{16} = 0$ 的两个实根，则 $\cos α \cdot \cos β$ 的取值范围是（）

A、 $[- \frac{1}{2}, \frac{1}{2}]$ B、 $(- \frac{1}{2}, \frac{1}{2})$ C、 $(0, \frac{1}{2})$ D、 $(- \frac{1}{2}, 0)$

查看试题解析

二、填空题

13. 已知幂函数y=f（x）的图象过点（2， $\sqrt{2}$ ），则f（9）= ．

查看试题解析
14. 如图所示为函数 $y = A \sin (ω x + φ) + 2$ ， $(| φ | < π)$ 的图像的一部分，它的解析式为.

查看试题解析
15. 实数x，y满足 $\log_{\frac{1}{2}} \sin x + | {(\frac{1}{3})}^{y} - 3 | = 0$ ，则 $2^{\cos x} + 4^{y}$ 的值为.

查看试题解析
16. 下面六个句子中，错误的题号是.
①周期函数必有最小正周期；

②若 $\vec{a} \cdot \vec{b} = 0$ 则 $\vec{a}$ ， $\vec{b}$ 至少有一个为 $\vec{0}$ ；

③ $α$ 为第三象限角，则 $\cos (\sin a) < 0$ ；

④若向量 $\vec{a}$ 与 $\vec{b}$ 的夹角为锐角，则 $\vec{a} \cdot \vec{b} > 0$ ；

⑤存在 $α$ ， $β \in R$ ，使 $\sin (a + β) = \sin a + \sin β$ 成立；

⑥在 $△ A B C$ 中，O为 $△ A B C$ 内一点，且 $\vec{O A} + \vec{O B} + \vec{O C} = \vec{0}$ ，则O为 $△ A B C$ 的重心.

查看试题解析

三、解答题

17. 化简： $\frac{\cos (θ + π) \cdot \sin^{2} (θ + 3 π)}{\tan (θ + 4 π) \cdot \tan (θ - π) \cdot \cos^{2} (- π - θ)}$ .

查看试题解析
18. 已知 $\vec{a} = (1, 2)$ ， $\vec{b} = (- 2, 1)$ ，k为何值时，

(1)、 $k \vec{a} + \vec{b}$ 与 $\vec{a} - \vec{b}$ 垂直？

(2)、 $k \vec{a} + \vec{b}$ 与 $\vec{a} - \vec{b}$ 平行？

查看试题解析
19. 已知向量 $\vec{a} = (2 \sin x ， \cos x)$ ， $\vec{b} = (\sqrt{3} \cos x ， 2 \cos x)$ ，定义函数 $f (x) = \vec{a} \cdot \vec{b} - 1$ .

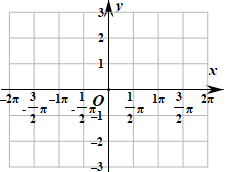(1)、求函数 $f (x)$ 的单调递减区间；

(2)、画出函数 $y = f (x)$ ， $x \in [- \frac{7 π}{12} ， \frac{5 π}{12}]$ 的图像.

查看试题解析
20. 已知 $y = f (x)$ 的定义域为R且满足条件.
①当 $x > 0$ 时， $f (x) < 0$ ；

②对任意实数x，y，都有 $f (x + y) = f (x) + f (y)$ .

(1)、求 $f (0)$ ，并证明 $f (x)$ 为奇函数；

(2)、判断并证明 $f (x)$ 的单调性.

查看试题解析
21. 已知锐角 $△ A B C$ 中， $\sin (A + B) = \frac{3}{5}$ ， $\sin (A - B) = \frac{1}{5}$ .

(1)、求证： $\tan A = 2 \tan B$ ；

(2)、设 $A B = 3$ ，求 $A B$ 边上的高.

查看试题解析
22. 如图，在同一个平面内，向量 $\vec{O A}$ ， $\vec{O B}$ ， $\vec{O C}$ 的模分别为1，1， $\sqrt{2}$ ， $\vec{O A}$ 与 $\vec{O C}$ 的夹角为 $α$ ，且 $\tan α = 7$ ， $\vec{O B}$ 与 $\vec{O C}$ 的夹角为 $45 °$ .若 $\vec{O C} = m \vec{O A} + n \vec{O B} (m ， n \in R)$ ，

(1)、求 $\log_{\frac{5}{7}} n - \log_{\frac{5}{7}} m$ 的值；

(2)、若函数 $f (x) = a x^{2} - 2 a x + \frac{1}{8} (a < 0)$ 在 $[m ， n]$ 上的最大值为2，求a的值.

查看试题解析