广西壮族自治区贵港市桂平市2019-2020学年高二上学期理数期末考试试卷

试卷更新日期：2020-11-06 类型：期末考试

进入出卷网下载

一、单选题

1. 抛物线 $x^{2} = 4 y$ 的焦点坐标是（）

A、 $(1 ， 0)$ B、 $(0 ， 1)$ C、 $(2 ， 0)$ D、 $(0 ， 2)$

查看试题解析
2. 已知向量 $\overset{⇀}{a} = (2, 3, 4)$ ， $\overset{⇀}{b} = (1, - m, 2)$ ，若 $\overset{⇀}{a} / / \overset{⇀}{b}$ ，则 $m =$ （）

A、 $\frac{3}{2}$ B、 $- \frac{3}{2}$ C、 $\frac{10}{3}$ D、 $- \frac{10}{3}$

查看试题解析
3. 某班有60名学生，其中男生有40人，现将男、女学生用分层抽样法抽取12人观看校演讲总决赛，则该班中被抽取观看校演讲总决赛的女生人数为（）

A、8 B、6 C、4 D、2

查看试题解析
4. 若椭圆 $\frac{x^{2}}{49} + \frac{y^{2}}{32} = 1$ 上的一点 $M$ 到其左焦点的距离是6，则点 $M$ 到其右焦点的距离是（）

A、5 B、6 C、7 D、8

查看试题解析
5. 甲、乙两人近五次某项测试成绩的得分情况如图所示，则（）

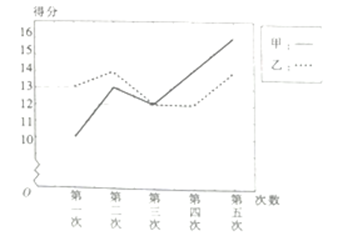A、甲得分的平均数比乙的大 B、乙的成绩更稳定 C、甲得分的中位数比乙的大 D、甲的成绩更稳定

查看试题解析
6. 给出下列四个说法，其中正确的是（）

A、命题“若 $\sqrt{x + 1} > 1$ ，则 $x > 0$ ”的否命题是“若 $\sqrt{x + 1} > 1$ ，则 $x \leq 0$ ” B、“ $m > 3$ ”是“双曲线 $\frac{x^{2}}{9} - \frac{y^{2}}{m^{2}} = 1$ 的离心率大于 $\sqrt{2}$ ”的充要条件 C、命题“ $\exists x_{0} > 0$ ， $x_{0}^{2} + 3 x_{0} + 1 < 0$ ”的否定是“ $\exists x_{0} > 0$ ， $x_{0}^{2} + 3 x_{0} + 1 \geq 0$ ” D、命题“在 $Δ A B C$ 中，若 $A + B > \frac{π}{2}$ ，则 $Δ A B C$ 是锐角三角形”的逆否命题是假命题

查看试题解析
7. 从装有完全相同的4个红球和2个黄球的盒子中任取2个小球，则互为对立事件的是（）

A、“至少一个红球”与“至少一个黄球” B、“至多一个红球”与“都是红球” C、“都是红球”与“都是黄球” D、“至少一个红球”与“至多一个黄球”

查看试题解析
8. 已知直线 $l$ ： $x - y + 3 = 0$ 与双曲线 $C$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 交于 $A$ ， $B$ 两点，点 $P (1, 4)$ 是弦 $A B$ 的中点，则双曲线 $C$ 的渐近线方程是（）

A、 $y = \pm 4 x$ B、 $y = \pm \frac{1}{4} x$ C、 $y = \pm \frac{1}{2} x$ D、 $y = \pm 2 x$

查看试题解析
9. 求 $1 + \frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \frac{1}{9} + \dots + \frac{1}{2019}$ 的程序框图，如图所示，则图中判断框中可填入（）

A、 $n \leq 1010 ?$ B、 $n \leq 1011 ?$ C、 $n \leq 1012 ?$ D、 $n \leq 2019 ?$

查看试题解析
10. 已知点 $P$ 在椭圆 $C$ ： $\frac{x^{2}}{4} + y^{2} = 1$ 上，直线 $l$ ： $x - y + m = 0$ ，则“ $m = 3 \sqrt{5}$ ”是“点 $P$ 到直线 $l$ 的距离的最小值是 $\sqrt{10}$ ”的（）

A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
11. 已知椭圆 $C$ ： $\frac{x^{2}}{9} + \frac{y^{2}}{5} = 1$ 的左、右焦点分别是 $F_{1}$ ， $F_{2}$ ，点 $P$ 在椭圆 $C$ 上，且 $∠ P F_{1} F_{2} = 60 °$ ，则 $Δ P F_{1} F_{2}$ 的面积是（）

A、5 B、 $\frac{5}{2}$ C、 $5 \sqrt{3}$ D、 $\frac{5 \sqrt{3}}{2}$

查看试题解析
12. 已知双曲线 $C$ ： $\frac{x^{2}}{4} - \frac{y^{2}}{5} = 1$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ，点 $P$ 在双曲线 $C$ 上.若 $Δ P F_{1} F_{2}$ 为钝角三角形，则 $| P F_{1} | + | P F_{2} |$ 的取值范围是（）

A、 $(9 ， + \infty)$ B、 $(0 ， 2 \sqrt{14}) \cup (9 ， + \infty)$ C、 $(6 ， 2 \sqrt{14}) \cup (9 ， + \infty)$ D、 $(6 ， 2 \sqrt{14})$

查看试题解析

二、填空题

13. 若抛物线 $y^{2} = 2 p x (p > 0)$ 经过点 $(2, 1)$ ，则 $p =$ .

查看试题解析
14. 如图，在四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，底面 $A B C D$ 是平行四边形，点 $E$ 为 $B D$ 的中点，若 $\overset{⇀}{A_{1} E} = x \overset{⇀}{A A_{1}} + y \overset{⇀}{A B} + z \overset{⇀}{A D}$ ，则 $x + y + z =$ .

查看试题解析
15. 若投掷一枚质地均匀的骰子，第一次投掷的点数为 $a$ ，第二次投掷的点数为 $b$ ，则 $b > a$ 的概率为.

查看试题解析
16. 已知抛物线 $C$ ： $y^{2} = 4 x$ ，点 $Q$ 在 $x$ 轴上，直线 $l$ ： $(m - 2) x - y - 2 m + 4 = 0$ 与抛物线 $C$ 交于 $M$ ， $N$ 两点，若直线 $Q M$ 与直线 $Q N$ 的斜率互为相反数，则点 $Q$ 的坐标是.

查看试题解析

三、解答题

17. 众所周知，城市公交车的数量太多会造成资源的浪费，太少又难以满足乘客的需求，为此，某市公交公司在某站台的50名候车乘客中随机抽取10名，统计了他们的候车时间（单位：分钟），得到下表.

候车时间

人数

$[0, 5)$

1

$[5, 10)$

4

$[10, 15)$

2

$[15, 20)$

2

$[20, 25]$

1

(1)、估计这10名乘客的平均候车时间（同一组中的每个数据可用该组区间的中点值代替）；

(2)、估计这50名乘客的候车时间少于10分钟的人数.

查看试题解析
18. 已知抛物线 $C$ ： $y^{2} = 2 p x (p > 0)$ 的焦点为 $F$ ，准线方程是 $x = - 2$ .

(1)、求抛物线 $C$ 的方程；

(2)、过点 $F$ 且倾斜角为 $\frac{π}{4}$ 的直线 $l$ 与抛物线 $C$ 交于 $A$ ， $B$ 两点，求 $| A B |$ ；

(3)、设点 $M$ 在抛物线 $C$ 上，且 $| M F | = 6$ ，求 $Δ O F M$ 的面积（ $O$ 为坐标原点）.

查看试题解析

19. 某幼儿园举办“yue”主题系列活动——“悦”动越健康亲子运动打卡活动，为了解小朋友坚持打卡的情况，对该幼儿园所有小朋友进行了调查，调查结果如下表：

打卡天数	17	18	19	20	21
男生人数	3	5	3	7	2
女生人数	3	5	5	7	3

(1)、根据上表数据，求该幼儿园男生平均打卡的天数；

(2)、若从打卡21天的小朋友中任选2人交流心得，求选到男生和女生各1人的概率.

查看试题解析

20. 某公司为了解某产品的获利情况，将今年1至7月份的销售收入

x

（单位：万元）与纯利润

y

（单位：万元）的数据进行整理后，得到如下表格：

月份	1	2	3	4	5	6	7
销售收入 $x$	13	13.5	13.8	14	14.2	14.5	15
纯利润 $y$	3.2	3.8	4	4.2	4.5	5	5.5

该公司先从这7组数据中选取5组数据求纯利润 $y$ 关于销售收入 $x$ 的线性回归方程，再用剩下的2组数据进行检验.假设选取的是2月至6月的数据.

参考公式： $s_{x y} = \frac{x_{1} y_{1} + x_{2} y_{2} + \dots + x_{n} y_{n}}{n} - \bar{x} \bar{y}$ ， $s_{x}^{2} = \frac{{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + \dots + {(x_{n} - \bar{x})}^{2}}{n}$ ， $b = \frac{s_{x y}}{s_{x}^{2}}$ ， $a = \bar{y} - b \bar{x}$ ；参考数据： $x_{2} y_{2} + x_{3} y_{3} + \dots + x_{6} y_{6} = 301.7$ .

(1)、求纯利润

y

关于销售收入

x

的线性回归方程（精确到0.01）；

(2)、若由线性回归方程得到的估计数据与检验数据的误差均不超过0.1万元，则认为得到的线性回归方程是理想的.试问该公司所得线性回归方程是否理想？

查看试题解析

21. 如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，底面 $A B C$ 是边长为4的等边三角形， $∠ A_{1} A B = ∠ A_{1} A C$ ， $D$ 为 $B C$ 的中点.

(1)、证明： $B C ⊥$ 平面 $A_{1} A D$ .

(2)、若 $Δ A_{1} A D$ 是等边三角形，求二面角 $D - A A_{1} - C$ 的正弦值.

查看试题解析
22. 已知椭圆 $E$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的焦距为 $2 \sqrt{2}$ ，点 $A$ 在椭圆 $E$ 上，且 $| O A |$ 的最小值是 $\sqrt{2}$ （ $O$ 为坐标原点）.

(1)、求椭圆 $E$ 的标准方程.

(2)、已知动直线 $l$ 与圆 $O$ ： $x^{2} + y^{2} = t^{2} (t > 0)$ 相切，且与椭圆 $E$ 交于 $P$ ， $Q$ 两点.是否存在实数 $t$ ，使得 $O P ⊥ O Q$ ？若存在，求出 $t$ 的值；若不存在，请说明理由.

查看试题解析

候车时间	人数
$[0, 5)$	1
$[5, 10)$	4
$[10, 15)$	2
$[15, 20)$	2
$[20, 25]$	1