江苏省扬州市江都区八校2021届九年级上学期数学10月联考试卷

试卷更新日期：2020-11-06 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列方程中，是关于x的一元二次方程的是（）

A、ax²+bx+c=0 B、x²﹣y﹣1=0 C、 $\frac{1}{x}$ +x=1 D、x²=0

查看试题解析
2. 若关于x的一元二次方程－2m－3＝0有一个根为0，则m的值是（）

A、3 B、－1 C、3或－1 D、－3或1

查看试题解析
3. 若n（n≠0）是关于x的方程x²+mx+n=0的根，则m+n的值为（）

A、-2 B、-1 C、1 D、2

查看试题解析
4. 已知⊙O的直径为10，点P到点O的距离大于8，那么点P的位置（）

A、一定在⊙O的内部 B、一定在⊙O的外部 C、一定在⊙O的上 D、不能确定

查看试题解析
5. 某超市一月份的营业额为100万元，已知第一季度的总营业额共1000万元，如果平均每月增长率为x，则由题意列方程应为（）

A、100（1+x）²=1000 B、100+100×2x=1000 C、100+100×3x=1000 D、100[1+（1+x）+（1+x）²]=1000

查看试题解析
6. 如图，⊙O的半径为5，弦AB=8，M是弦AB上的动点，则OM不可能为（）

A、2 B、3 C、4 D、5

查看试题解析
7. 已知方程x²- $2 \sqrt{2}$ x+2m=0有两个实数根，则 $\sqrt{{(m - 1)}^{2}}$ 的化简结果是（）

A、m-1 B、m+1 C、1-m D、±（m-1）

查看试题解析
8. 已知关于 $x$ 的方程 $x^{2} - 6 x + (a - 2) | x - 3 | + 9 - 2 a = 0$ 有且仅有两个不相等的实根，则实数 $a$ 的取值范围为（）

A、 $a = - 2$ B、 $a > 0$ C、 $a = - 2$ 或a>0 D、 $a \leq - 2$ 或a>0

查看试题解析

二、填空题

9. 一元二次方程x²＝2x的解为.

查看试题解析
10. 已知一元二次方程（m﹣2）x²﹣4x+m²﹣4=0的一个根为0，则m=.

查看试题解析
11. 如果方程kx²+3x+1=0有两个不等实数根，则实数k的取值范围是

查看试题解析
12. 若m是方程2x²﹣5x﹣1=0的一个根，则6m²﹣15m+2015的值为.

查看试题解析
13. 设m，n分别为一元二次方程 $x^{2} - 2 x - 2015 = 0$ 的两个实数根，则 $m^{2} - 3 m - n$ =.

查看试题解析
14.
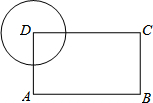
如图，在矩形ABCD中，AB=4，AD=3，以顶点D为圆心作半径为r的圆，若要求另外三个顶点A、B、C中至少有一个点在圆内，且至少有一个点在圆外，则r的取值范围是．

查看试题解析
15. 如果关于x的方程x²＋2（a＋1）x＋2a＋1＝0有一个小于2的正数根，那么实数a的取值范围是.

查看试题解析
16. 如图，在⊙O中，AB＝2CD，那么 $\overset{⌢}{A B}$ 2 $\overset{⌢}{C D}$ （填“＞，＜或＝”）

查看试题解析
17. 如图，在以AB为直径的半圆中， $\overset{⌢}{A D}$ = $\overset{⌢}{E B}$ ，CD⊥AB，EF⊥AB，CD=CF=1，则以AC和BC的长为两根的一元二次方程是.

查看试题解析
18. 如果m，n是两个不相等的实数，且满足m²﹣m=3，n²﹣n=3，那么代数式2n²﹣mn+2m+2015=.

查看试题解析

三、解答题

19. 解下列方程：

(1)、2x²＋3x=1

(2)、 ${(x - 3)}^{2} + 3 x (3 - x)$ ＝0

查看试题解析
20. 如图，已知AB是⊙O的直径，M，N分别为AO，BO的中点，CM⊥AB，DN⊥AB，垂足分别为M，N.求证：AC=BD.

查看试题解析
21. 已知：平行四边形ABCD的两边AB，AD的长是关于x的方程 $x^{2} - m x + \frac{m}{2} - \frac{1}{4}$ ＝0的两个实数根.

(1)、当m为何值时，平行四边形ABCD是菱形？求出这时菱形的边长；

(2)、若AB的长为1，那么平行四边形ABCD的周长是多少？

查看试题解析
22. 如图，在⊙O中，半径OC⊥弦AB，垂足为点D，AB＝6，CD＝1.求⊙O半径的长.

查看试题解析
23. 已知关于x的方程x²－（k＋2）x＋2k＝0.

(1)、求证：k取任何实数值，方程总有实数根；

(2)、若等腰三角形一边长为4，另两边长b，c恰好是这个方程的两个根，求△ABC的周长.

查看试题解析
24. 如图，为美化环境，某小区计划在一块长为60m，宽为40m的长方形空地上修建一个长方形花圃，并将花圃四周余下的空地修建同样宽的通道，当通道的面积与花圃的面积之比等于3：5时，求此时通道的宽．

查看试题解析
25. 某品牌童装平均每天可售出 $40$ 件，每件盈利 $40$ 元.为了迎接“元旦”，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽量减少库存.经市场调查发现：如果每件童装降价0.5元，那么平均每天就可多售出2件.

(1)、要想平均每天销售这种童装上盈利 $2400$ 元，那么每件童装应降价多少元？

(2)、用配方法说明：要想盈利最多，每件童装应降价多少元？

查看试题解析
26. 如图，已知△ABC是边长为3cm的等边三角形，动点P、Q同时从A、B两点出发(点P不与点A、B重合，点Q不与点B、C重合)，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间为ts，则当t为何值时，△PBQ是直角三角形？

查看试题解析
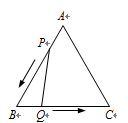27. 选取二次三项式 $a x^{2} + b x + c (a \neq 0)$ 中的两项，配成完全平方式的过程叫配方.
例如：①选取二次项和一次项配方： $x^{2} - 4 x + 2 = （ x - 2 ）^{2} - 2$ ；

②选取二次项和常数项配方： $x^{2} - 4 x + 2 = {(x- \sqrt{2})}^{2} + (2 \sqrt{2} - 4) x$ ，或 $x^{2} - 4 x + 2 = {(x + \sqrt{2})}^{2} + (4 + 2 \sqrt{2}) x$

③选取一次项和常数项配方： $x^{2} - 4 x + 2 = （ \sqrt{2} x - \sqrt{2} ）^{2} - x^{2}$

根据上述材料，解决下面问题：

(1)、写出 $x^{2} - 4 x + 4$ 的两种不同形式的配方；

(2)、已知 $x^{2} + y^{2} + xy- 3 y + 3 = 0$ ，求 $x^{y}$ 的值.

(3)、若关于 $x$ 的代数式 $9 x^{2} - （ m + 6 ） x + m - 2$ 是完全平方式，求 $m$ 的值.

查看试题解析
28. 如果方程x²+px+q=0有两个实数根x₁ ， x₂ ，那么x₁+x₂=﹣p，x₁x₂=q，请根据以上结论，解决下列问题：

(1)、已知a、b是方程x²+15x+5=0的二根，则 $\frac{a}{b} + \frac{b}{a}$ =?

(2)、已知a、b、c满足a+b+c=0，abc=16，求正数c的最小值.

(3)、结合二元一次方程组的相关知识，解决问题：已知 ${\begin{matrix} x = x_{1} \\ y = y_{1} \end{matrix}$ 和 ${\begin{matrix} x = x_{2} \\ y = y_{2} \end{matrix}$ 是关于x，y的方程组 ${\begin{matrix} x^{2} - y + k = 0 \\ x - y = 1 \end{matrix}$ 的两个不相等的实数解.问：是否存在实数k，使得y₁y₂﹣ $\frac{x_{1}}{x_{2}} - \frac{x_{2}}{x_{1}}$ =2？若存在，求出的k值，若不存在，请说明理由.

查看试题解析