江苏省连云港市灌云县西片2021届九年级上学期数学第一次月考试卷
试卷更新日期:2020-11-06 类型:月考试卷
一、单选题
-
1. 下列方程中,属于一元二次方程的是( )A、x+1=0 B、x2=2x﹣1 C、2y﹣x=1 D、x2+3=2. 已知方程x2﹣(k+1)x+3k=0的一个根是2,则k为( )A、﹣2 B、﹣3 C、3 D、13. 用配方法解方程 时,原方程变形为( )A、 B、 C、 D、4. 受益于电子商务的发展以及法治环境的改善等多重因素,“快递业”成为我国经济的一匹“黑马”2018年我国快递业务量为500亿件,2020年快递量预计将达到740亿件,若设快递量平均每年增长率为x,则下列方程中,正确的是( )A、500(1+x)2=740 B、500(1+2x)=740 C、500(1+x)=740 D、500(1﹣x)2=7405. 已知 的直径是10, 点到圆心 的距离为4,则 点与 的位置关系是( )A、在圆外 B、在圆内 C、在圆上 D、无法确定6. 如图, 外接圆的圆心坐标是( )
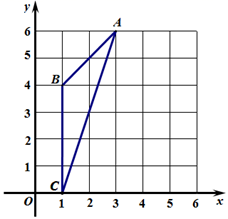 A、(5,2) B、(2,3) C、(1,4) D、(0,0)7. 如图,AB是⊙O的直径,C和D是⊙O上两点,连接AC,BC,BD,CD,若∠CDB=36°,则∠ABC=( )
A、(5,2) B、(2,3) C、(1,4) D、(0,0)7. 如图,AB是⊙O的直径,C和D是⊙O上两点,连接AC,BC,BD,CD,若∠CDB=36°,则∠ABC=( )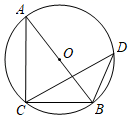 A、36° B、44° C、54° D、72°8. 如图,在半径为3的⊙O中, 是直径, 是弦,D是 的中点, 与 交于点E.若E是 的中点,则 的长是( )
A、36° B、44° C、54° D、72°8. 如图,在半径为3的⊙O中, 是直径, 是弦,D是 的中点, 与 交于点E.若E是 的中点,则 的长是( )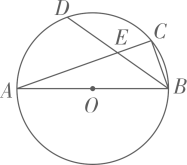 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 把方程3x(x﹣2)=4(x+1)化为一元二次方程的一般形式是;
10. 如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是. 11. 如图,⊙O是△ABC的外接圆,∠A=30°,BC=4,则⊙O的直径为.
11. 如图,⊙O是△ABC的外接圆,∠A=30°,BC=4,则⊙O的直径为.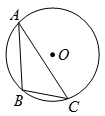 12. 在一次新年聚会中,小朋友们互相赠送礼物,全部小朋友共互赠了110件礼物,若假设参加聚会小朋友的人数为x人,则根据题意可列方程为.13. 如图,四边形 ABCD 内接于⊙O,已知∠ADC=140°,则∠AOC=°.
12. 在一次新年聚会中,小朋友们互相赠送礼物,全部小朋友共互赠了110件礼物,若假设参加聚会小朋友的人数为x人,则根据题意可列方程为.13. 如图,四边形 ABCD 内接于⊙O,已知∠ADC=140°,则∠AOC=°. 14. 关于x的一元二次方程kx2﹣4x+3=0有实数根,则k应满足的条件是.15. 石拱桥是中国传统桥梁四大基本形式之一,如图,已知一石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,求水面宽AB=m.
14. 关于x的一元二次方程kx2﹣4x+3=0有实数根,则k应满足的条件是.15. 石拱桥是中国传统桥梁四大基本形式之一,如图,已知一石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,求水面宽AB=m. 16. 关于x的方程x2﹣(3k+1)x+2k2+2k=0,若等腰三角形△ABC一边长为a=6,另两边长b,c为方程两个根,则△ABC的周长为.
16. 关于x的方程x2﹣(3k+1)x+2k2+2k=0,若等腰三角形△ABC一边长为a=6,另两边长b,c为方程两个根,则△ABC的周长为.三、解答题
-
17. 解一元二次方程:(1)、(x﹣2)2=9;(2)、x2+2x﹣1=0.18. 解方程:(1)、x2-4x-1=0(配方法)(2)、3x(x-1)=2-2x19. 在⊙O中,AB是非直径弦,弦CD⊥AB,
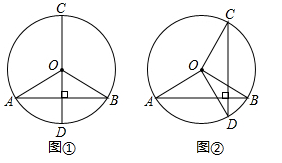 (1)、当CD经过圆心时(如图①),∠AOC+∠DOB=;(2)、当CD不经过圆心时(如图②),∠AOC+∠DOB的度数与(1)的情况相同吗?试说明你的理由.20. 已知:关于 的一元二次方程 有两个不相等的实数根.(1)、求k的取值范围;(2)、当k取最大整数值时,求该方程的解.21. 某地出土一个明代残破圆形瓷盘,为复制该瓷盘需确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心(不要求写作法、证明和讨论,但要保留作图痕迹)
(1)、当CD经过圆心时(如图①),∠AOC+∠DOB=;(2)、当CD不经过圆心时(如图②),∠AOC+∠DOB的度数与(1)的情况相同吗?试说明你的理由.20. 已知:关于 的一元二次方程 有两个不相等的实数根.(1)、求k的取值范围;(2)、当k取最大整数值时,求该方程的解.21. 某地出土一个明代残破圆形瓷盘,为复制该瓷盘需确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心(不要求写作法、证明和讨论,但要保留作图痕迹) 22. 某商店销售一款口罩,每袋的进价为12元,计划售价大于12元但不超过22元,通过试场调查发现,这种口罩每袋售价提高1元,日均销售量降低5袋,当售价为18元时,日均销售量为50袋.(1)、在售价为18元的基础上,将这种口罩的售价每袋提高x元,则日均销售量是袋;(用含x的代数式表示)(2)、要想销售这种口罩每天赢利275元,该商场每袋口罩的售价要定为多少元?23. 如图,在Rt△ABO中,∠O=90°,以点O为圆心,OB为半径的圆交AB于点C,交OA于点D.
22. 某商店销售一款口罩,每袋的进价为12元,计划售价大于12元但不超过22元,通过试场调查发现,这种口罩每袋售价提高1元,日均销售量降低5袋,当售价为18元时,日均销售量为50袋.(1)、在售价为18元的基础上,将这种口罩的售价每袋提高x元,则日均销售量是袋;(用含x的代数式表示)(2)、要想销售这种口罩每天赢利275元,该商场每袋口罩的售价要定为多少元?23. 如图,在Rt△ABO中,∠O=90°,以点O为圆心,OB为半径的圆交AB于点C,交OA于点D.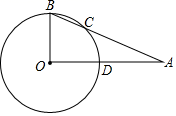 (1)、若∠A=25°,则弧BC的度数为.(2)、若OB=3,OA=4,求BC的长.24. 学校有一个面积为182平方米的长方形的活动场地,场地一边靠墙(墙长25米),另三面用长40米的合金栏网围成.请你计算一下活动场地的长和宽.
(1)、若∠A=25°,则弧BC的度数为.(2)、若OB=3,OA=4,求BC的长.24. 学校有一个面积为182平方米的长方形的活动场地,场地一边靠墙(墙长25米),另三面用长40米的合金栏网围成.请你计算一下活动场地的长和宽. 25. (阅读材料)
25. (阅读材料)把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.配方法在代数式求值、解方程、最值问题中都有着广泛的应用.
例如:①用配方法因式分解:a2+6a+8.
原式=a2+6a+9-1=(a+3) 2-1=(a+3-1)( a+3+1)=(a+2)(a+4)
②求x2+6x+11的最小值.
解:x2+6x+11=x2+6x+9+2=(x+3) 2+2;
由于(x+3) 2≥0,
所以(x+3) 2+2≥2,
即x2+6x+11的最小值为2.
请根据上述材料解决下列问题:
(1)、在横线上添上一个常数项使之成为完全平方式:a2+4a+;(2)、用配方法因式分解:a2-12a+35;(3)、用配方法因式分解:x4+4;(4)、求4x2+4x+3的最小值.26. 一轮船以每小时30km的速度由西向东航行(如图),在途中C处接到台风警报,台风中心正以每小时20km的速度从B处由南向北移动,已知距台风中心200km的区域(包括边界)都属于受台风影响区.当轮船接到台风警报时,测得BC=500km,BA=300km.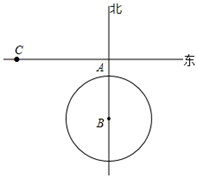 (1)、如果轮船不改变航向,轮船会不会进入台风影响区?若不会受到影响,说明理由;若会受到影响,求出受影响的时间(结果保留整数).(2)、现轮船速度减慢为每小时vkm(v<30),航向不变,在保证不受到台风影响的前提下,求v的最大值(结果保留整数).
(1)、如果轮船不改变航向,轮船会不会进入台风影响区?若不会受到影响,说明理由;若会受到影响,求出受影响的时间(结果保留整数).(2)、现轮船速度减慢为每小时vkm(v<30),航向不变,在保证不受到台风影响的前提下,求v的最大值(结果保留整数).