江苏省东台市第五联盟2021届九年级上学期数学第一次月考试卷
试卷更新日期：2020-11-06 类型：月考试卷
一、单选题
-
1. 下列方程中，关于x的一元二次方程是（ ）A、3(x＋1)2＝2(x＋1) B、 ＋ －2＝0 C、ax2＋bx＋c＝0 D、x2＋2x＝x2－12. 方程x2=9的解是（ ）A、x1=x2=3 B、x1=x2=9 C、x1=3，x2=﹣3 D、x1=9，x2=﹣93. 如图，已知A，B，C均为⊙O上的点，若∠AOB=80°，则∠ACB=（ ）
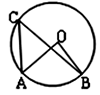A、80° B、70° C、60° D、40°4. 如图，在平面直角坐标系中，点 的坐标为（1，4）、（5，4）、（1、 ），则 外接圆的圆心坐标是（ ）
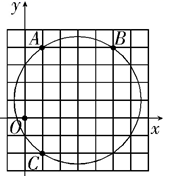A、（2，3） B、（3，2） C、（1，3） D、（3，1）5. 如图，已知在⊙O中，AB是弦，半径OC⊥AB，垂足为点D，要使四边形OACB为菱形，还需要添加一个条件，这个条件可以是（ ）
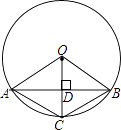A、AD=BD B、OC=2CD C、∠CAD=∠CBD D、∠OCA=∠OCB6.如图，某小区计划在一块长为32m，宽为20m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m2 ． 若设道路的宽为xm，则下面所列方程正确的是（ ）
A、（32﹣2x）（20﹣x）=570 B、32x+2×20x=32×20﹣570 C、（32﹣x）（20﹣x）=32×20﹣570 D、32x+2×20x﹣2x2=5707. 如图，已知⊙O的半径为5，弦AB长度为8，则⊙O上到弦AB所在直线的距离为2的点有（ ）个．
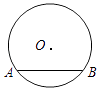A、1 B、2 C、3 D、48. 如图，AB是⊙O的直径，点C在⊙O上，AE是⊙O的切线，A为切点，连接BC并延长交AE于点D.若 ∠AOC=80°，则 ∠ADB的度数为（ ）
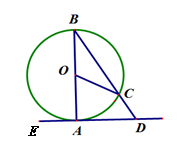A、40° B、50° C、60° D、20°二、填空题
-
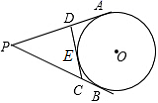
9. 一元二次方程x2﹣2x=0的解是 ．10. 关于x的一元二次方程kx2﹣4x﹣ ＝0有实数根，则k的取值范围是.11. 当 时，代数式 比代数式 的值大2.12. 如图，PA，PB分别切⊙O于A，B，并与⊙O的切线，分别相交于C，D，已知△PCD的周长等于10cm，则PA= cm.
13.如图，在△ABC中，AB=AC ， ∠B=30°，以点A为圆心，以3cm为半径作⊙A ， 当AB=cm时，BC与⊙A相切．
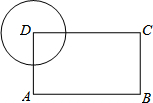
14. 已知⊙O的半径2，则其内接正三角形的面积为 ．15.如图，在矩形ABCD中，AB=4，AD=3，以顶点D为圆心作半径为r的圆，若要求另外三个顶点A、B、C中至少有一个点在圆内，且至少有一个点在圆外，则r的取值范围是 ．
16. 在Rt△ABC中，∠C=90°，BC=3，AC=4，点P在以C为圆心，5为半径的圆上，连结PA，PB．若PB=4，则PA的长为 ．三、解答题
-
17. 解下列方程：(1)、（x﹣3）2=2（x﹣3）(2)、x2-4x+1=0（用配方法）；18. 已知关于
的方程 
.
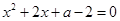(1)、若该方程有两个不相等的实数根，求实数
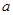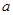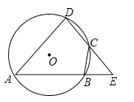
的取值范围； (2)、若该方程的一个根为1，求 的值及该方程的另一根． 19. 已知某等腰三角形的腰和底分别是一元二次方程x2﹣6x+5=0的两根，求此三角形的周长.20.如图，已知A、B、C、D是⊙O上的四点，延长DC、AB相交于点E．若BC=BE．求证：△ADE是等腰三角形．
21. 如图，要建一个面积为45 m2的长方形养鸡场(分为两片)，养鸡场的一边靠着一面长为14m的墙，另几条边用总长为22 m的竹篱笆围成，每片养鸡场的前面各开一个宽l m的门.求这个养鸡场的长与宽.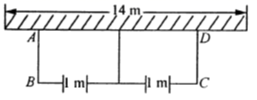
22. 如图，在△ABC中，∠CAB＝90°，∠CBA＝50°，以AB为直径作⊙O交BC于点D，点E在边AC上，且满足ED＝EA.
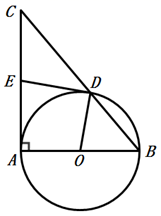(1)、求∠DOA的度数；(2)、求证：直线ED与⊙O相切.23. 如图，要把残破的轮片复制完整，已知弧上的三点A、B、C.
(1)、用尺规作图法找出 所在圆的圆心(保留作图痕迹，不写作法)；(2)、设△ABC是等腰三角形，底边BC＝8cm，腰AB＝5cm，求圆片的半径R.24. 如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作⊙O的切线DF，交AC于点F.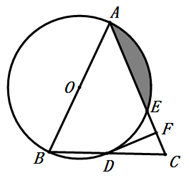
(1)、求证：DF⊥AC；(2)、若⊙O的半径为4，∠C=67.5°，求阴影部分的面积.25. 2017年中秋节来期间，某超市以每盒80元的价格购进了1000盒月饼，第一周以每盒168元的价格销售了300盒，第二周如果单价不变，预计仍可售出300盒，该超市经理为了增加销量，决定降价，据调查，单价每降低1元，可多售出10盒，但最低每盒要赢利30元，第二周结束后，该超市将对剩余的月饼一次性赔钱甩卖，此时价格为70元/盒．
(1)、若设第二周单价降低x元，则第二周的单价是 ， 销量是 ；
(2)、经两周后还剩余月饼 盒；(3)、若该超市想通过销售这批月饼获利51360元，那么第二周的单价应是多元？
26. 如图，⊙O的半径为1，A，P，B，C是⊙O上的四个点.∠APC=∠CPB=60°.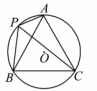
(1)、判断△ABC的形状：；(2)、试探究线段PA，PB，PC之间的数量关系，并证明你的结论；(3)、当点P位于 的什么位置时，四边形APBC的面积最大？求出最大面积.27. 如图，四边形ABCD为菱形，对角线AC，BD相交于点E，F是边BA延长线上一点，连接EF，以EF为直径作⊙O，交DC于D，G两点，AD分别与EF，GF交于I，H两点.
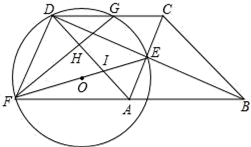(1)、求∠FDE的度数；(2)、试判断四边形FACD的形状，并证明你的结论；(3)、当G为线段DC的中点时，①求证：FD=FI；
②设AC=2m，BD=2n，求m：n的值.