广东省揭阳市揭西县2020-2021学年九年级上学期数学第一次月考试卷
试卷更新日期:2020-11-05 类型:月考试卷
一、单选题
-
1. 小明和小颖做“剪刀、石头、布”的游戏,假设他们每次出这三种手势的可能性相同,则在一次游戏中两人手势相同的概率是( )A、 B、 C、 D、2. 若 = ,则下列各式不成立的是( )A、 = B、 = C、 = D、 =3. 下列条件中,能判定▱ABCD是菱形的是( )A、AC=BD B、AB⊥BC C、AD=BD D、AC⊥BD4. 已知关于x的方程x2﹣x+m=0的一个根是3,则另一个根是( )A、﹣6 B、6 C、﹣2 D、25. 身高1.6米的小明同学利用相似三角形测量学校旗杆的高度,上午10点,小明在阳光下的影长为1米,此时测得旗杆的影长为9米,则学校旗杆的高度是( )A、 米 B、 米 C、 米 D、 米6. 在一个不透明的布袋中装有60个白球和若干个黑球,除颜色外其他都相同,小红每次摸出一个球并放回,通过多次试验后发现,摸到黑球的频率稳定在0.6左右,则布袋中黑球的个数可能有( )A、24 B、36 C、40 D、907. 如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标分别为( )
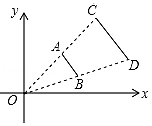 A、(4,4) B、(3,3) C、(3,1) D、(4,1)8. 如图,在矩形 中, , ,点E在边CD上,且 .连接BE,将 沿 折叠,点C的对应点 恰好落在边 上,则m=( )
A、(4,4) B、(3,3) C、(3,1) D、(4,1)8. 如图,在矩形 中, , ,点E在边CD上,且 .连接BE,将 沿 折叠,点C的对应点 恰好落在边 上,则m=( )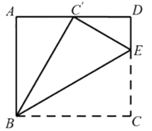 A、 B、 C、 D、49. 已知m,n是一元二次方程x2=x的两个实数根,则下列结论错误的是( )A、m+n=0 B、m•n=0 C、m2=m D、n2=n10. 如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A、 B、 C、 D、49. 已知m,n是一元二次方程x2=x的两个实数根,则下列结论错误的是( )A、m+n=0 B、m•n=0 C、m2=m D、n2=n10. 如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )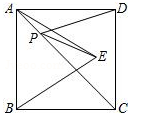 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在 中,点E是 的中点, , 的延长线交于点F.若 的面积为1,则四边形 的面积为.
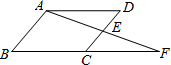 12. 现有四张正面分别标有数字﹣1,1,2,3的不透明卡片,它们除数字外其余完全相同,将它们背而面朝上洗均匀,随机抽取一张,记下数字后放回 , 背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为m , n , 则点P(m , n)在第二象限的概率为 .13. 如图,在矩形ABCD中,AB=6,对角线AC与BD相交于点O,AE⊥BD,垂足为E,若BE=EO,则AD的长是.
12. 现有四张正面分别标有数字﹣1,1,2,3的不透明卡片,它们除数字外其余完全相同,将它们背而面朝上洗均匀,随机抽取一张,记下数字后放回 , 背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为m , n , 则点P(m , n)在第二象限的概率为 .13. 如图,在矩形ABCD中,AB=6,对角线AC与BD相交于点O,AE⊥BD,垂足为E,若BE=EO,则AD的长是.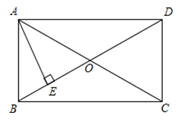 14. 若关于x的一元二次方程 有两个实数根,则k的取值范围是 .15. 如图,在△ABC中,D为AC边上的中点,AE∥BC,ED交AB于G,交BC延长线于F.若BG:GA=3:1,BC=10,则AE的长为 .
14. 若关于x的一元二次方程 有两个实数根,则k的取值范围是 .15. 如图,在△ABC中,D为AC边上的中点,AE∥BC,ED交AB于G,交BC延长线于F.若BG:GA=3:1,BC=10,则AE的长为 .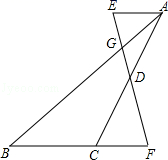 16. 如图,将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计).若长方形纸板边长分别为40cm和30cm , 且折成的长方体盒子表面积是950cm2 , 此时长方体盒子的体积为cm3 .
16. 如图,将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计).若长方形纸板边长分别为40cm和30cm , 且折成的长方体盒子表面积是950cm2 , 此时长方体盒子的体积为cm3 .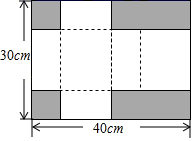 17. 已知平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上且坐标是(0,2),点C1、E1、E2、C2、E3、E4、C3在x轴上,C1的坐标是(1,0).B1C1∥B2C2∥B3C3 , 以此继续下去,则点A2020到x轴的距离是.
17. 已知平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上且坐标是(0,2),点C1、E1、E2、C2、E3、E4、C3在x轴上,C1的坐标是(1,0).B1C1∥B2C2∥B3C3 , 以此继续下去,则点A2020到x轴的距离是.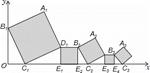
三、解答题
-
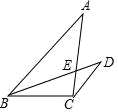
18. 解方程(1)、x2-5x=0(2)、(x-3)(x+3)=2x19. 如图,在△ABC中,AB=8,BC=4,CA=6,CD//AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.
 20. 平行四边形 ABCD中,过点D作DE⊥AB于点E,点F在CD上,DF=BE,连接:BF,AF.
20. 平行四边形 ABCD中,过点D作DE⊥AB于点E,点F在CD上,DF=BE,连接:BF,AF.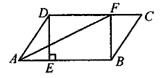 (1)、求证:四边形BFDE是矩形;(2)、若AF平分∠BAD,且AE=3,DF=5,求矩形BFDE的面积.21. 2020年突如其来的新型冠状病毒疫情,给生鲜电商带来了意想不到的流量和机遇,据统计某生鲜电商平台1月份的销售额是1440万元,3月份的销售额是2250万元.(1)、若该平台1月份到3月份的月平均增长率都相同,求月平均增长率是多少?(2)、市场调查发现,某水果在“盒马鲜生”平台上的售价为20元/千克时,每天能销售200千克,售价每降价2元,每天可多售出100千克,为了推广宣传,商家决定降价促销,同时尽量减少库存,已知该水果的成本价为12元/千克,若使销售该水果每天获利1750元,则售价应降低多少元?22. 将4张印有“梅”“兰”“竹”“菊”字样的卡片(卡片的形状、大小、质地都相同)放在一个不透明的盒子中,将卡片搅匀.(1)、从盒子中任意取出1张卡片,恰好取出印有“兰”字的卡片的概率为.(2)、先从盒子中任意取出1张卡片,记录后放回并搅匀,再从中任意取出1张卡片,求取出的两张卡片中,至少有1张印有“兰”字的概率(请用画树状图或列表等方法求解).23. 如图,矩形 中, , ,点 在 上,连接 点 在直线 上, 交 于点 .
(1)、求证:四边形BFDE是矩形;(2)、若AF平分∠BAD,且AE=3,DF=5,求矩形BFDE的面积.21. 2020年突如其来的新型冠状病毒疫情,给生鲜电商带来了意想不到的流量和机遇,据统计某生鲜电商平台1月份的销售额是1440万元,3月份的销售额是2250万元.(1)、若该平台1月份到3月份的月平均增长率都相同,求月平均增长率是多少?(2)、市场调查发现,某水果在“盒马鲜生”平台上的售价为20元/千克时,每天能销售200千克,售价每降价2元,每天可多售出100千克,为了推广宣传,商家决定降价促销,同时尽量减少库存,已知该水果的成本价为12元/千克,若使销售该水果每天获利1750元,则售价应降低多少元?22. 将4张印有“梅”“兰”“竹”“菊”字样的卡片(卡片的形状、大小、质地都相同)放在一个不透明的盒子中,将卡片搅匀.(1)、从盒子中任意取出1张卡片,恰好取出印有“兰”字的卡片的概率为.(2)、先从盒子中任意取出1张卡片,记录后放回并搅匀,再从中任意取出1张卡片,求取出的两张卡片中,至少有1张印有“兰”字的概率(请用画树状图或列表等方法求解).23. 如图,矩形 中, , ,点 在 上,连接 点 在直线 上, 交 于点 .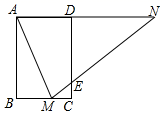 (1)、求证: 是等腰三角形;(2)、求证: ;(3)、当 为 中点时,求 的长.24. 如图,在矩形ABCD中,AD=kAB(k>0),点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F.
(1)、求证: 是等腰三角形;(2)、求证: ;(3)、当 为 中点时,求 的长.24. 如图,在矩形ABCD中,AD=kAB(k>0),点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F.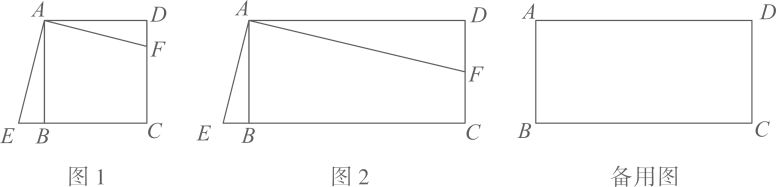 (1)、如图1,若k=1,则AF与AE之间的数量关系是;(2)、如图2,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示)(3)、若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,求EG的长.25. 如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.
(1)、如图1,若k=1,则AF与AE之间的数量关系是;(2)、如图2,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示)(3)、若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,求EG的长.25. 如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.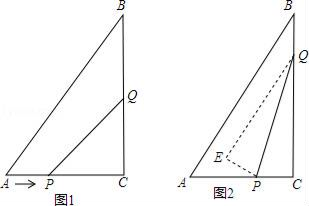 (1)、当t=2时,求线段PQ的长度;(2)、当t为何值时,△PCQ的面积等于5cm2?(3)、在P、Q运动过程中,在某一时刻,若将△PQC翻折,得到△EPQ,如图2,PE与AB能否垂直?若能,求出相应的t值;若不能,请说明理由.
(1)、当t=2时,求线段PQ的长度;(2)、当t为何值时,△PCQ的面积等于5cm2?(3)、在P、Q运动过程中,在某一时刻,若将△PQC翻折,得到△EPQ,如图2,PE与AB能否垂直?若能,求出相应的t值;若不能,请说明理由.