安徽省亳州市2020-2021学年九年级上学期数学第一次月考试卷
试卷更新日期:2020-11-05 类型:月考试卷
一、单选题
-
1. 抛物线y=(x﹣3)2﹣5的顶点坐标是( )A、(3,5) B、(﹣3,5) C、(3,﹣5) D、(﹣3,﹣5)2. 如图,抛物线 与y轴交于点C,点D在抛物线上,且 轴,则线段CD的长为( ).
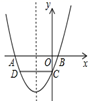 A、2 B、3 C、4 D、53. 关于二次函数 ,下列说法正确的是( )A、当x<1时,y值随x值的增大而增大 B、当x<1时,y值随x值的增大而减小 C、当 时,y值随x值的增大而增大 D、当 时,y值随x值的增大而减小4. 抛物线 ,如图所示,则函数y的最小值和最大值分别是( )
A、2 B、3 C、4 D、53. 关于二次函数 ,下列说法正确的是( )A、当x<1时,y值随x值的增大而增大 B、当x<1时,y值随x值的增大而减小 C、当 时,y值随x值的增大而增大 D、当 时,y值随x值的增大而减小4. 抛物线 ,如图所示,则函数y的最小值和最大值分别是( )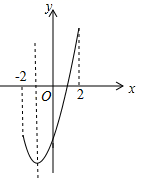 A、-3和5 B、-4和5 C、-4和-3 D、-1和55. 二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)的图象如图所示,下列结论错误的是( )
A、-3和5 B、-4和5 C、-4和-3 D、-1和55. 二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)的图象如图所示,下列结论错误的是( )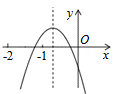 A、a<0 B、b<0 C、c<0 D、a<b6. 在同一坐标系内,函数y=kx2和y=kx+2(k≠0)的图象大致如图( )A、
A、a<0 B、b<0 C、c<0 D、a<b6. 在同一坐标系内,函数y=kx2和y=kx+2(k≠0)的图象大致如图( )A、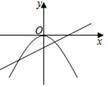 B、
B、 C、
C、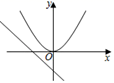 D、
D、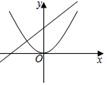 7. 在平面直角坐标系中,抛物线y=(x+3)(x﹣1)经过变换后得到抛物线y=(x+1)(x﹣3),则这个变换可以是( )A、向左平移2个单位 B、向右平移2个单位 C、向左平移4个单位 D、向右平移4个单位8. k为任意实数,抛物线y=a(x﹣k)2﹣k(a≠0)的顶点总在( )A、直线y=x上 B、直线y=﹣x上 C、x轴上 D、y轴上9. 如图,某幢建筑物从2.25米高的窗口A用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面3米,则水流下落点B离墙的距离OB是( )
7. 在平面直角坐标系中,抛物线y=(x+3)(x﹣1)经过变换后得到抛物线y=(x+1)(x﹣3),则这个变换可以是( )A、向左平移2个单位 B、向右平移2个单位 C、向左平移4个单位 D、向右平移4个单位8. k为任意实数,抛物线y=a(x﹣k)2﹣k(a≠0)的顶点总在( )A、直线y=x上 B、直线y=﹣x上 C、x轴上 D、y轴上9. 如图,某幢建筑物从2.25米高的窗口A用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面3米,则水流下落点B离墙的距离OB是( )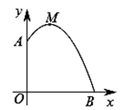 A、2.5米 B、3米 C、3.5米 D、4米10. 定义:在平面直角坐标系中,过一点P分别作坐标轴的垂线,这两条垂线与坐标轴围成一个矩形,若矩形的周长值与面积值相等,则点P叫作和谐点,所围成的矩形叫作和谐矩形.已知点P是抛物线 上的和谐点,所围成的和谐矩形的面积为16,则k的值可以是( )A、16 B、4 C、 12 D、 18
A、2.5米 B、3米 C、3.5米 D、4米10. 定义:在平面直角坐标系中,过一点P分别作坐标轴的垂线,这两条垂线与坐标轴围成一个矩形,若矩形的周长值与面积值相等,则点P叫作和谐点,所围成的矩形叫作和谐矩形.已知点P是抛物线 上的和谐点,所围成的和谐矩形的面积为16,则k的值可以是( )A、16 B、4 C、 12 D、 18二、填空题
-
11. 当x=0时,函数 有最小值1,则b-c= .12. 直线 与抛物线 如图所示,当 > 时,x的取值范围是 .
 13. 关于x的函数 是二次函数,则m= .14. 如图,点O为坐标原点,点C , F都在y轴正半轴上,点M为OC中点,四边形OABC和CDEF都是正方形,抛物线 经过M , B , E三点.
13. 关于x的函数 是二次函数,则m= .14. 如图,点O为坐标原点,点C , F都在y轴正半轴上,点M为OC中点,四边形OABC和CDEF都是正方形,抛物线 经过M , B , E三点.⑴当b=1时,a=;
⑵ 的值为 .

三、解答题
-
15. 已知点 在以y轴为对称轴的抛物线 上,求 的最大值.16. 在二次函数 中,y与x的部分对应值如下表:
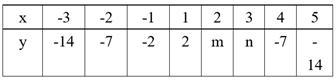
试判断m , n的大小关系.
17. 如图,已知点 ,点 ,抛物线 (h , k均为常数)与线段AB交于C , D两点,且 ,求k的值.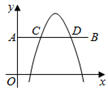 18. 已知函数 ,(1)、将此函数化为 的形式,则h= , k=;(2)、在所给平面直角坐标系中画出该函数的大致图象.
18. 已知函数 ,(1)、将此函数化为 的形式,则h= , k=;(2)、在所给平面直角坐标系中画出该函数的大致图象.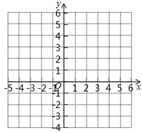 19. 已知抛物线 与y轴交于点 ,点D和点C关于抛物线的对称轴对称.(1)、直接写出:m= , 点D的坐标是;(2)、如果点M是抛物线的对称轴与x轴的交点,求△MCD的周长.20. 如图,抛物线 与y=4交于A , B两点,与x轴交于C , D两点,分别连接AC , AD , BC , 点B关于直线AC的对称点恰好落在线段OC上.
19. 已知抛物线 与y轴交于点 ,点D和点C关于抛物线的对称轴对称.(1)、直接写出:m= , 点D的坐标是;(2)、如果点M是抛物线的对称轴与x轴的交点,求△MCD的周长.20. 如图,抛物线 与y=4交于A , B两点,与x轴交于C , D两点,分别连接AC , AD , BC , 点B关于直线AC的对称点恰好落在线段OC上.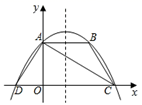 (1)、求证:AB=AD;(2)、求a的值.21. 如图,二次函数 的图像过点 和 ,对称轴为直线x=1.
(1)、求证:AB=AD;(2)、求a的值.21. 如图,二次函数 的图像过点 和 ,对称轴为直线x=1.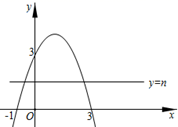 (1)、求二次函数G1的解析式;(2)、当 时,求函数G1中y的取值范围;(3)、当直线y=n与 的图象共有4个公共点时,直接写出n的取值范围.22. 在平面直角坐标系中,已知抛物线y=x2﹣2ax+4a+2(a是常数),(1)、若该抛物线与x轴的一个交点为(﹣1,0),求a的值及该抛物线与x轴另一交点坐标;(2)、不论a取何实数,该抛物线都经过定点H .
(1)、求二次函数G1的解析式;(2)、当 时,求函数G1中y的取值范围;(3)、当直线y=n与 的图象共有4个公共点时,直接写出n的取值范围.22. 在平面直角坐标系中,已知抛物线y=x2﹣2ax+4a+2(a是常数),(1)、若该抛物线与x轴的一个交点为(﹣1,0),求a的值及该抛物线与x轴另一交点坐标;(2)、不论a取何实数,该抛物线都经过定点H .①求点H的坐标;
②证明点H是所有抛物线顶点中纵坐标最大的点.
23. 亳州市某超市经销某种特色水果的成本为每千克20元,在一段时间内,销售单价P(元/kg)与时间t(天)的函数图象如图,且其日销售量y(kg)与时间t(天)的关系是: (其中天数t为整数)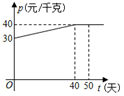 (1)、当0≤t≤40天,求销售单价p(元/kg)与时间t(天)之间的函数关系式;(2)、问哪一天的销售利润最大?最大日销售利润为多少?(3)、在前20天中,超市决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫“对象,而且每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
(1)、当0≤t≤40天,求销售单价p(元/kg)与时间t(天)之间的函数关系式;(2)、问哪一天的销售利润最大?最大日销售利润为多少?(3)、在前20天中,超市决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫“对象,而且每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.