安徽省合肥市庐江县2020-2021学年八年级上学期数学第一次月考试卷
试卷更新日期：2020-11-05 类型：月考试卷
一、单选题
-
1. 在直角三角形ABC中，∠A：∠B：∠C＝2：m：4，则m的值是（ ）A、3 B、4 C、2或6 D、2或42. 如图，将△ABC纸片沿DE进行折叠，使点A落在四边形BCED的外部点A’的位置，若∠A=35°，则∠1-∠2的度数为（ ）
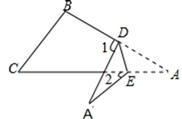A、35° B、70° C、55° D、40°3. 如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到C的方向平移到△DEF的位置，AB=10，DO=4，平移距离为6，则阴影部分面积为（ ）
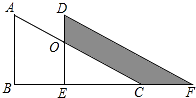A、48 B、96 C、84 D、424. 如图，AD是 中∠BAC的平分线，DE⊥AB交AB于点E ， DF⊥AC交AC于点F ， 若 ，DE＝2，AB＝4，则AC的长为（ ）
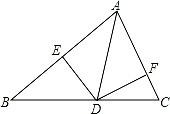A、3 B、4 C、5 D、65. 工人师傅常用角尺平分一个任意角，做法如下：如图，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，移动角尺，使角尺两边相同的到刻度分别与点M、N重合，过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC，其依据是（ ）
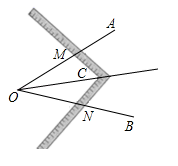A、SSS B、SAS C、ASA D、AAS6. 如图，四边形ABCD中，∠A＝90°，AD＝2，连接BD ， BD⊥CD ， 垂足是D且∠ADB＝∠C ， 点P是边BC上的一动点，则DP的最小值是（ ）
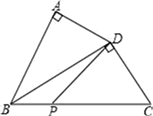A、1 B、1.5 C、2 D、2.57. 如图，在 中，AC边上的高是（ ）
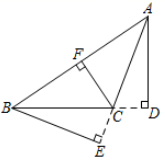A、BE B、AD C、CF D、AF8. 长度分别为1，5，x的三条线段首位连接能组成一个三角形，则x的值可以是（ ）A、4 B、5 C、6 D、79. 如图，△ABC中，AB＝AC，D、E分别在CA、BA的延长线上，连接BD、CE，且∠D＋∠E＝180°，若BD＝6，则CE的长为（ ）
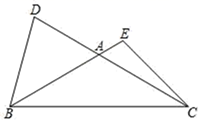A、6 B、5 C、3 D、4.510. 如图，CD、BD分别平分∠ACE、∠ABC ， ∠A＝70°，则∠BDC＝（ ）
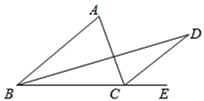A、35° B、25° C、70° D、60°二、填空题
-
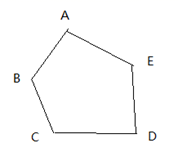
11. 从如图的五边形ABCDE纸片中减去一个三角形，剩余部分的多边形的内角和是
12. 如图，OP平分∠AOB ， PM⊥OA于M ， 点D在OB上，DH⊥OP于H ． 若OD＝4，OP＝7，PM＝3，则DH的长为 ．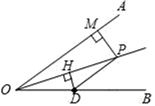
13. 一个锐角三角形，所有内角的度数均为正整数，且最小角是最大角的 ，则这个锐角三角形三个内角的度数为 ．14. 如图，两根旗杆间相距20米，某人从点B沿BA走向点A ， 一段时间后他到达点M ， 此时他分别仰望旗杆的顶点C和D ， 两次视线的夹角为90°，且CM＝DM ． 已知旗杆BD的高为12米，该人的运动速度为2米/秒，则这个人运动到点M所用时间是秒．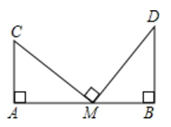
三、解答题
-
15. 若a，b，c是△ABC三边的长，化简：|a+b-c|+|b-a-c|-|c-a-b|．16. 已知三角形的两边 ，若第三边 的长为偶数，求其周长.17. 如图，点A，F，E，D在一条直线上，AB＝CD，AF＝DE，∠BAE＝∠CDF．求证：BE=CF．
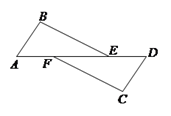18. 如图，四边形ABCD中，∠A＝∠C＝90°，若AB＝BC ． 求证：BD平分∠ABC ．
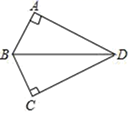19. 已知：AB＝AC ， BE＝CD ．
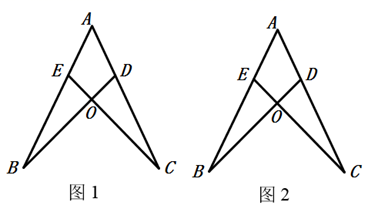(1)、如图1，求证：∠B＝∠C；(2)、如图2，连接AO ， 不添加任何辅助线，直接写出图中所有的全等三角形．20. 在四边形ABCD中，E为BC边中点．已知：如图，若AE平分∠BAD ， ∠AED＝90°，点F为AD上一点，AF＝AB ．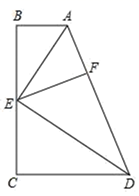
求证：
(1)、△ABE≌AFE；(2)、AD＝AB+CD；21. （探究）如图①，在△ABC中，∠ABC的平分线与∠ACB的平分线相交于点P ．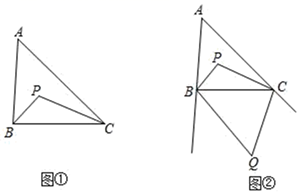
(1)、若∠ABC＝80°，∠ACB＝50°．则∠A＝度，∠P＝度．(2)、∠A与∠P的数量关系，并说明理由．(3)、（应用）如图②，在△ABC中，∠ABC的平分线与∠ACB的平分线相交于点P ． ∠ABC的外角平分线与∠ACB的外角平分线相交于点Q ． 直接写出∠A与∠Q的数量关系为 ．22. 现有一张△ABC纸片，点D、E分别是△ABC边上两点，若沿直线DE折叠．
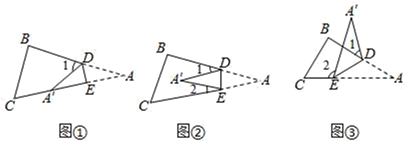(1)、如果折成图①的形状，使点A落在CE上，则∠1与∠A的数量关系是 ．(2)、如果折成图②的形状，猜想∠1+∠2与∠A的数量关系是；(3)、如果折成图③的形状，猜想∠1、∠2和∠A的数量关系，并说明理由．23. 如图，在△ABC中，AB=AC=18cm，BC=10cm，AD=2BD．
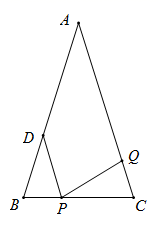(1)、如果点P在线段BC上以2cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．①若点Q的运动速度与点P的运动速度相等，经过2s后，△BPD与△CQP是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
(2)、若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？