安徽合肥市三十八中2020-2021学年八年级上学期数学第一次月考试卷

试卷更新日期：2020-11-05 类型：月考试卷

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点 $(2, - 1)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下面哪个点在函数y=2x-1的图像上（）

A、(1，1) B、(0，1) C、(-1，0) D、(3，2)

查看试题解析
3. 看一次函数y=（3-k）x-k的图象经过第一、三、四象限，则k的取值范围是（）

A、k>3 B、0<k<3 C、k<0 D、k<3

查看试题解析
4. 已知一次函数的图象与直线y=-2x+1平行，且过点(8，2)那么此一次函数的解析式为（）

A、y=2x-14 B、y=-2x+18 C、y=4x D、y=-2x+12

查看试题解析
5. 下列函数中，自变量x的取值范围是x≥2的是（）

A、 $y = \sqrt{2 - x}$ B、 $y = \frac{1}{\sqrt{x - 2}}$ C、 $y = \sqrt{x + 2} + \sqrt{x - 2}$ D、 $y = \frac{1}{x - 2}$

查看试题解析
6. P₁(x₁ ， y₁)，P₂(x₂ ， y₂)在一次函数 $y = \sqrt{3} x - 2$ ．下列判断正确的是（）

A、y₁> y₂ B、y₁< y₂ C、当x₁< x₂时，y₁> y₂ D、当x₁< x₂时，y₁< y₂

查看试题解析
7. 要从 $y = \frac{4}{3} x$ 的图象得到直线 $y = \frac{4 x + 2}{3}$ ，则要将直线 $y = \frac{4}{3} x$ （）

A、向上平移2个单位 B、向上平移 $\frac{2}{3}$ 个单位 C、向下平移2个单位 D、向下平移 $\frac{2}{3}$ 个单位

查看试题解析
8. A (x₁ ， y)，B(x₂ ， y₂)是一次函数y=kx+2（k>0）图像上的不同的两点，若t=（x₁- x₂）（y₁-y₂），则（）

A、t<1 B、t>0 C、t=0 D、t≤1

查看试题解析
9. 如图，是在同一坐标系内作出的一条函数的图象l₁ ， l₂ ，设y=k₁x+b₁ ， y=k₂x+b₂ ，则方程组 ${_{y = k_{2} x + b_{2}}^{y = k_{1} x + b_{1}}$ 的解是（）．

A、 ${_{y = 2}^{x = - 2}$ B、 ${_{y = 3}^{x = - 3}$ C、 ${_{y = 3}^{x = - 2}$ D、不能确定

查看试题解析
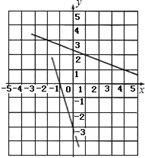10. 如图，点B、C分别在直线y=2x和y=kx上，点A、D是x轴上的两点，已知四边形ABCD是正方形，则k的值为（）

A、 $\frac{2}{3}$ B、1 C、 $\frac{3}{2}$ D、不能确定

查看试题解析

二、填空题

11. 直线y=-3x+1不经过第象限

查看试题解析
12. y=（m-3）x+m²-9 是正比例函数，则m=

查看试题解析
13. 点P到x轴的距离是3，到y轴的距离是5，且在y轴的左侧，则P点的坐标是

查看试题解析
14. 已知一次函数y=2x-a与y=3x+b的图象交于x轴上原点外的一点，则 $\frac{a}{a + b}$ =.

查看试题解析

三、解答题

15. 已知一次函数y=kx+b的图像经过点(-2，-4)，且与正比例函数 $y = \frac{1}{2} x$ 的图像相交于点(4，a )，求：

(1)、a的值；

(2)、k、b的值

查看试题解析
16. 一次函数y=kx+b的图像如图所示：

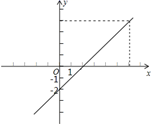(1)、求出该一次函数的表达式；

(2)、求当x=9时，y的值；

(3)、求当y=3时，x的值；

查看试题解析
17. 已知函数y=（2n-8）x-n-3

(1)、若函数图象经过原点，求n的值

(2)、若这个函数是一次函数，且图像经过二、三、四象限，求n的正整数值

查看试题解析
18. 在某地，人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系，下面是蟋蟀所叫次数与温度变化情况对照表：

蟋蟀叫次数

…

84

98

119

…

温度（℃）

…

15

17

20

…

(1)、根据表中数据确定该一次函数的关系式；

(2)、如果蟋蟀1分钟叫了63次，那么该地当时的温度大约为多少摄氏度？

查看试题解析
19. 如图，四边形ABCD各个顶点的坐标分别为(-2，8)、(-11，6)、(-14，0)、(0，0)，求这个四边形的面积

查看试题解析
20. 如图，直线l的解析式为y=-x+6，它与x轴，y轴分别交于A、B两点，平行于直线l的直线m，从原点O出发，沿x轴的正方向以每秒1个单位长度的速度运动，它与x轴、y轴分别交于M、N两点，设运动时间为t秒（0＜t≤4）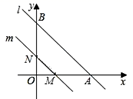

(1)、求A、B两点的坐标；

(2)、用含t的代数式表示 $△ M O N$ 的面积S

查看试题解析
21. 画出函数y＝－4x＋8图像
⑴利用图像求不等式－4x＋8＞0的解集；

⑵利用图像求不等式－4x＋8≤4的解集

⑶如果y值在－4≤y＜8的范围内，求相应的x的取值范围．

查看试题解析
22. 如图，直线 $y = \frac{1}{2} x + 4$ 与x轴、y轴分别交于A、B两点，点C的的坐标为(-6，0)，点P(x，y)是直线 $y = \frac{1}{2} x + 4$ 上的一个动点（点P不与点A重合）．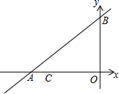

(1)、在点P的运动过程，试写出△OPC的面积S与x之间的函数关系式

(2)、当点P运动到什么位置时，△OPC的面积为15？求出此时点P的坐标

查看试题解析
23. 某商场筹集资金12.8万元，一次性购进空调、彩电共30台，根据市场需要，这些空调，彩电可以全部销售，计划全部销售后利润不少于2.25万元，其中空调，彩电的进价和售价见表格：

空调

彩电

进价（元/台）

5000

3200

售价（元/台）

5800

3900

设商场计划购进空调x台

(1)、空调和彩电全部销售后商场获得的利润为y元，求出y与x的函数关系式；

(2)、商场有哪几种进货方案可供选择？

(3)、由于商场的空调进行了促销活动，实际空调获利只有计划的80%，按原计划的哪个进货方案，商场获利最大？最大利润是多少元？

查看试题解析

	空调	彩电
进价（元/台）	5000	3200
售价（元/台）	5800	3900

蟋蟀叫次数	…	84	98	119	…
温度（℃）	…	15	17	20	…