天津市河北区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-05 类型:期末考试
一、单选题
-
1. 下列四个图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件是随机事件的是( )A、随意掷一块质地均匀的骰子,掷出的点数是奇数 B、在一个标准大气压下,把水加热到100℃,水就会沸腾 C、有一名运动员奔跑的速度是80米/秒 D、在一个仅装着白球和黑球的袋中摸球,摸出红球3. 若双曲线 的图象的一支位于第三象限,则k的取值范围是( )A、k<1 B、k>1 C、0<k<1 D、k≤14. 关于x的一元二次方程 有两个不相等的实数根,则k的取值范围是A、 B、 C、 且 D、 且5. 如图,在△ABC中,DE∥BC, , DE=4,则BC的长是( )
2. 下列事件是随机事件的是( )A、随意掷一块质地均匀的骰子,掷出的点数是奇数 B、在一个标准大气压下,把水加热到100℃,水就会沸腾 C、有一名运动员奔跑的速度是80米/秒 D、在一个仅装着白球和黑球的袋中摸球,摸出红球3. 若双曲线 的图象的一支位于第三象限,则k的取值范围是( )A、k<1 B、k>1 C、0<k<1 D、k≤14. 关于x的一元二次方程 有两个不相等的实数根,则k的取值范围是A、 B、 C、 且 D、 且5. 如图,在△ABC中,DE∥BC, , DE=4,则BC的长是( ) A、8 B、10 C、11 D、126. 如图,平面直角坐标系中,点E(﹣4,2),F(﹣1,﹣1),以原点O为位似中心,把△EFO缩小为△E′F′O , 且△E′F′O与△EFO的相似比为1:2,则点E的对应点E′的坐标为( )
A、8 B、10 C、11 D、126. 如图,平面直角坐标系中,点E(﹣4,2),F(﹣1,﹣1),以原点O为位似中心,把△EFO缩小为△E′F′O , 且△E′F′O与△EFO的相似比为1:2,则点E的对应点E′的坐标为( )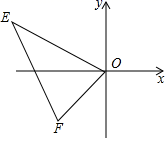 A、(2,﹣1) B、(8,﹣4) C、(2,﹣1)或(﹣2,1) D、(8,﹣4)或(﹣8,4)7. 正六边形的半径与边心距之比为( )A、1: B、 :1 C、 :2 D、2:8. 在一次同学聚会上,每人都向其他人赠送了一份小礼品,共互送110份小礼品,如果参加聚会的同学有x名.根据题意列出的方程是( )。A、x (x + 1) = 110 B、x (x -1) = 110 C、2x ( x + 1) = 110 D、x (x-1) = 110×29. 已知△ABC中,∠C=90°,BC=a,CA=b,AB=c,⊙O与三角形的边相切,下列选项中,⊙O的半径为 的是( )A、
A、(2,﹣1) B、(8,﹣4) C、(2,﹣1)或(﹣2,1) D、(8,﹣4)或(﹣8,4)7. 正六边形的半径与边心距之比为( )A、1: B、 :1 C、 :2 D、2:8. 在一次同学聚会上,每人都向其他人赠送了一份小礼品,共互送110份小礼品,如果参加聚会的同学有x名.根据题意列出的方程是( )。A、x (x + 1) = 110 B、x (x -1) = 110 C、2x ( x + 1) = 110 D、x (x-1) = 110×29. 已知△ABC中,∠C=90°,BC=a,CA=b,AB=c,⊙O与三角形的边相切,下列选项中,⊙O的半径为 的是( )A、 B、
B、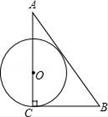 C、
C、 D、
D、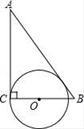 10. 如图,抛物线y=ax2+bx+c(a , b , c是常数,a≠0)与x轴交于A , B两点,顶点P(m , n).给出下列结论
10. 如图,抛物线y=ax2+bx+c(a , b , c是常数,a≠0)与x轴交于A , B两点,顶点P(m , n).给出下列结论①2a+c>0;
②若 在抛物线上,则y1>y2>y3
③关于x的方程ax2+bx+k=0有实数解,则k>c﹣n;
④当n=﹣ 时,△ABP为等腰直角三角形;
其中符合题意结论个数有( )个.
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 抛物线 与 轴有个交点.12. 如果二次函数 (m为常数)的图象有最高点,那么m的值为 .13. 如图,四边形ABCD内接于⊙O , E为CD延长线上一点,若∠B=100°,则∠ADE= .
 14. 两个相似三角形对应边上的中线之比为4:9,则两三角形面积之比为 .15. 如图,一次函数y=kx+b的图象与反比例函数 的图象交于A(﹣2,1)、B(1,﹣2)两点.一次函数的值大于反比例函数的值时x的取值范围是 .
14. 两个相似三角形对应边上的中线之比为4:9,则两三角形面积之比为 .15. 如图,一次函数y=kx+b的图象与反比例函数 的图象交于A(﹣2,1)、B(1,﹣2)两点.一次函数的值大于反比例函数的值时x的取值范围是 . 16. 如图,在平面直角坐标系中,点A是函数 (x<0)图象上的点,过点A作y轴的垂线交y轴于点B , 点C在x轴上,若△ABC的面积为1,则k的值为 .
16. 如图,在平面直角坐标系中,点A是函数 (x<0)图象上的点,过点A作y轴的垂线交y轴于点B , 点C在x轴上,若△ABC的面积为1,则k的值为 . 17. 如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为 .
17. 如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为 .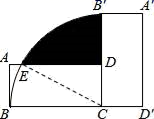 18. 如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A⇒B⇒A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当t为s时,△BEF是直角三角形.
18. 如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A⇒B⇒A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当t为s时,△BEF是直角三角形.
三、解答题
-
19. 在“植树节”期间,小王、小李两人想通过摸球的方式来决定谁去参加学校植树活动,规则如下:在两个盒子内分别装入标有数字1,2,3,4的四个和标有数字1,2,3的三个完全相同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于5,那么小王去,否则就是小李去.(1)、用树状图或列表法求出小王去的概率;(2)、小李说:“这种规则不公平”,你认同他的说法吗?请说明理由.20. 如图在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
 (1)、求证:△ADE∽△ABC;(2)、如AF=3,AG=5,求△ADE与△ABC的周长之比.21. 一次函数y=kx+b的图象与反比例函数 的图象相交于A(﹣1,m),B(n , -1)两点.
(1)、求证:△ADE∽△ABC;(2)、如AF=3,AG=5,求△ADE与△ABC的周长之比.21. 一次函数y=kx+b的图象与反比例函数 的图象相交于A(﹣1,m),B(n , -1)两点. (1)、求出这个一次函数的表达式;(2)、求△OAB的面积.22. 已知AB是⊙O的直径,弦CD与AB相交于点E , 连接AD , BC , 已知AE=AD , ∠BAD=34°.
(1)、求出这个一次函数的表达式;(2)、求△OAB的面积.22. 已知AB是⊙O的直径,弦CD与AB相交于点E , 连接AD , BC , 已知AE=AD , ∠BAD=34°. (1)、如图①,连接CO , 求∠ADC和∠OCD的大小;(2)、如图②,过点D作⊙O的切线与CB的延长线交于点F , 连接BD , 求∠BDF的大小.23.
(1)、如图①,连接CO , 求∠ADC和∠OCD的大小;(2)、如图②,过点D作⊙O的切线与CB的延长线交于点F , 连接BD , 求∠BDF的大小.23.如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
 (1)、求证:DE⊥AG(2)、
(1)、求证:DE⊥AG(2)、正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
 24. 在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A、B , C , 已知A(﹣1,0),C(0,3).
24. 在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A、B , C , 已知A(﹣1,0),C(0,3). (1)、求抛物线的解析式;(2)、如图1,P为线段BC上一动点,过点P作y轴的平行线,交抛物线于点D , 是否存在这样的P点,使线段PD的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)、如图2,抛物线的顶点为E , EF⊥x轴于点F , N是直线EF上一动点,M(m , 0)是x轴一个动点,请直接写出CN+MN+ MB的最小值以及此时点M、N的坐标,直接写出结果不必说明理由.
(1)、求抛物线的解析式;(2)、如图1,P为线段BC上一动点,过点P作y轴的平行线,交抛物线于点D , 是否存在这样的P点,使线段PD的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)、如图2,抛物线的顶点为E , EF⊥x轴于点F , N是直线EF上一动点,M(m , 0)是x轴一个动点,请直接写出CN+MN+ MB的最小值以及此时点M、N的坐标,直接写出结果不必说明理由.