天津市滨海新区2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是中心对称图形的是( )

A、 B、 C、 D、

查看试题解析
2. 抛物线 $y = - 2 {(x - 1)}^{2} + 3$ 的顶点坐标是（）

A、 $(1, 3)$ B、 $(- 1, 3)$ C、 $(1, - 3)$ D、 $(- 1, - 3)$

查看试题解析
3. 某个事件发生的概率是 $\frac{1}{2}$ ，这意味着 $($ 　　 $)$

A、在一次试验中没有发生，下次肯定发生 B、在一次事件中已经发生，下次肯定不发生 C、每次试验中事件发生的可能性是 $50 %$ D、在两次重复试验中该事件必有一次发生

查看试题解析
4. 已知 $Δ A B C \sim Δ D E F$ 且对应中线之比为 $9 ： 16$ ，则 $Δ A B C$ 与 $Δ D E F$ 的周长之比为 $($ 　　 $)$

A、 $4 ： 3$ B、 $3 ： 4$ C、 $16 ： 9$ D、 $9 ： 16$

查看试题解析
5. 如图，在 $6 \times 6$ 的正方形网格中，连结两格点A，B，点C、D是线段 $A B$ 与网格线的交点，则 $B C ： C D ： D A$ 为 $($ 　　 $)$

A、 $3 ： 4 ： 5$ B、 $1 ： 3 ： 2$ C、 $1 ： 4 ： 2$ D、 $3 ： 6 ： 5$

查看试题解析
6. 如图， $∠ A O B = 90 °$ ， $∠ B = 30 °$ ，将 $Δ A O B$ 绕点O顺时针旋转角度得到△ $A^{'} O B^{'}$ ，旋转角 $α$ 为．若点 $A^{'}$ 落在AB上，则旋转角 $α$ 的大小是（）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $90 °$

查看试题解析
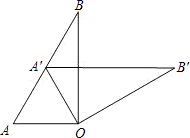7. 在半径为12的 $⊙ O$ 中， $150 °$ 的圆心角所对的弧长等于 $($ 　　 $)$

A、 $10 π$ B、 $12 π$ C、 $24 π$ D、 $5 π$

查看试题解析
8. 若抛物线 $y = {(x + 1)}^{2}$ 先向下平移2个单位长度，再向左平移1个单位长度，则所得到的新抛物线的解析式是 $($ 　　 $)$

A、 $y = {(x + 2)}^{2} + 2$ B、 $y = x^{2} - 2$ C、 $y = x^{2} + 2$ D、 $y = {(x + 2)}^{2} - 2$

查看试题解析
9. 若点 $(- 1 ， y_{1})$ ， $(2 ， y_{2})$ ， $(3 ， y_{3})$ 在反比例函数 $y = - \frac{5}{x}$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是 $($ 　　 $)$

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{2} > y_{3} > y_{1}$ C、 $y_{3} > y_{1} > y_{2}$ D、 $y_{1} > y_{3} > y_{2}$

查看试题解析
10. 如图⊙O的直径 $A B$ 垂直于弦 $C D$ ，垂足是 $E$ ， $∠ A = 22.5 °$ ， $O C = 4$ ， $C D$ 的长为（）

A、 B、4 C、 D、8

查看试题解析
11. 如图，边长为1的正方形 $A B C D$ 绕点A逆时针旋转得到正方形 $A B_{1} C_{1} D_{1}$ ，使边 $A B_{1}$ 恰好落在对角线AC上，边 $B_{1} C_{1}$ 与 $C D$ 交于点O，则四边形 $A B_{1} O D$ 的面积是 $($ 　　 $)$

A、 $\frac{3}{4}$ B、 $\frac{7}{16}$ C、 $\sqrt{2} - 1$ D、 $\frac{\sqrt{2} - 1}{2}$

查看试题解析
12. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示， $c < - 1$ ，其对称轴为直线 $x = - 1$ ，与 $x$ 轴的交点为 $(x_{1}$ ， $0)$ 、 $(x_{2}$ ， $0)$ ，其中 $0 < x_{1} < 1$ ，有下列结论：① $a b c > 0$ ；② $- 3 < x_{2} < - 2$ ；③ $4 a - 2 b + c < - 1$ ；④ $a - b > a m^{2} + b m (m \neq - 1)$ ；其中，正确的结论个数是 $($ 　　 $)$

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 将二次函数 $y = x^{2} - 4 x + 5$ 化成 $y = a {(x - h)}^{2} + k$ 的形式为.

查看试题解析
14. 已知反比例函数 $y = \frac{k}{x} (k$ 为常数， $k \neq 0)$ 的图象经过点 $P (2, 2)$ ，当 $1 < x < 2$ 时，则y的取值范围是．

查看试题解析
15. 如图，□ABCD中，点E是AD边的中点，BE交对角线AC于点F，若AF=2，则对角线AC长为.

查看试题解析
16. 如图， $Δ P Q R$ 是 $⊙ O$ 的内接正三角形，四边形 $A B C D$ 是 $⊙ O$ 的内接正方形， $B C / / Q R$ ，则 $∠ B O Q =$ ．

查看试题解析
17. 如图，将Rt△ABC绕点C按顺时针方向旋转90°到△A′B′C的位置，已知斜边AB=10cm，BC=6cm，设A′B′的中点是M，连结AM，则AM=cm．

查看试题解析
18. 如图，在每个小正方形边长为1的网格中， $△ A B C$ 的顶点A，B，C均在格点上，D为 $A C$ 边上的一点.

（Ⅰ）线段 $A C$ 的值为；

（Ⅱ）在如图所示的网格中， $A M$ 是 $△ A B C$ 的角平分线，在 $A M$ 上求一点P，使 $C P + D P$ 的值最小，请用无刻度的直尺，画出 $A M$ 和点P，并简要说明 $A M$ 和点P的位置是如何找到的（不要求证明）.

查看试题解析

三、解答题

19. 已知图中的曲线是反比例函数 $y = \frac{m - 5}{x} (m$ 为常数）图象的一支．

(1)、这个反比例函数图象的另一支在第几象限？常数m的取值范围是什么？

(2)、若该函数的图象与正比例函数 $y = 2 x$ 的图象在第一象限内的交点为A，过A点作x轴的垂线，垂足为B，当 $Δ O A B$ 的面积为4时，求点A的坐标及反比例函数的关系式．

查看试题解析
20. 一个不透明的布袋里装有4个大小、质地都相同的乒乓球，球面上分别标有数字1，2，3，4，小明先从布袋中随机摸出一个乒乓球，不放回去，再从剩下的3个球中随机摸出第二个乒乓球．

(1)、求小明第一次摸出的乒乓球所标数字是偶数的概率；

(2)、请用树状图或列表的方法求两次摸出的乒乓球球面上数字的积为偶数的概率．

查看试题解析
21. 如图，四边形 $A B C D$ 中 $A B / / C D$ ，点F在 $B C$ 上，连 $D F$ 与 $A B$ 的延长线交于点G．

(1)、求证： $Δ C D F ∽ Δ B G F$ ；

(2)、当点F是 $B C$ 的中点时，过F作 $E F / / C D$ 交 $A D$ 于点E，若 $A B = 6$ ， $E F = 4$ ，求 $B G$ 的长．

查看试题解析
22. 如图，在 $Δ A B C$ 中， $∠ A B C = 90 °$ ， $A B = 8$ ， $B C = 6$ ．以 $B C$ 为直径的 $⊙ O$ 交 $A C$ 于D，E是 $A B$ 的中点，连接 $E D$ 并延长交 $B C$ 的延长线于点F．

(1)、求证： $D E$ 是 $⊙ O$ 的切线；

(2)、求 $D B$ 的长．

查看试题解析
23. 商城某种商品平均每天可销售20件，每件盈利30元，为庆元旦，决定进行促销活动，经调查发现，每件商品每降价1元，商场平均每天可多售出2件．设该商品每件降价x元，请解答下列问题

(1)、用含x的代数式表示：
①降价后每售一件盈利元；

②降价后平均每天售出件；

(2)、在此次促销活动中，商城若要获得最大盈利，每件商品应降价多少元？获得最大盈利多少元？

查看试题解析
24. 已知 $Δ A B C$ 中， $A B = A C$ ，D、E是 $B C$ 边上的点，将 $Δ A B D$ 绕点A旋转，得到 $Δ A C D^{'}$ ，连结 $D^{'} E$ ．

(1)、如图1，当 $∠ B A C = 120 °$ ， $∠ D A E = 60 °$ 时，求 $∠ D^{'} A E$ 的度数；

(2)、如图2，当 $D E = D^{'} E$ 时，求证： $∠ D A E = \frac{1}{2}$ $∠ B A C$ ．

(3)、如图3，在（2）的结论下，当 $∠ B A C = 90 °$ ， $B D$ 与 $D E$ 满足怎样的数量关系时，△ $D^{'} E C$ 是等腰直角三角形？（直接写出结论，不必说明理由）

查看试题解析
25. 如图，在平面直角坐标系中，抛物线y=ax²+bx+3与x轴交于A（﹣4，0）、B（﹣1，0）两点，与y轴交于点C，点D是第三象限的抛物线上一动点．

(1)、求抛物线的解析式；

(2)、设点D的横坐标为m，△ACD的面积为量求出S与m的函数关系式，并确定m为何值时S有最大值，最大值是多少？

(3)、若点P是抛物线对称轴上一点，是否存在点P使得∠APC=90°？若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析