河北省唐山市遵化市2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中，是一元二次方程的是(　　)

A、 $a x^{2} + b x + c$ B、 $\frac{x^{2} + 1}{2} - \frac{x - 1}{2} = 1$ C、 $\sqrt{x - 1} + x^{2} = 1$ D、 $x^{3} + x + 1 = 0$

查看试题解析
2. 已知 $y = 2 x^{2 m}$ 是关于x的反比例函数，则(　　)

A、 $m = \frac{1}{2}$ B、 $m = - \frac{1}{2}$ C、 $m \neq 0$ D、 $m$ 为一切实数

查看试题解析
3. 已知A样本的数据如下：72，73，76，76，77，78，78，78，B样本的数据恰好是A样本数据每个的2倍，则A，B两个样本的方差关系是（）

A、B是A的 $\sqrt{2}$ 倍 B、B是A的2倍 C、B是A的4倍 D、一样大

查看试题解析
4. 如果一个多边形的内角和是外角和的3倍，则这个多边形的边数是（）

A、8 B、9 C、10 D、11

查看试题解析
5. 如图，已知矩形ABCD和矩形EFGO在平面直角坐标系中，点B ， F的坐标分别为(－4，4)，(2，1)．若矩形ABCD和矩形EFGO是位似图形，点P(点P在GC上)是位似中心，则点P的坐标为(　　)

A、(0，3) B、(0，2.5) C、(0，2) D、(0，1.5)

查看试题解析
6. 在平面直角坐标系xOy中，以点(－3，4)为圆心，4为半径的圆（）

A、与x轴相交，与y轴相切 B、与x轴相离，与y轴相交 C、与x轴相切，与y轴相交 D、与x轴相切，与y轴相离

查看试题解析
7. 已知将二次函数y=x²+bx+c的图象向右平移2个单位，再向下平移3个单位，所得图象的解析式为y=x²-4x-5，则b，c的值为（）

A、b=0，c=6 B、b=0．c= -5 C、b=0．c= -6 D、b=0,c=5

查看试题解析
8. 如图，在Rt△ABC中，∠ACB＝90°，⊙O是△ABC的内切圆，三个切点分别为D、E、F，若BF＝2，AF＝3，则△ABC的面积是（）

A、6 B、7 C、 $\frac{\sqrt{3}}{2}$ D、12

查看试题解析
9. 一元二次方程 $a x^{2} + b x + c = 0$ 中至少有一个根是零的条件是(　　)

A、 $c = 0$ 且 $b \neq 0$ B、 $b = 0$ C、 $c = 0$ 且 $b = 0$ D、 $c = 0$

查看试题解析
10. 函数y＝ $\frac{k}{x}$ 与y＝kx＋k(k为常数且k≠0)在同一平面直角坐标系中的图象可能是(　　)

A、 B、 C、 D、

查看试题解析
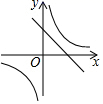11. 已知二次函数的图象与x轴的一个交点为(-1，0)，对称轴是直线 $x = 1$ ，则图象与x轴的另一个交点是(　　)

A、(2，0) B、(-3，0) C、(-2，0) D、(3，0)

查看试题解析
12. 若角 $α ， β$ 都是锐角，以下结论：①若 $α < β$ ，则 $\sin α < \sin β$ ；②若 $α < β$ ，则 $\cos α < \cos β$ ；③若 $α < β$ ，则 $\tan α < \tan β$ ；④若 $α + β = 90^{\circ}$ ，则 $\sin α = \cos β$ .其中正确的是(　　)

A、①② B、①②③ C、①③④ D、①②③④

查看试题解析
13. 若二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象的顶点在第一象限，且经过点(0，1)和(-1，0)，则 $S = a + b + c$ 的值的变化范围是（）

A、 $0 < S < 2$ B、 $0 < S < 1$ C、 $1 < S < 2$ D、 $- 1 < S < 1$

查看试题解析
14.
如图，在锐角△ABC中，∠A=60°，∠ACB=45°，以BC为弦作⊙O，交AC于点D，OD与BC交于点E，若AB与⊙O相切，则下列结论：
①∠BOD=90°；②DO∥AB；③CD=AD；④△BDE∽△BCD；⑤ $\frac{B E}{D E}$ = $\sqrt{2}$
正确的有（　　）

A、①② B、①④⑤ C、①②④⑤ D、①②③④⑤

查看试题解析
15. 已知二次函数 $y = x^{2} - x + a (a > 0)$ ，当自变量 $x$ 取 $m$ 时，其相应的函数值小于0，则下列结论正确的是（）

A、 $x$ 取 $m - 1$ 时的函数值小于0 B、 $x$ 取 $m - 1$ 时的函数值大于0 C、 $x$ 取 $m - 1$ 时的函数值等于0 D、 $x$ 取 $m - 1$ 时函数值与0的大小关系不确定

查看试题解析
16. 四边形 $A B C D$ 内接于⊙ $O$ ，点I是 $Δ A B C$ 的内心， $∠ A I C = 124^{\circ}$ ，点E在 $A D$ 的延长线上，则 $∠ C D E$ 的度数为(　　)

A、56° B、62° C、68° D、48°

查看试题解析

二、填空题

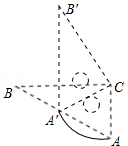
17. 中国“一带一路”给沿线国家和地区带来很大的经济效益，沿线某地区居民2016年人均年收入20000元，到2018年人均年收入达到39200元.则该地区居民年人均收入平均增长率为.(用百分数表示)

查看试题解析
18. 如图，△ABC和△A′B′C是两个完全重合的直角三角板，∠B=30°，斜边长为10cm．三角板A′B′C绕直角顶点C顺时针旋转，当点A′落在AB边上时，CA′旋转所构成的扇形的弧长为cm．

查看试题解析
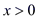19. 如图，点M是反比例函数 $y = \frac{2}{x}$ （）图象上任意一点，AB⊥y轴于B ，点C是x轴上的动点，则△ABC的面积为．

查看试题解析

三、解答题

20.

(1)、计算： $| \sqrt{3} - 2 | + {(\frac{1}{2020 - x})}^{0} + 3 \tan 30^{\circ} + \sqrt[3]{8}$ ．

(2)、解方程： ${(x - \sqrt{2})}^{2} = 5 \times (\sqrt{2} - x)$ ．

查看试题解析
21. 在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=xm．

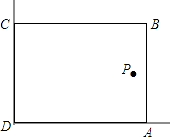(1)、若花园的面积为192m² ，求x的值；

(2)、若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），求花园面积S的最大值．

查看试题解析
22. 如图是由6个形状、大小完全相同的小矩形组成的，小矩形的顶点称为格点．已知小矩形较短边长为1， $Δ A B C$ 的顶点都在格点上．

(1)、用无刻度的直尺作图：找出格点D，连接 $C D$ ，使 $∠ A C D = 90^{\circ}$ ；

(2)、在（1）的条件下，连接 $A D$ ，求 $\tan ∠ B A D$ 的值．

查看试题解析
23. 我市某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在自然光照且温度为 $18 ° C$ 的条件下生长最快的新品种．下图是某天恒温系统从开启到关闭及关闭后，大棚内温度y（℃）随时间x（小时）变化的函数图象，其中 $B C$ 段是双曲线 $y = \frac{k}{x}$ 的一部分．请根据图中信息解答下列问题：

(1)、恒温系统在这天保持大棚内温度 $18 ° C$ 的时间有小时；

(2)、当 $x = 15$ 时，大棚内的温度约为多少度？

查看试题解析
24. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90^{\circ}$ ， $C D ⊥ A B$ ，垂足为D，E为 $B C$ 上一点，连接 $A E$ ，作 $E F ⊥ A E$ 交 $A B$ 于 $F$ ．

(1)、求证： $Δ A G C \sim Δ E F B$ ．

(2)、除（1）中相似三角形，图中还有其他相似三角形吗？如果有，请把它们都写出来．(证明不做要求)

查看试题解析
25. 如图，BD为△ABC外接圆⊙O的直径，且∠BAE=∠C．

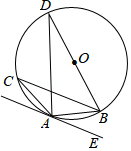(1)、求证：AE与⊙O相切于点A；

(2)、若AE∥BC，BC=2 $\sqrt{7}$ ，AC=2 $\sqrt{2}$ ，求AD的长．

查看试题解析
26. 通过实验研究，专家们发现：初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的．讲课开始时，学生的兴趣激增，中间有一段时间的兴趣保持平稳状态，随后开始分散．学生注意力指标数y随时间x( $\min$ )变化的函数图象如图所示(y越大表示注意力越集中)．当 $0 \leq x \leq 10$ 时，图象是抛物线的一部分，当 $10 \leq x \leq 20$ 和 $20 \leq x \leq 40$ 时，图象是线段．

(1)、当 $0 \leq x \leq 10$ 时，求注意力指标数y与时间x的函数关系式．

(2)、一道数学综合题，需要讲解24 $\min$ ，问老师能否安排，使学生听这道题时，注意力的指标数都不低于36．

查看试题解析