河北省唐山市滦南县2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. cos30°的值是（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
2. 用配方法解方程 $x^{2} - 6 x - 4 = 0$ ，下列配方正确的是（）

A、 ${(x - 3)}^{2} = 13$ B、 ${(x + 3)}^{2} = 13$ C、 ${(x - 6)}^{2} = 4$ D、 ${(x - 3)}^{2} = 5$

查看试题解析
3. 如图，把一个量角器放在 $∠ B A C$ 的上面，点B恰好在量角器上 $40 °$ 的位置，则 $∠ B A C$ 的度数是（）

A、 $40 °$ B、 $80 °$ C、 $20 °$ D、 $10 °$

查看试题解析
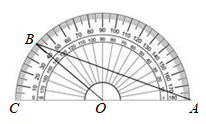4. 小明记录了临沂市五月份某周每天的日最高气温(单位： $° C$ )，列成如表：

天数(天)

1

2

1

3

最高气温( $° C$ )

22

26

28

29

则这周最高气温的平均值是（）

A、 $26.25 ° C$ B、 $27 ° C$ C、 $28 ° C$ D、 $29 ° C$

查看试题解析
5. 如果3x＝4y，那么下列各式中正确的是（　　）

A、 $\frac{x}{y} = \frac{3}{4}$ B、 $\frac{x}{x - y} = 4$ C、 $\frac{x + y}{y} = \frac{7}{4}$ D、 $\frac{x}{x + y} = \frac{3}{7}$

查看试题解析
6. 如图所示，点A是反比例函数y＝ $\frac{k}{x}$ 的图象上的一点，过点A作AB⊥x轴，垂足为B，点C为y轴上的一点，连接AC、BC．若△ABC的面积为5，则k的值为（）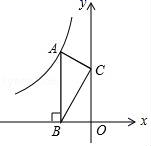

A、5 B、﹣5 C、10 D、﹣10

查看试题解析
7. 若a、b是关于x的一元二次方程x²﹣6x+n+1=0的两根，且等腰三角形三边长分别为a、b、4，则n的值为（）

A、8 B、7 C、8或7 D、9或8

查看试题解析
8. 如图所示，在长为8cm，宽为6cm的矩形中，截去一个矩形（图中阴影部分），如果剩下的矩形与原矩形相似，那么剩下矩形的面积是（）

A、28cm² B、27cm² C、21cm² D、20cm²

查看试题解析
9. 如图，⊙O的直径CD＝12cm，AB是⊙O的弦，AB⊥CD，垂足为E，OE：OC＝1：3，则AB的长为（　　）

A、2 $\sqrt{2}$ cm B、4 $\sqrt{2}$ cm C、6 $\sqrt{2}$ cm D、8 $\sqrt{2}$ cm

查看试题解析
10. 二次函数 $y = a x^{2} + b x$ 的图象如图所示，若一元二次方程 $a x^{2} + b x = - m$ 有实数根，则m的最大（）

A、3 B、 $- 3$ C、 $- 6$ D、9

查看试题解析
11. 在直角坐标平面内，已知点M(4，3)，以M为圆心，r为半径的圆与x轴相交，与y轴相离，那么r的取值范围为（）

A、 $0 < r < 5$ B、 $3 < r < 5$ C、 $4 < r < 5$ D、 $3 < r < 4$

查看试题解析
12.
如图，一艘轮船以40海里/时的速度在海面上航行，当它行驶到A处时，发现它的北偏东30°方向有一灯塔B．轮船继续向北航行2小时后到达C处，发现灯塔B在它的北偏东60°方向．若轮船继续向北航行，那么当再过多长时间时轮船离灯塔最近？（）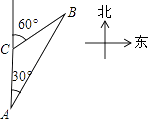

A、1小时 B、 $\sqrt{3}$ 小时 C、2小时 D、 $2 \sqrt{3}$ 小时

查看试题解析
13. 如图，圆锥的侧面展开图是半径为4，圆心角为90°的扇形，则该圆锥的底面周长为（）

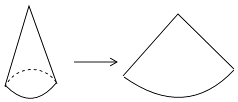A、π B、2π C、8π D、16

查看试题解析
14. 在平面直角坐标系中有两点 $A (- 2 ， 4) ， B (2 ， 4)$ ，若二次函数 $y = a x^{2} - 2 a x - 3 a (a \neq 0)$ 的图像与线段AB只有一个交点，则（　　）

A、a的值可以是 $- \frac{4}{3}$ B、a的值可以是 $\frac{3}{5}$ C、a的值不可能是-1.2 D、a的值不可能是-1

查看试题解析
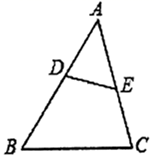15. 如图，点D、E分别在 $Δ A B C$ 的 $A B$ 、 $A C$ 边上，增加下列哪些条件：① $∠ A E D = ∠ B$ ；② $\frac{A E}{A B} = \frac{D E}{B C}$ ；③ $\frac{A D}{A C} = \frac{A E}{A B}$ ，使 $Δ A D E$ 与 $Δ A C B$ 一定相似（）

A、①③ B、②③ C、①② D、①②③

查看试题解析
16. 为了响应“绿水青山就是金山银山”的号召，建设生态文明，某工厂自2019年1月开始限产并进行治污改造，其月利润y(万元)与月份x之间的变化如图所示，治污完成前是反比例函数图象的一部分，治污完成后是一次函数图象的部分，下列选项错误的是（）

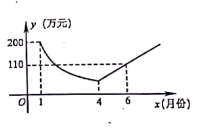A、4月份的利润为 $50$ 万元 B、污改造完成后每月利润比前一个月增加 $30$ 万元 C、治污改造完成前后共有 $4$ 个月的利润低于 $100$ 万元 D、9月份该厂利润达到 $200$ 万元

查看试题解析

二、填空题

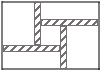
17. 工人师傅童威准备在一块长为60，宽为48的长方形花圃内修建四条宽度相等，且与各边垂直的小路.四条小路围成的中间部分恰好是一个正方形，且边长是小路宽度的8倍.若四条小路所占面积为160.设小路的宽度为x，依题意列方程，化为一般形式为

查看试题解析
18. 在平面直角坐标系中有 $A$ ， $B$ ， $C$ 三点， $A (1, 3)$ ， $B (3, 3)$ ， $C (5, 1)$ ．现在要画一个圆同时经过这三点，则圆心坐标为．

查看试题解析
19. 为测量学校旗杆的高度，小明的测量方法如下：如图，将直角三角形硬纸板DEF的斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上．测得DE＝0.5米，EF＝0.25米，目测点D到地面的距离DG＝1.5米，到旗杆的水平距离DC＝20米．按此方法，请计算旗杆的高度为米．

查看试题解析
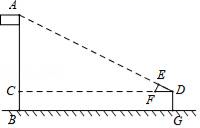20. 如图，平面坐标内，矩形 $A O C D$ 的顶点 $A (0 ， 2)$ 、 $C (4 ， 0)$ 、 $D (4 ， 2)$ ，抛物线 $y = x^{2} - 1$ 经过点 $Q (a ， 4)$ ， $P (b ， 4)$ ， $⊙ P$ 的半径为1，当圆心P在抛物线上从点P运动到点Q，则在整个运动过程中， $⊙ P$ 与矩形 $A O C D$ 只有一个公共点的情况共出现次．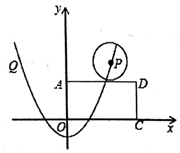

查看试题解析

三、解答题

21. 如图是某货站传送货物的平面示意图为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角使其由 $45 °$ 改为 $30 °$ ，已知原传送带 $A B$ 长为4米．

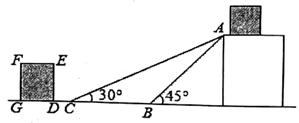(1)、求新传送带 $A C$ 的长度；（结果保留根号）

(2)、如果需要在货物着地点C的左侧留出2米的通道，试判断距离 $B$ 点5米的货物 $D E F G$ 是否需要挪走，并说明理由（结果精确到0.1米参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ， $\sqrt{6} \approx 2.45$ ）

查看试题解析

22. 某中学形展“唱红歌”比赛活动，九年级（1）、（2）班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩如图所示．

(1)、根据图示填写下表：

班级	平均数（分）	中位数（分）	众数（分）
九（1）		85
九（2）	85		100

(2)、结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好；

(3)、计算两班复赛成绩的方差．

查看试题解析

23. 如图， $A B$ 为 $⊙ O$ 的直径，C为 $⊙ O$ 上一点， $A D$ 和过C点的直线互相垂直，垂足为D，且 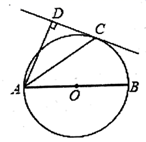$A C$ 平分 $∠ D A B$ ．

(1)、求证： $D C$ 为 $⊙ O$ 的切线；

(2)、若 $∠ D A B = 60 °$ ， $⊙ O$ 的半径为3，求线段 $A C$ 的长．

查看试题解析
24. 直线 $y = m x$ （m为常数）与双曲线 $y = \frac{k}{x}$ （ $k$ 为常数）相交于A、B两点．

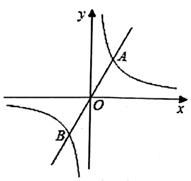(1)、若点A的横坐标为3，点B的纵坐标为-4．直接写出： $k =$ ， $m =$ ， $m x > \frac{k}{x}$ 的解集为．

(2)、若双曲线 $y = \frac{k}{x}$ （k为常数）的图象上有点 $C (x_{1} ， y_{1})$ ， $D (x_{2} ， y_{2})$ ，当 $x_{1} < x_{2}$ 时，比较 $y_{1}$ 与 $y_{2}$ 的大小．

查看试题解析
25. 如图，在正方形 $A B C D$ 中，点M是边 $B C$ 上的一点（不与B、C重合），点N在 $C D$ 的延长线上，且满足 $∠ M A N = 90 °$ ，连接 $M N$ 、 $A C$ ， $M N$ 与边 $A D$ 交于点E．

(1)、求证： $A M = A N$ ；

(2)、如果 $∠ C A D = 2 ∠ N A D$ ，求证： $A N^{2} = A E \cdot A C$ ．

查看试题解析
26. 如图，已知抛物线 $y = a^{2} + b x + 3 (a \neq 0)$ 经过点 $A (1 ， 0)$ 和点 $B (3 ， 0)$ ，与y轴交于点C.

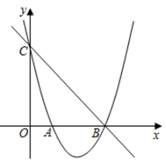(1)、求此抛物线的解析式；

(2)、若点P是直线 $B C$ 下方的抛物线上一动点（不点B，C重合），过点P作y轴的平行线交直线 $B C$ 于点D，设点P的横坐标为m.
①用含m的代数式表示线段 $P D$ 的长；

②连接 $P B$ ， $P C$ ，求 $Δ P B C$ 的面积最大时点P的坐标；

(3)、设抛物线的对称轴与 $B C$ 交于点E，点M是抛物线的对称轴上一点，N为y轴上一点，是否存在这样的点M和点N，使得以点C、E、M、N为顶点的四边形是菱形？如果存在，请直接写出点M的坐标；如果不存在，请说明理由.

查看试题解析

天数(天)	1	2	1	3
最高气温( $° C$ )	22	26	28	29