河北省唐山市路南区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-05 类型:期末考试
一、单选题
-
1. 下列几何体的三视图相同的是( )A、
 圆柱
B、
圆柱
B、 球
C、
球
C、 圆锥
D、
圆锥
D、 长方体
2. 点A(-2,1)关于原点对称的点A'的坐标是( )A、(2,1) B、(-2,-1) C、(-1,2) D、(2,-1)3. 下列光线所形成的投影不是中心投影的是( )A、太阳光线 B、台灯的光线 C、手电筒的光线 D、路灯的光线4. 下列成语描述的事件为随机事件的是( )A、水涨船高 B、守株待兔 C、水中捞月 D、缘木求鱼5. 下列函数中, y是x的反比例函数( )A、 B、 C、 D、6. 在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率,其实验次数分别为10次、50次、100次,200次,其中实验相对科学的是( )A、甲组 B、乙组 C、丙组 D、丁组7. 已知反比例函数 ,下列结论中错误的是. ( )A、图象必经过点(3,-2) B、图象位于第二、四象限 C、若 ,则 D、在每一个象限内, y随x值的增大而增大8. 若点 在抛物线 上,则 的值( )A、2021 B、2020 C、2019 D、20189. 下列说法中,正确的个数( )
长方体
2. 点A(-2,1)关于原点对称的点A'的坐标是( )A、(2,1) B、(-2,-1) C、(-1,2) D、(2,-1)3. 下列光线所形成的投影不是中心投影的是( )A、太阳光线 B、台灯的光线 C、手电筒的光线 D、路灯的光线4. 下列成语描述的事件为随机事件的是( )A、水涨船高 B、守株待兔 C、水中捞月 D、缘木求鱼5. 下列函数中, y是x的反比例函数( )A、 B、 C、 D、6. 在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率,其实验次数分别为10次、50次、100次,200次,其中实验相对科学的是( )A、甲组 B、乙组 C、丙组 D、丁组7. 已知反比例函数 ,下列结论中错误的是. ( )A、图象必经过点(3,-2) B、图象位于第二、四象限 C、若 ,则 D、在每一个象限内, y随x值的增大而增大8. 若点 在抛物线 上,则 的值( )A、2021 B、2020 C、2019 D、20189. 下列说法中,正确的个数( )①位似图形都相似:
②两个等边三角形一定是位似图形;
③两个相似多边形的面积比为5:9.则周长的比为5:9;
④两个大小不相等的圆一定是位似图形.
A、1个 B、2个 C、3个 D、4个10.河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1: ,则AB的长为( )
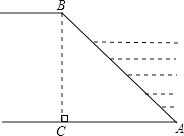 A、12米 B、4 米 C、5 米 D、6 米11.
A、12米 B、4 米 C、5 米 D、6 米11.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )
 A、2π B、4π C、5π D、6π12. 若二次函数 的图象与 x轴仅有一个公共点,则常数k的为( )A、1 B、±1 C、-1 D、13. 到 的三顶点距离相等的点是 的是( )A、三条中线的交点 B、三条角平分线的交点 C、三条高线的交点 D、三条边的垂直平分线的交点14. 如图,如果∠BAD=∠CAE,那么添加下列一个条件后,仍不能确定△ABC∽△ADE的是( )
A、2π B、4π C、5π D、6π12. 若二次函数 的图象与 x轴仅有一个公共点,则常数k的为( )A、1 B、±1 C、-1 D、13. 到 的三顶点距离相等的点是 的是( )A、三条中线的交点 B、三条角平分线的交点 C、三条高线的交点 D、三条边的垂直平分线的交点14. 如图,如果∠BAD=∠CAE,那么添加下列一个条件后,仍不能确定△ABC∽△ADE的是( )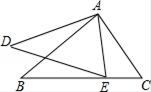 A、∠B=∠D B、∠C=∠AED C、 = D、 =15. 生产季节性产品的企业,当它的产品无利润时就会及时停产.现有一生产季节性产品的企业,其一年中获得的利润y和月份n之间的函数关系式为 ,则该企业一年中应停产的月份是( )A、1月、2月、3月 B、2月、3月、4月 C、1月、2月、12月 D、1月、11月、12月
A、∠B=∠D B、∠C=∠AED C、 = D、 =15. 生产季节性产品的企业,当它的产品无利润时就会及时停产.现有一生产季节性产品的企业,其一年中获得的利润y和月份n之间的函数关系式为 ,则该企业一年中应停产的月份是( )A、1月、2月、3月 B、2月、3月、4月 C、1月、2月、12月 D、1月、11月、12月二、填空题
-
16. 二次函数 图象的开口向 .17. 两地的实际距离是 ,在地图上众得这两地的距离为 ,则这幅地图的比例尺是 .18. 如图,用长 的铝合金条制成使窗户的透光面积最大的矩形窗框,那么这个窗户的最大透光面积是 .(中间横框所占的面积忽略不计)

三、解答题
-
19.(1)、解方程: ;(2)、计算: .20. 如图,是由两个长方体组合而成的一个立体图形的主视图和左视图,根据图中所标尺寸(单位: mm).
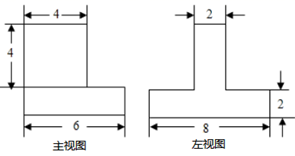 (1)、直接写出上下两个长方休的长、宽、商分别是多少:(2)、求这个立体图形的体积.21. 如图, 相交于点P,连结 .
(1)、直接写出上下两个长方休的长、宽、商分别是多少:(2)、求这个立体图形的体积.21. 如图, 相交于点P,连结 .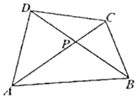 (1)、求证: ;(2)、直接回答 与 是不是位似图形?(3)、若 ,求 的长.22. 如图,有四张质地完全相同的卡片,正面分别写有四个角度,现将这四张卡片洗匀后,背面朝上.
(1)、求证: ;(2)、直接回答 与 是不是位似图形?(3)、若 ,求 的长.22. 如图,有四张质地完全相同的卡片,正面分别写有四个角度,现将这四张卡片洗匀后,背面朝上. (1)、若从中任意抽取--张,求抽到锐角卡片的概宰;(2)、若从中任意抽取两张,求抽到的两张角度恰好互补的概率.23. 如图,在平面直角坐标系中,已知矩形 的顶点 ,过点 的双曲线 与矩形 的边 交于点E.
(1)、若从中任意抽取--张,求抽到锐角卡片的概宰;(2)、若从中任意抽取两张,求抽到的两张角度恰好互补的概率.23. 如图,在平面直角坐标系中,已知矩形 的顶点 ,过点 的双曲线 与矩形 的边 交于点E. (1)、求双曲线 的解析式以及点E的坐标;.(2)、若点P是抛物线 的顶点;
(1)、求双曲线 的解析式以及点E的坐标;.(2)、若点P是抛物线 的顶点;①当双曲线 过点P时,求顶点P的坐标;
②直接写出当抛物线 过点B时,该抛物线与矩形 公共点的个数以及此时t的值.
24. 如图,在南北方向的海岸线 上,有 两艘巡逻船,现均收到故障船C的求救信号.已知 两船相距 海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上, 上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.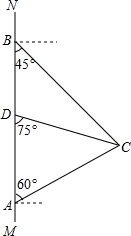 (1)、分别求出A与C,A与D间的距离 和 ; (本问如果有根号,结果请保留根号) (此提示可以帮助你解题:∵ ,∴ )(2)、已知距观测点D处100海里范围内有暗礁,若巡逻船A沿直线 去营救船C,去营救的途中有无触礁的危险?(参考数据: )25. 游乐园新建的一种新型水上滑道如图,其中线段 表示距离水面(x轴)高度为5m的平台(点P在y轴上).滑道 可以看作反比例函数图象的一部分,滑道 可以看作是二次函数图象的一部分,两滑道的连接点B为二次函数 的顶点,且点B到水面的距离 ,点B到y轴的距离是5m.当小明从上而下滑到点C时,与水面的距离 ,与点B的水平距离 .
(1)、分别求出A与C,A与D间的距离 和 ; (本问如果有根号,结果请保留根号) (此提示可以帮助你解题:∵ ,∴ )(2)、已知距观测点D处100海里范围内有暗礁,若巡逻船A沿直线 去营救船C,去营救的途中有无触礁的危险?(参考数据: )25. 游乐园新建的一种新型水上滑道如图,其中线段 表示距离水面(x轴)高度为5m的平台(点P在y轴上).滑道 可以看作反比例函数图象的一部分,滑道 可以看作是二次函数图象的一部分,两滑道的连接点B为二次函数 的顶点,且点B到水面的距离 ,点B到y轴的距离是5m.当小明从上而下滑到点C时,与水面的距离 ,与点B的水平距离 .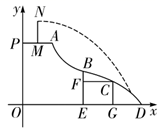 (1)、求反比例函数的关系式及其自变量的取值范围;(2)、求整条滑道 的水平距离;(3)、若小明站在平台上相距y轴1m的点M处,用水枪朝正前方向下“扫射”,水枪出水口N距离平台 ,喷出的水流成抛物线形,设这条抛物线的二次项系数为p,若水流最终落在滑道 上(包括B、D两点),直接写出p的取值范围.
(1)、求反比例函数的关系式及其自变量的取值范围;(2)、求整条滑道 的水平距离;(3)、若小明站在平台上相距y轴1m的点M处,用水枪朝正前方向下“扫射”,水枪出水口N距离平台 ,喷出的水流成抛物线形,设这条抛物线的二次项系数为p,若水流最终落在滑道 上(包括B、D两点),直接写出p的取值范围.