河北省秦皇岛市海港区2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下面的图形中，既是轴对称图形又是中心对称图形的是（）．

A、 B、 C、 D、

查看试题解析
2. 下列事件中，属于必然事件的是（）

A、明天我市下雨 B、抛一枚硬币，正面朝下 C、购买一张福利彩票中奖了 D、掷一枚骰子，向上一面的数字一定大于零

查看试题解析
3. 用配方法解方程 $x^{2} = 4 x + 1$ ，配方后得到的方程是（）

A、 ${(x - 2)}^{2} = 5$ B、 ${(x - 2)}^{2} = 4$ C、 ${(x - 2)}^{2} = 3$ D、 ${(x - 2)}^{2} = 14$

查看试题解析
4. 如图，以点O为位似中心，把△ABC放大为原图形的2倍得到△A'B'C'，以下说法中错误的是（）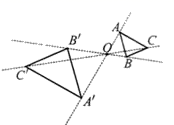

A、△ABC∽△A'B'C' B、点C、点O、点C'三点在同一直线上 C、AO：AA'=1∶2 D、AB∥A'B'

查看试题解析
5. 某射击运动员在训练中射击了10次，成绩如图所示：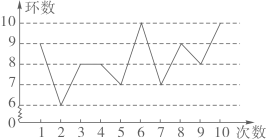

下列结论错误的是（）

A、众数是8 B、中位数是8 C、平均数是8.2 D、方差是1.2

查看试题解析
6. 对于二次函数 $y = 3 {(x - 2)}^{2} + 1$ 的图象，下列说法正确的是（）

A、开口向下 B、顶点坐标是 $(2, 1)$ C、对称轴是直线 $x = - 2$ D、与x轴有两个交点

查看试题解析
7. 国家实施”精准扶贫“政策以来，很多贫困人口走向了致富的道路．某地区2016年底有贫困人口9万人，通过社会各界的努力，2018年底贫困人口减少至1万人．设2016年底至2018年底该地区贫困人口的年平均下降率为 $x$ ，根据题意列方程得（）

A、 $9 (1 - 2 x) = 1$ B、 $9 {(1 - x)}^{2} = 1$ C、 $9 (1 + 2 x) = 1$ D、 $9 {(1 + x)}^{2} = 1$

查看试题解析
8. 已知反比例函数 $y = \frac{k}{x}$ 图象如图所示，下列说法正确的是（）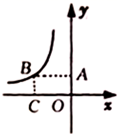

A、 $k > 0$ B、 $y$ 随 $x$ 的增大而减小 C、若矩形 $O A B C$ 面积为2，则 $k = 2$ D、若图象上两个点的坐标分别是 $M (- 2 ， y_{1})$ ， $N (- 1 ， y_{2})$ ，则 $y_{1} < y_{2}$

查看试题解析
9. 如图，从一张腰长为 $90 c m$ ，顶角为 $120^{°}$ 的等腰三角形铁皮 $O A B$ 中剪出一个最大的扇形 $O C D$ ，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的底面半径为（）

A、 $15 c m$ B、 $12 c m$ C、 $10 c m$ D、 $20 c m$

查看试题解析
10. 如图，嘉淇一家驾车从 $A$ 地出发，沿着北偏东 $60 °$ 的方向行驶，到达 $B$ 地后沿着南偏东 $50 °$ 的方向行驶来到 $C$ 地，且 $C$ 地恰好位于 $A$ 地正东方向上，则下列说法正确的是（）

A、 $B$ 地在 $C$ 地的北偏西 $40 °$ 方向上 B、 $A$ 地在 $B$ 地的南偏西 $30 °$ 方向上 C、 $\cos ∠ B A C = \frac{\sqrt{3}}{2}$ D、 $∠ A C B = 50 °$

查看试题解析
11. 对于一元二次方程 $x^{2} - 3 x + c = 0$ 来说，当 $c = \frac{9}{4}$ 时，方程有两个相等的实数根：若将 $c$ 的值在 $\frac{9}{4}$ 的基础上减小，则此时方程根的情况是（）

A、没有实数根 B、两个相等的实数根 C、两个不相等的实数根 D、一个实数根

查看试题解析
12. 如图，正六边形 $A B C D E F$ 内接于 $⊙ O$ ，正六边形的周长是12，则 $⊙ O$ 的半径是（）

A、3 B、2 C、 $2 \sqrt{2}$ D、 $2 \sqrt{3}$

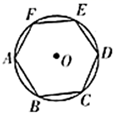查看试题解析
13. 已知锐角∠AOB如图，（1）在射线OA上取一点C，以点O为圆心，OC长为半径作 $\overset{⌢}{P Q}$ ，交射线OB于点D，连接CD；（2）分别以点C，D为圆心，CD长为半径作弧，交 $\overset{⌢}{P Q}$ 于点M，N；（3）连接OM，MN．
根据以上作图过程及所作图形，下列结论中错误的是（）

A、∠COM=∠COD B、若OM=MN，则∠AOB=20° C、MN∥CD D、MN=3CD

查看试题解析
14. 定义新运算：对于两个不相等的实数a，b，我们规定符号 $\max {a ， b}$ 表示a，b中的较大值，如： $\max {2 ， 4} = 4$ ．因此， $\max {- 2 ， - 4} = - 2$ ；按照这个规定，若 $\max {x ， - x} = \frac{x^{2} - 3 x - 2}{2}$ ，则x的值是（）

A、－1 B、－1或 $\frac{5 + \sqrt{33}}{2}$ C、 $\frac{5 + \sqrt{33}}{2}$ D、1或 $\frac{5 - \sqrt{33}}{2}$

查看试题解析
15. 如图所示，抛物线 $y = a x^{2} + b x + c$ 的顶点为 $B (- 1 ， 3)$ ，与 $x$ 轴的交点 $A$ 在点 $(- 3 ， 0)$ 和 $(- 2 ， 0)$ 之间，以下结论：① $b^{2} - 4 a c = 0$ ；② $a + b + c > 0$ ；③ $2 a - b = 0$ ；④ $c - a = 3$ ．其中正确的是（）

A、①② B、③④ C、②③ D、①③

查看试题解析
16. 如图1，图2是甲、乙两位同学设置的“数值转换机”的示意图，若输入的 $m = - 2$ ，则输出的结果分别为（）

A、9，23 B、23，9 C、9，29 D、29，9

查看试题解析

二、填空题

17. 为估计某水库鲢鱼的数量，养鱼户李老板先捞上150条鲢鱼并在鲢鱼身上做红色的记号，然后立即将这150条鲢鱼放回水库中，一周后，李老板又捞取200条鲢鱼，发现带红色记号的鱼有三条，据此可估计出该水库中鲢鱼约有条．

查看试题解析
18. 一男生推铅球，铅球行进高度y与水平距离x之间的关系是 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，则铅球推出的距离是.此时铅球行进高度是.

查看试题解析
19. 张老师在讲解复习《圆》的内容时，用投影仪屏幕展示出如下内容：
如图， $Δ A B C$ 内接于 $⊙ O$ ，直径 $A B$ 的长为2，过点C的切线交 $A B$ 的延长线于点D．

张老师让同学们添加条件后，编制一道题目，并按要求完成下列填空．

(1)、在屏幕内容中添加条件 $∠ D = 30 °$ ，则 $A D$ 的长为．

(2)、以下是小明、小聪的对话：
小明：我加的条件是 $B D = 1$ ，就可以求出 $A D$ 的长

小聪：你这样太简单了，我加的是 $∠ A = 30 °$ ，连结 $O C$ ，就可以证明 $Δ A B C$ 与 $Δ D C O$ 全等．

参考上面对话，在屏幕内容中添加条件，编制一道题目（此题目不解答，可以添线、添字母）．．

查看试题解析

三、解答题

20. 如图，在平面直角坐标系中， $Δ A B C$ 的三个顶点坐标分别为 $A (- 2 ， - 1)$ 、 $B (- 1 ， 1)$ 、 $C (0 ， - 2)$ ．

(1)、点 $B$ 关于坐标原点 $O$ 对称的点的坐标为；

(2)、将 $Δ A B C$ 绕着点 $C$ 顺时针旋转 $90 °$ ，画出旋转后得到的 $Δ A_{1} B_{1} C$ ；

(3)、在（2）中，求边 $C A$ 所扫过区域的面积是多少？（结果保留 $π$ ）．

(4)、若 $A$ 、 $B$ 、 $C$ 三点的横坐标都加3，纵坐标不变，图形 $Δ A B C$ 的位置发生怎样的变化？

查看试题解析
21. 我市某童装专卖店在销售中发现，一款童装每件进价为40元，若销售价为60元，每天可售出20件，为迎接“双十一”，专卖店决定采取适当的降价措施，以扩大销售量，经市场调查发现，如果每件童装降价1元，那么平均可多售出2件 $.$ 设每件童装降价x元 $(x > 0)$ 时，平均每天可盈利y元．

(1)、写出y与x的函数关系式；

(2)、当该专卖店每件童装降价多少元时，平均每天盈利400元？

(3)、该专卖店要想平均每天盈利600元，可能吗？请说明理由．

查看试题解析
22. 文具店有三种品牌的6个笔记本，价格是4，5，7（单位：元）三种，从中随机拿出一个本，已知 $P$ （一次拿到7元本） $= \frac{2}{3}$ ．

(1)、求这6个本价格的众数．

(2)、若琪琪已拿走一个7元本，嘉嘉准备从剩余5个本中随机拿一个本．
①所剩的5个本价格的中位数与原来6个本价格的中位数是否相同？并简要说明理由；

②嘉嘉先随机拿出一个本后不放回，之后又随机从剩余的本中拿一个本，用列表法求嘉嘉两次都拿到7元本的概率．

查看试题解析
23. 如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图，图中 $O P$ 为下水管道口直径， $O B$ 为可绕转轴 $O$ 自由转动的阀门，平时阀门被管道中排出的水冲开，可排出城市污水：当河水上涨时，阀门会因河水压迫而关闭，以防止河水倒灌入城中．若阀门的直径 $O B = O P = 100 cm$ ， $O A$ 为检修时阀门开启的位置，且 $O A = O B$ ．

(1)、直接写出阀门被下水道的水冲开与被河水关闭过程中 $∠ P O B$ 的取值范围；

(2)、为了观测水位，当下水道的水冲开阀门到达 $O B$ 位置时，在点 $A$ 处测得俯角 $∠ C A B = 67.5 °$ ，若此时点 $B$ 恰好与下水道的水平面齐平，求此时下水道内水的深度．（结果保留根号）

查看试题解析
24. 如图，一次函数 $y=kx+b(k \neq 0)$ 的图象与反比例函数 $y = \frac{m}{x} (m \neq 0)$ 的图象交于二、四象限内的A、B两点，与x轴交于C点，点A的坐标为（- 3，4），点B的坐标为(6，n).

(1)、求该反比例函数和一次函数的解析式；

(2)、连接OB，求△AOB 的面积；

(3)、在x轴上是否存在点P ，使△APC是直角三角形. 若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析
25. 如图，已知 $A B = 10$ ，以 $A B$ 为直径作半圆 $O$ ，半径 $O A$ 绕点 $O$ 顺时针旋转得到 $O C$ ，点 $A$ 的对应点为 $C$ ，当点 $C$ 与点 $B$ 重合时停止．连接 $B C$ 并延长到点 $D$ ，使得 $C D = B C$ ，过点 $D$ 作 $D E ⊥ A B$ 于点 $E$ ，连接 $A D$ ， $A C$ ．

(1)、 $A D =$ ；

(2)、如图，当点 $E$ 与点 $O$ 重合时，判断 $Δ A B D$ 的形状，并说明理由；

(3)、如图，当 $O E = 1$ 时，求 $B C$ 的长；

(4)、如图，若点 $P$ 是线段 $A D$ 上一点，连接 $P C$ ，当 $P C$ 与半圆 $O$ 相切时，直接写出直线 $P C$ 与 $A D$ 的位置关系．

查看试题解析
26. 如图，已知抛物线 $y = - x^{2} + b x + c$ 与 $x$ 轴交于 $A$ 、 $B$ 两点， $A B = 4$ ，交 $y$ 轴于点 $C$ ，对称轴是直线 $x = 1$ ．

(1)、求抛物线的解析式及点 $C$ 的坐标；

(2)、连接 $B C$ ， $E$ 是线段 $O C$ 上一点， $E$ 关于直线 $x = 1$ 的对称点 $F$ 正好落在 $B C$ 上，求点 $F$ 的坐标；

(3)、动点 $M$ 从点 $O$ 出发，以每秒2个单位长度的速度向点 $B$ 运动，过 $M$ 作 $x$ 轴的垂线交抛物线于点 $N$ ，交线段 $B C$ 于点 $Q$ ．设运动时间为 $t$ （ $t > 0$ ）秒．若 $Δ A O C$ 与 $Δ B M N$ 相似，请求出 $t$ 的值．

查看试题解析