河北省衡水市饶阳县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-05 类型:期末考试
一、单选题
-
1. 下列各点中,在函数y=- 图象上的是( )A、(﹣2,4) B、(2,4) C、(﹣2,﹣4) D、(8,1)2. 已知△ABC∽△DEF,若△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积之比为( )
A、4:3 B、3:4 C、16:9 D、9:163. 点A(1,y1)、B(3,y2)是反比例函数y= 图象上的两点,则y1、y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、不能确定4. 如图,E是▱ABCD的边BC的延长线上一点,连接AE交CD于F , 则图中共有相似三角形( ) A、4对 B、3对 C、2对 D、1对5. 如图,点A是反比例函数 图象上任意一点, 轴于B,点C是x轴上的动点,则 的面积为( )
A、4对 B、3对 C、2对 D、1对5. 如图,点A是反比例函数 图象上任意一点, 轴于B,点C是x轴上的动点,则 的面积为( ) A、1 B、2 C、4 D、不能确定6. 如图,下列条件不能判定△ADB∽△ABC的是( )
A、1 B、2 C、4 D、不能确定6. 如图,下列条件不能判定△ADB∽△ABC的是( )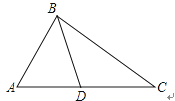 A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、7. 如图,在 中,点D、E、F分别在边 、 、 上,且 , ,若 ,则 的值为( )
A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、7. 如图,在 中,点D、E、F分别在边 、 、 上,且 , ,若 ,则 的值为( ) A、 B、 C、 D、8. 如图,双曲线y=与直线y=﹣x交于A、B两点,且A(﹣2,m),则点B的坐标是( )
A、 B、 C、 D、8. 如图,双曲线y=与直线y=﹣x交于A、B两点,且A(﹣2,m),则点B的坐标是( ) A、(2,﹣1) B、(1,﹣2) C、( , ﹣1) D、(﹣1,)9. 如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
A、(2,﹣1) B、(1,﹣2) C、( , ﹣1) D、(﹣1,)9. 如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( ) A、 B、 C、 D、10. 如图,在△ABC中,点E,F分别在边AB,AC上,EF∥BC, ,△CEF的面积为2,则△EBC的面积为( )
A、 B、 C、 D、10. 如图,在△ABC中,点E,F分别在边AB,AC上,EF∥BC, ,△CEF的面积为2,则△EBC的面积为( ) A、4 B、6 C、8 D、1211. 如图, 是直角三角形, , ,点A在反比例函数 的图象上.若点B在反比例函数 的图象上,则k的值为( )
A、4 B、6 C、8 D、1211. 如图, 是直角三角形, , ,点A在反比例函数 的图象上.若点B在反比例函数 的图象上,则k的值为( ) A、2 B、-2 C、4 D、-412. 在四边形 ABCD 中,∠B=90°,AC=4,AB∥CD,DH 垂直平分AC,点 H 为垂足,设 AB=x,AD=y,则y 关于x 的函数关系用图象大致可以表示为 ( )
A、2 B、-2 C、4 D、-412. 在四边形 ABCD 中,∠B=90°,AC=4,AB∥CD,DH 垂直平分AC,点 H 为垂足,设 AB=x,AD=y,则y 关于x 的函数关系用图象大致可以表示为 ( )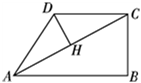 A、
A、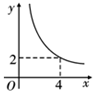 B、
B、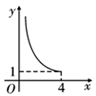 C、
C、 D、
D、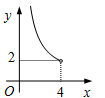 13. 如图,已知点A是双曲线y= 在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )
13. 如图,已知点A是双曲线y= 在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( ) A、n=-2m B、n=- C、n=-4m D、n=-14. 如图,△ABE和△CDE是以点E(1,0)为位似中心的位似图形,已知点A(3,4),C(2,2),D(3,1),则点D的对应点B的坐标是( )
A、n=-2m B、n=- C、n=-4m D、n=-14. 如图,△ABE和△CDE是以点E(1,0)为位似中心的位似图形,已知点A(3,4),C(2,2),D(3,1),则点D的对应点B的坐标是( )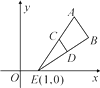 A、(4,2) B、(4,1) C、(5,2) D、(5,1)15. 如图,反比例函数 在第二象限的图象上有两点A、B,它们的横坐标分别为-1,-3.直线AB与x轴交于点C,则△AOC的面积为( )
A、(4,2) B、(4,1) C、(5,2) D、(5,1)15. 如图,反比例函数 在第二象限的图象上有两点A、B,它们的横坐标分别为-1,-3.直线AB与x轴交于点C,则△AOC的面积为( ) A、8 B、10 C、12 D、2416. 如图,在正方形ABCD中,点E为AB边的中点,点G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )
A、8 B、10 C、12 D、2416. 如图,在正方形ABCD中,点E为AB边的中点,点G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
17. 如图,在 中,D、E分别是边 、 上的点,且 ∥ ,若 与 的周长之比为 ,AD=4,则DB=.
 18. 已知反比例函数y= 的图象在第二、四象限,则m的取值范围是 .19. 甲、乙两盏路灯底部间的距离是30米,一天晚上,当小华走到距路灯乙底部5米处时,发现自己的身影顶部正好接触路灯乙的底部.已知小华的身高为1.5米,那么路灯甲的高为米.
18. 已知反比例函数y= 的图象在第二、四象限,则m的取值范围是 .19. 甲、乙两盏路灯底部间的距离是30米,一天晚上,当小华走到距路灯乙底部5米处时,发现自己的身影顶部正好接触路灯乙的底部.已知小华的身高为1.5米,那么路灯甲的高为米. 20. 如图,点E、F在函数y= 的图象上,直线EF分别与x轴、y轴交于点A、B , 且BE:BF=1:3,则△EOF的面积是 .
20. 如图,点E、F在函数y= 的图象上,直线EF分别与x轴、y轴交于点A、B , 且BE:BF=1:3,则△EOF的面积是 .
三、解答题
-
21. 在平面直角坐标系中,已知反比例函数y= 的图象经过点A(1, ).(1)、试确定此反比例函数的解析式;(2)、点O是坐标原点,将线OA绕O点顺时针旋转30°得到线段OB , 判断点B是否在此反比例函数的图象上,并说明理由.22. 如图,在平面直角坐标系中,已知 三个顶点的坐标分别为 , , .

⑴画出 绕点A顺时针旋转 后得到的 ;并写出点 , , 的坐标;
⑵以原点O为位似中心,画出将 三条边放大为原来的2倍后的 .
23. 如图,小明同学用自制的直角三角形纸板 测量树 的高度,他调整自己的位置,设法使斜边 保持水平,并且边 与点B在同一直线上.已知纸板的两条直角边 , ,测得边DF离地面的高度 , ,求树AB的高度.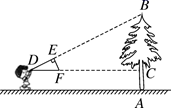 24. 如图, 是 的直径, 与 相切于点B,连接 交 于点C,连接BC.
24. 如图, 是 的直径, 与 相切于点B,连接 交 于点C,连接BC.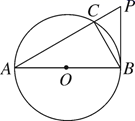 (1)、求证: ;(2)、求证: .25. 如图,在平面直角坐标系 中,反比例函数 的图象与一次函数 的图象交点为 , .
(1)、求证: ;(2)、求证: .25. 如图,在平面直角坐标系 中,反比例函数 的图象与一次函数 的图象交点为 , . (1)、求反比例函数与一次函数的解析式及B点坐标;(2)、若C是y轴上的点,且满足 的面积为10,求C点坐标.26. 心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)、求反比例函数与一次函数的解析式及B点坐标;(2)、若C是y轴上的点,且满足 的面积为10,求C点坐标.26. 心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):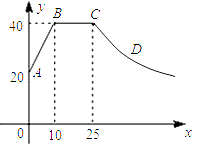 (1)、开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?(2)、一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
(1)、开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?(2)、一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?