河北省邯郸市大名县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-05 类型:期末考试
一、单选题
-
1. 服装店为了解某品牌外套销售情况,对各种码数销量进行统计店主最应关注的统计量是( )A、平均数 B、中位数 C、方差 D、众数2. 关于x的一元二次方程 根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、根的情况无法判断3. 如图,在△ABC中,点D,E分别在AB,AC边上,且DE∥BC,若AD:DB=3:2,AE=6,则EC等于( )
 A、10 B、4 C、15 D、94. 若 均为锐角,且 ,则( ).A、 B、 C、 D、5. 已知函数 是反比例函数,则此反比例函数的图象在( )A、第一、三象限 B、第二、四象限 C、第一、四象限 D、第二、三象限6. 已知 和 的半径长分别是方程 的两根,且 ,则 和 的位置关系为( )A、相交 B、内切 C、内含 D、外切7. 已知二次函数y=a(x+1)2-b(a≠0)有最小值,则a,b的大小关系为 ( )A、a>b B、a<b C、a=b D、不能确定8. 下列事件中,必然事件是( )A、 一定是正数 B、八边形的外角和等于 C、明天是晴天 D、中秋节晚上能看到月亮9. 如图,是由7个大小相同的小正方体堆砌而成的几何体,若从标有①、②、③、④的四个小正方体中取走一个后,余下几何体与原几何体的主视图相同,则取走的正方体是( )
A、10 B、4 C、15 D、94. 若 均为锐角,且 ,则( ).A、 B、 C、 D、5. 已知函数 是反比例函数,则此反比例函数的图象在( )A、第一、三象限 B、第二、四象限 C、第一、四象限 D、第二、三象限6. 已知 和 的半径长分别是方程 的两根,且 ,则 和 的位置关系为( )A、相交 B、内切 C、内含 D、外切7. 已知二次函数y=a(x+1)2-b(a≠0)有最小值,则a,b的大小关系为 ( )A、a>b B、a<b C、a=b D、不能确定8. 下列事件中,必然事件是( )A、 一定是正数 B、八边形的外角和等于 C、明天是晴天 D、中秋节晚上能看到月亮9. 如图,是由7个大小相同的小正方体堆砌而成的几何体,若从标有①、②、③、④的四个小正方体中取走一个后,余下几何体与原几何体的主视图相同,则取走的正方体是( ) A、① B、② C、③ D、④10. 如图,在 中, 是 的中点, , ,则 的长为( )
A、① B、② C、③ D、④10. 如图,在 中, 是 的中点, , ,则 的长为( ) A、 B、4 C、 D、11. 一次函数y=ax+b与反比例函数y= ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )A、
A、 B、4 C、 D、11. 一次函数y=ax+b与反比例函数y= ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )A、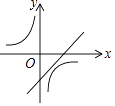 B、
B、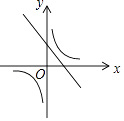 C、
C、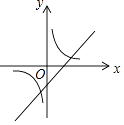 D、
D、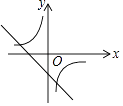 12. 如图,CD为⊙O的弦,直径AB为4,AB⊥CD于E , ∠A=30°,则扇形BOC的面积为( )
12. 如图,CD为⊙O的弦,直径AB为4,AB⊥CD于E , ∠A=30°,则扇形BOC的面积为( )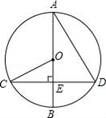 A、 B、 C、π D、13. 把抛物线y=﹣x2向右平移1个单位,再向下平移2个单位,所得抛物线是( )A、y=(x﹣1)2+2 B、y=﹣(x﹣1)2+2 C、y=﹣(x+1)2+2 D、y=﹣(x﹣1)2﹣214.
A、 B、 C、π D、13. 把抛物线y=﹣x2向右平移1个单位,再向下平移2个单位,所得抛物线是( )A、y=(x﹣1)2+2 B、y=﹣(x﹣1)2+2 C、y=﹣(x+1)2+2 D、y=﹣(x﹣1)2﹣214.如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,AD=5,BD=2,则DE的长为( )
 A、 B、 C、 D、15. 如图,从点 看一山坡上的电线杆 ,观测点 的仰角是45°,向前走 到达 点,测得顶端点 和杆底端点 的仰角分别是60°和30°,则该电线杆 的高度( )
A、 B、 C、 D、15. 如图,从点 看一山坡上的电线杆 ,观测点 的仰角是45°,向前走 到达 点,测得顶端点 和杆底端点 的仰角分别是60°和30°,则该电线杆 的高度( ) A、 B、 C、 D、16. 二次函数y=x2+bx﹣t的对称轴为x=2.若关于x的一元二次方程x2+bx﹣t=0在﹣1<x<3的范围内有实数解,则t的取值范围是( )A、﹣4≤t<5 B、﹣4≤t<﹣3 C、t≥﹣4 D、﹣3<t<5
A、 B、 C、 D、16. 二次函数y=x2+bx﹣t的对称轴为x=2.若关于x的一元二次方程x2+bx﹣t=0在﹣1<x<3的范围内有实数解,则t的取值范围是( )A、﹣4≤t<5 B、﹣4≤t<﹣3 C、t≥﹣4 D、﹣3<t<5二、填空题
-
17. 将一元二次方程 用配方法化成的 形式为 .18. 四边形 为 的内接四边形, 为 的直径, 为 延长线上一点, 为 的切线,若 ,则 .若 ,则 .
 19. 抛物线y=(m2-2)x2-4mx+n的对称轴是x=2,且它的最高点在直线y= x+2上,则m=,n=.
19. 抛物线y=(m2-2)x2-4mx+n的对称轴是x=2,且它的最高点在直线y= x+2上,则m=,n=.三、解答题
-
20. 已知关于x的一元二次方程x2﹣(2k+3)x+k2+3k+2=0(1)、试判断上述方程根的情况.(2)、已知△ABC的两边AB、AC的长是关于上述方程的两个实数根,BC的长为5,当k为何值时,△ABC是等腰三角形.21. 如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,AB∶BD= .
 (1)、求tan∠DAC的值.(2)、若BD=4,求S△ABC.22. “垃圾分类”越来越受到人们的关注,我市某中学对部分学生就“垃圾分类”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:
(1)、求tan∠DAC的值.(2)、若BD=4,求S△ABC.22. “垃圾分类”越来越受到人们的关注,我市某中学对部分学生就“垃圾分类”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题: (1)、接受问卷调查的学生共有人,条形统计图中m的值为;(2)、扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为;(3)、若从对垃圾分类知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加垃圾分类知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.23. 如图,正方形 、等腰 的顶点 在对角线 上(点 与 、 不重合), 与 交于 , 延长线与 交于点 ,连接 .
(1)、接受问卷调查的学生共有人,条形统计图中m的值为;(2)、扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为;(3)、若从对垃圾分类知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加垃圾分类知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.23. 如图,正方形 、等腰 的顶点 在对角线 上(点 与 、 不重合), 与 交于 , 延长线与 交于点 ,连接 . (1)、求证: .(2)、求证:(3)、若 ,求 的值.24. 如图:反比例函数 的图象与一次函数 的图象交于 、 两点,其中 点坐标为 .
(1)、求证: .(2)、求证:(3)、若 ,求 的值.24. 如图:反比例函数 的图象与一次函数 的图象交于 、 两点,其中 点坐标为 . (1)、求反比例函数与一次函数的表达式;(2)、观察图象,直接写出当 时,自变量 的取值范围;(3)、一次函数的图象与 轴交于点 ,点 是反比例函数图象上的一个动点,若 ,求此时 点的坐标.25. 已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C , 使AB=AC , 连接AC , 过点D作DE⊥AC , 垂足为 E .
(1)、求反比例函数与一次函数的表达式;(2)、观察图象,直接写出当 时,自变量 的取值范围;(3)、一次函数的图象与 轴交于点 ,点 是反比例函数图象上的一个动点,若 ,求此时 点的坐标.25. 已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C , 使AB=AC , 连接AC , 过点D作DE⊥AC , 垂足为 E . (1)、求证:DC=BD;(2)、求证:DE为⊙O的切线;(3)、若AB=12,AD=6 ,连接OD , 求扇形BOD的面积.26. 如图,在平面直角坐标系中,直线y=﹣5x+5与x轴、y轴分别交于A , C两点,抛物线y=x2+bx+c经过A , C两点,与x轴交于另一点B .
(1)、求证:DC=BD;(2)、求证:DE为⊙O的切线;(3)、若AB=12,AD=6 ,连接OD , 求扇形BOD的面积.26. 如图,在平面直角坐标系中,直线y=﹣5x+5与x轴、y轴分别交于A , C两点,抛物线y=x2+bx+c经过A , C两点,与x轴交于另一点B . (1)、求抛物线解析式及B点坐标;(2)、x2+bx+c≤﹣5x+5的解集是;(3)、若点M为抛物线上一动点,连接MA、MB , 当点M运动到某一位置时,△ABM面积为△ABC的面积的 倍,求此时点M的坐标.
(1)、求抛物线解析式及B点坐标;(2)、x2+bx+c≤﹣5x+5的解集是;(3)、若点M为抛物线上一动点,连接MA、MB , 当点M运动到某一位置时,△ABM面积为△ABC的面积的 倍,求此时点M的坐标.