河北省保定市唐县2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. “抛一枚均匀硬币，落地后正面朝上”这一事件是（　　）

A、必然事件 B、随机事件 C、确定事件 D、不可能事件

查看试题解析
2.
如图，该图形围绕点O按下列角度旋转后，不能与其自身重合的是（）

A、72°　　 B、108° C、144°　　 D、216°

查看试题解析
3. 已知反比例函数y= $\frac{k}{x}$ 的图象经过点P（﹣1，2），则这个函数的图象位于（）

A、二、三象限 B、一、三象限 C、三、四象限 D、二、四象限

查看试题解析
4. 用配方法将方程 $x^{2} - 4 x - 1 = 0$ 变形为 ${(x - 2)}^{2} = m$ ，则m的值是（）

A、4 B、5 C、6 D、7

查看试题解析
5. 在下列四个图案中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 . D、

查看试题解析
6. 一元二次方程 $x^{2} + 2020 = 0$ 的根的情况是(　　)

A、有两个相等的实根 B、有两个不等的实根 C、只有一个实根 D、无实数根

查看试题解析
7. 如图，在正方形网格上有两个相似三角形△ABC和△DEF，则∠BAC的度数为（）

A、105° B、115° C、125° D、135°

查看试题解析
8. 已知三角形的面积一定，则它底边a上的高h与底边a之间的函数关系的图象大致是（　　）

A、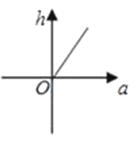 B、 C、 D、

查看试题解析
9. 下列对二次函数y=x²﹣x的图象的描述，正确的是（）

A、开口向下 B、对称轴是y轴 C、经过原点 D、在对称轴右侧部分是下降的

查看试题解析
10. 参加一次聚会的每两人都握了一次手，所有人共握手10次，若共有x人参加聚会，则根据题意，可列方程（　）

A、 $x (x - 1) = 10$ B、 $x (x + 1) = 10$ C、 $\frac{1}{2} x (x - 1) = 10$ D、 $\frac{1}{2} x (x + 1) = 10$

查看试题解析
11. 一元钱硬币的直径约为24mm，则用它能完全覆盖住的正六边形的边长最大不能超过（　　）

A、12mm B、12 $\sqrt{3}$ mm C、6mm D、6 $\sqrt{3}$ mm

查看试题解析
12. 如图，一圆弧过方格的格点A、B、C，在方格中建立平面直角坐标系，使点A的坐标为（﹣3，2），则该圆弧所在圆心坐标是（）

A、（0，0） B、（﹣2，1） C、（﹣2，﹣1） D、（0，﹣1）

查看试题解析
13. 用一个圆心角为120°，半径为4的扇形作一个圆锥的侧面．则这个圆锥的底面圆的半径为（）

A、 $\frac{4}{3}$ B、1 C、 $\frac{3}{4}$ D、2

查看试题解析
14. 如图，AB是⊙O的直径，BT是⊙O的切线，若∠ATB=45°，AB=2，则阴影部分的面积是（）

A、2 B、1 C、 $\frac{3}{2} - \frac{1}{4} π$ D、 $\frac{1}{2} + \frac{1}{4} π$

查看试题解析
15. 如图，将Rt△ABC平移到△A′B′C′的位置，其中∠C＝90°，使得点C′与△ABC的内心重合，已知AC＝4，BC＝3，则阴影部分的周长为（）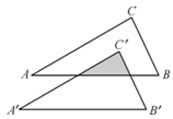

A、5 B、6 C、7 D、8

查看试题解析
16. 如图，在平面直角坐标系中，已知点A的坐标是 $(0 ， 2)$ ，点P是曲线 $y = \frac{k}{x} (x > 0)$ 上的一个动点，作 $P B ⊥ x$ 轴于点B，当点P的橫坐标逐渐减小时，四边形 $O A P B$ 的面积将会（）

A、逐渐增大 B、不变 C、逐渐减小 D、先减小后增大

查看试题解析

二、填空题

17. 已知△ABC ， D、E分别在AC、BC边上，且DE∥AB ， CD＝2，DA＝3，△CDE面积是4，则△ABC的面积是

查看试题解析
18. 把一个小球以20米/秒的速度竖直向上弹出，它在空中的高度h（米）与时间t（秒），满足关系：h=20t-5t² ，当小球达到最高点时，小球的运动时间为第秒时．

查看试题解析
19. 如图，六边形ABCDEF是正六边形，曲线FK₁K₂K₃K₄K₅K₆K₇…叫做“正六边形的渐开线”，其中弧FK₁、弧K₁K₂、弧K₂K₃、弧K₃K₄、弧K₄K₅、弧K₅K₆、…的圆心依次按点A、B、C、D、E、F循环，其弧长分别为l₁、l₂、l₃、l₄、l₅、l₆、…．当AB＝1时，l₃= ， l₂₀₁₉＝．

查看试题解析

三、解答题

20. 解方程

(1)、 $x^{2} + 4 x - 1 = 0$

(2)、 $(x - 1) (x + 1) = x + 1$

查看试题解析
21. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，1），B（﹣1，4），C（﹣3，2）

⑴画出△ABC关于点B成中心对称的图形△A₁BC₁；

⑵以原点O为位似中心，位似比为1：2，在y轴的左侧画出△ABC放大后的图形△A₂B₂C₂ ，并直接写出C₂的坐标．

查看试题解析
22. 有A、B、C₁、C₂四张同样规格的硬纸片，它们的背面完全一样，正面如图1所示．将它们背面朝上洗匀后，随机抽取并拼图．

(1)、填空：随机抽出一张，正面图形正好是中心对称图形的概率是．

(2)、随机抽出两张(不放回)，其图形可拼成如图2的四种图案之一．请你用画树状图或列表的方法，分析拼成哪种图案的概率最大？

查看试题解析
23. 如图，△OAB中，OA＝OB＝10cm ， ∠AOB＝80°，以点O为圆心，半径为6cm的优弧 $\overset{⌢}{M N}$ 分别交OA、OB于点M、N ．

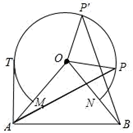(1)、点P在右半弧上(∠BOP是锐角)，将OP绕点O逆时针旋转80°得OP′．求证：AP＝BP′；

(2)、点T在左半弧上，若AT与圆弧相切，求AT的长．

(3)、Q为优弧上一点，当△AOQ面积最大时，请直接写出∠BOQ的度数为．

查看试题解析
24.
如图，一次函数y=kx+b（k≠0）与反比例函数y= $\frac{m}{x}$ （m≠0）的图象有公共点A（1，a）、D（﹣2，﹣1）．直线l与x轴垂直于点N（3，0），与一次函数和反比例函数的图象分别交于点B、C．

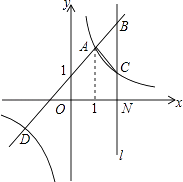(1)、求一次函数与反比例函数的解析式；

(2)、根据图象回答，x在什么范围内，一次函数的值大于反比例函数的值；

(3)、求△ABC的面积．

查看试题解析
25. 若抛物线 $L ： y = a x^{2} + b x + c$ （a、b、c是常数， $a b c \neq 0$ ）与直线l都经过y轴上的一点P，且抛物线L的顶点Q在直线l上，则称此直线 $l$ 与该抛物线L具有“一带一路”关系，此时，直线l叫做抛物线L的“带线”，抛物线L叫做直线l的“路线”．

(1)、若直线 $y = m x + 1$ 与抛物线 $y = x^{2} - 2 x + n$ 具有“一带一路”关系，求m、n的值．

(2)、若某“路线”L的顶点在反比例函数 $y = \frac{6}{x}$ 的图象上，它的“带线” 的解析式为 $y = 2 x - 4$ ，求此路的解析式．

查看试题解析
26. 某商场秋季计划购进一批进价为每件40元的T恤进行销售．

(1)、根据销售经验，应季销售时，若每件T恤的售价为60元，可售出400件；若每件T恤的售价每提高1元，销售量相应减少10件．
假设每件T恤的售价提高x元，那么销售每件T恤所获得的利润是元，销售量是件(用含x的代数式表示)；

(2)、设应季销售利润为y元，请写y与x的函数关系式；并求出应季销售利润为8000元时每件T恤的售价．

(3)、根据销售经验，过季处理时，若每件T恤的售价定为30元亏本销售，可售出50件；若每件T恤的售价每降低1元，销售量相应增加5条，
①若剩余100件T恤需要处理，经过降价处理后还是无法销售的只能积压在仓库，损失本金；若使亏损金额最小，每件T恤的售价应是多少元？

②若过季需要处理的T恤共m件，且100≤m≤300，过季亏损金额最小是（）元(用含m的代数式表示)．（注：抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 顶点是 $(- \frac{b}{2 a} ， \frac{4 a c - b^{2}}{4 a})$ ）

查看试题解析