河北省保定市定州市2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程x²﹣3x﹣4＝0的一次项系数是（　　）

A、1 B、﹣3 C、3 D、﹣4

查看试题解析
2. 点 $P (4 ， - 3)$ 关于原点的对称点是 $($ $)$

A、 $(4 ， 3)$ B、 $(- 3 ， 4)$ C、 $(- 4 ， 3)$ D、 $(3 ， - 4)$

查看试题解析
3. 下列成语表示随机事件的是（）

A、水中捞月 B、水滴石穿 C、瓮中捉鳖 D、守株待兔

查看试题解析
4. 下列四个点中，在反比例函数y＝ $\frac{- 6}{x}$ 的图象上的是（　　）

A、（﹣3，﹣2） B、（3，2） C、（﹣2，3） D、（﹣2，﹣3）

查看试题解析
5. 若 $\frac{x}{2} = \frac{y}{7} = \frac{z}{5}$ ，则 $\frac{x + y - z}{x}$ 的值是（　　）

A、1 B、2 C、3 D、4

查看试题解析
6. 如图，⊙O是△ABC的外接圆，∠OCB＝40°，则∠A的大小为（）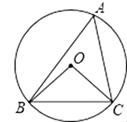

A、40° B、50° C、80° D、100°

查看试题解析
7. 给出下列函数，其中y随x的增大而减小的函数是（）
①y＝2x；②y＝﹣2x+1；③y＝ $\frac{2}{x}$ （x＜0）；④y＝x²（x＜1）．

A、①③④ B、②③④ C、②④ D、②③

查看试题解析
8. 如图，将△ABC绕点A逆时针旋转100°，得到△ADE．若点D在线段BC的延长线上，则 $∠ B$ 的大小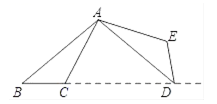为（）

A、30° B、40° C、50° D、60°

查看试题解析
9. 如图，点O是△ABC内一点、分别连接OA、OB、OC并延长到点D、E、F，使AD＝2OA，BE＝2OB，CF＝2OC，连接DE，EF，FD．若△ABC的面积是3，则阴影部分的面积是（　　）

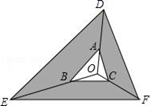A、6 B、15 C、24 D、27

查看试题解析
10. 在平面直角坐标系xOy中，以点(3，4)为圆心，4为半径的圆与y轴(　　)

A、相交 B、相切 C、相离 D、无法确定

查看试题解析
11. 已知x₁ ， x₂是关于x的方程x²＋ax－2b＝0的两个实数根，且x₁＋x₂＝－2，x₁·x₂＝1，则b^a的值是（）

A、 $\frac{1}{4}$ B、－ $\frac{1}{4}$ C、4 D、－1

查看试题解析
12. 如图，AB是半圆O的直径，AC为弦，OD⊥AC于D，过点O作OE∥AC交半圆O于点E，过点E作EF⊥AB于F．若AC=2，则OF的长为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、1 D、2

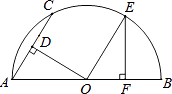查看试题解析
13. 如图，在正方形网格上有两个相似三角形△ABC和△DEF，则∠BAC的度数为（）

A、105° B、115° C、125° D、135°

查看试题解析
14. 如图，正方形ABCD的顶点C、D在x轴上，A、B恰好在二次函数y＝2x²﹣4的图象上，则图中阴影部分的面积之和为（　　）

A、6 B、8 C、10 D、12

查看试题解析
15. 如图是二次函数y＝ax²+bx+c（a≠0）的图象的一部分，给出下列命题：
①a+b+c＝0；

②b＞2a；

③ax²+bx+c＝0的两根分别为﹣3和1；

④c＝﹣3a ，

其中正确的命题是（　　）

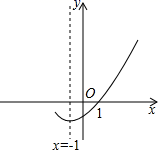A、①② B、②③ C、①③ D、①③④

查看试题解析

二、填空题

16. 某商品原售价300元，经过连续两次降价后售价为260元，设平均每次降价的百分率为x，则满足x的方程是．

查看试题解析
17. 如图，抛物线 $y = a x^{2}$ 与直线 $y = b x + c$ 的两个交点坐标分别为 $A (- 2 ， 4)$ ， $B (1 ， 1)$ ，则关于x的方程 $a x^{2} - b x - c = 0$ 的解为.

查看试题解析
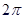18. 如图，点A、B、C在半径为9的⊙O上， $\overset{⌢}{A B}$ 的长为，则∠ACB的大小是．

查看试题解析
19. 如图，菱形ABCD的边AD与x轴平行，A、B两点的横坐标分别为1和3，反比例函数y＝ $\frac{3}{x}$ 的图象经过A、B两点，则菱形ABCD的面积是；

查看试题解析

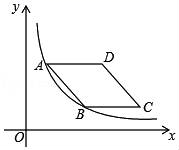
三、解答题

20. 已知关于x的一元二次方程kx²﹣4x+2＝0有两个不相等的实数根．

(1)、求实数k的取值范围；

(2)、写出满足条件的k的最大整数值，并求此时方程的根．

查看试题解析
21. 不透明的袋子中装有4个相同的小球，它们除颜色外无其它差别，把它们分别标号：1、2、3、4.

(1)、随机摸出一个小球后，放回并摇匀，再随机摸出一个，用列表或画树状图的方法求出“两次取的球标号相同”的概率；

(2)、随机摸出两个小球，直接写出“两次取出的球标号和为奇数”的概率.

查看试题解析
22. 如图，已知点A（a，3）是一次函数y₁＝x+1与反比例函数y₂＝ $\frac{k}{x}$ 的图象的交点．

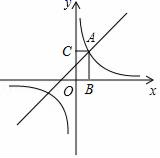(1)、求反比例函数的解析式；

(2)、在y轴的右侧，当y₁＞y₂时，直接写出x的取值范围；

(3)、求点A与两坐标轴围成的矩形OBAC的面积．

查看试题解析
23. 某山区不仅有美丽风光，也有许多令人喜爱的土特产，为实现脱贫奔小康，某村组织村民加工包装土特产销售给游客，以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x（元）与该士特产的日销售量y（袋）之间的关系如表：

x（元）

15

20

30

…

y（袋）

25

20

10

…

若日销售量y是销售价x的一次函数，试求：

(1)、日销售量y（袋）与销售价x（元）的函数关系式；

(2)、假设后续销售情况与试销阶段效果相同，要使这种土特产每日销售的利润最大，每袋的销售价应定为多少元？每日销售的最大利润是多少元？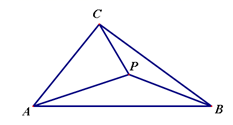

查看试题解析
24. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ， $P$ 为 $△ A B C$ 内部一点，且 $∠ A P B = ∠ B P C = 135 °$ .

(1)、求证： $△ P A B ∽ △ P B C$ ；

(2)、求证： $P A = 2 P C$ .

查看试题解析
25. 如图，AB为⊙O的直径，射线AP交⊙O于C点，∠PCO的平分线交⊙O于D点，过点D作 $D E ⊥ A P$ 交AP于E点．

(1)、求证：DE为⊙O的切线；

(2)、若DE=3，AC=8，求直径AB的长．

查看试题解析
26.
如图，在平面直角坐标系中，抛物线y=ax²+bx+c（a≠0）与y轴交与点C（0，3），与x轴交于A、B两点，点B坐标为（4，0），抛物线的对称轴方程为x=1．

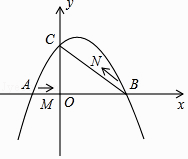(1)、求抛物线的解析式；

(2)、点M从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时点N从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，其中一个点到达终点时，另一个点也停止运动，设△MBN的面积为S，点M运动时间为t，试求S与t的函数关系，并求S的最大值；

(3)、在点M运动过程中，是否存在某一时刻t，使△MBN为直角三角形？若存在，求出t值；若不存在，请说明理由．

查看试题解析

x（元）	15	20	30	…
y（袋）	25	20	10	…