北京市通州区2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，已知Rt△ABC中，∠C＝90°，BC=3，AC=4，

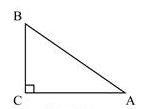
则sinA的值为（）.

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
2. 抛物线 $y = - x^{2} + 2$ 的对称轴为（）

A、 $x = 2$ B、 $x = 0$ C、 $y = 2$ D、 $y = 0$

查看试题解析
3. 如图，在 $△ ABC$ 中， $DE / / BC ， AD = 3 BD ， DE = 3$ ，则 $BC$ 的长度为（）

A、1 B、 $\frac{4}{3}$ C、 $4$ D、 $6$

查看试题解析
4. 如图，将 $⊙ O$ 沿着弦 $AB$ 翻折，劣弧恰好经过圆心O.如果半径为4，那么 $⊙ O$ 的弦 $AB$ 长度为（）

A、 $2$ B、 $4$ C、 $2 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
5. 如图， $∠ 1 = ∠ 2$ ，如果增加一个条件就能使结论 $AB \cdot DE = AD \cdot BC$ 成立，那么这个条件可以是（）

A、 $∠ C = ∠ D$ B、 $∠ B = ∠ AED$ C、 $\frac{AE}{AB} = \frac{AD}{AC}$ D、 $\frac{AE}{AC} = \frac{AD}{AB}$

查看试题解析
6. 在平面直角坐标系 $xOy$ 中，反比例函数 $y = \frac{k}{x}$ 的图象经过点(1,3)，则k的值可以为（）

A、 $- 4$ B、 $3$ C、 $- 2$ D、 $2$

查看试题解析
7. 在平面直角坐标系 $xOy$ 中，点 $A (a, b)$ 在双曲线 $y = - \frac{2}{x}$ 上，点A关于y轴的对称点B在双曲线 $y = \frac{k}{x}$ 上，则 $k - 2$ 的值为（）

A、 $- 4$ B、 $0$ C、 $2$ D、 $4$

查看试题解析
8. 如图，在平面直角坐标系 $xOy$ 中，点 $A (- 2 ， - 2) ， B (0 ， 3) ， C (3 ， 3) ， D (4 ， - 2)$ ，y是关于x的二次函数，抛物线 $y_{1}$ 经过点 $A ， B ， C$ .抛物线 $y_{2}$ 经过点 $B ， C ， D ，$ 抛物线 $y_{3}$ 经过点 $A ， B ， D ，$ 抛物线 $y_{4}$ 经过点 $A ， C ， D ，$ 则下列判断：

①四条抛物线的开口方向均向下；

②当 $x < 0$ 时，四条抛物线表达式中的y均随x的增大而增大；

③抛物线 $y_{1}$ 的顶点在抛物线 $y_{2}$ 顶点的上方；

④抛物线 $y_{4}$ 与y轴交点在点B的上方.

其中正确的是（）

A、①②④ B、①③④ C、①②③ D、②③④

查看试题解析

二、填空题

9. 抛物线 $y = - {(x + 1)}^{2}$ 的顶点坐标为.

查看试题解析
10. 写出一个过原点的二次函数表达式，可以为.

查看试题解析
11. 如图，在 $⊙ O$ 中，A，B，C是 $⊙ O$ 上三点，如果 $∠ AOB = 74 °$ ，那么 $∠ C$ 的度数为.

查看试题解析
12. 如图，根据图示，求得x和y的值分别为.

查看试题解析
13. 如图，在 $Rt Δ ABC$ 中， $∠ C = 90 ° ， ∠ A = α ， AC = b ，$ 则AB的长为（用含α和b的代数式表示）

查看试题解析
14. 如图， $AB$ 是以点O为圆心的圆形纸片的直径，弦 $CD ⊥ AB$ 于点E， $AB = 10 ， BE = 3$ .将阴影部分沿着弦 $AC$ 翻折压平，翻折后，弧 $AC$ 对应的弧为G，则点O与弧G所在圆的位置关系为.

查看试题解析
15. 已知关于x的二次函数 $y = {ax}^{2} + bx + 4$ 的图象如图所示，则关于x的方程 ${ax}^{2} + bx = 0$ 的根为

查看试题解析
16. 如图，在平面直角坐标系 $xOy$ 中，以点 $M (4 ， 3)$ 为圆心画圆，与x轴交于 $A ， B$ ；两点，与y轴交于 $C ， D$ 两点，当 $6 < CD < 8 \sqrt{3}$ 时， $sin ∠ MAB$ 的取值范围是.

查看试题解析

三、解答题

17. 计算： $| - \sqrt{3} | - {(4 - π)}^{0} - 2 \sin 60^{\circ} + （ \frac{1}{4} ）^{- 1}$ .

查看试题解析
18. 如图，在 $Rt △ ABC$ 中， $∠ ACB = 90 ° ， CD ⊥ AB$ 于点D.若 $AD = 4 ， BD = 2$ ，求 $tanA$ 的值.

查看试题解析
19. 把二次函数表达式 $y = x^{2} - 4 x + c$ 化为 $y = {(x - h)}^{2} + k$ 的形式.

查看试题解析
20. 如图，在正方形网格上有 $△ ABC$ 以及一条线段 $DE$ .请你以 $DE$ 为一条边.以正方形网格的格点为顶点画一个 $△ DEF$ ，使得 $△ ABC$ 与 $△ DEF$ 相似，并求出这两个三角形的相似比.

查看试题解析
21. 已知某二次函数图象上部分点的横坐标 $x$ 、纵坐标 $y$ 的对应值如下表.求此函数表达式.

查看试题解析
22. 将矩形纸片 $ABCD$ 沿 $AE$ 翻折，使点B落在线段 $DC$ 上，对应的点为F，若 $AE = 5 \sqrt{5} ， tan ∠ EFC = \frac{3}{4}$ ，求 $AB$ 的长.

查看试题解析
23. 如图：在平面直角坐标系 $xOy$ 中，点 $A (- 2 ， 2) ， B (4.4)$ .

(1)、尺规作图：求作过 $A ， B ， O$ 三点的圆；

(2)、设过 $A ， B ， O$ 三点的圆的圆心为M，利用网格，求点M的坐标；

(3)、若直线 $x = a$ 与 $⊙ M$ 相交，直接写出a的取值范围.

查看试题解析
24. 已知：点 $A (- 1 ， - 4)$ 和P是一次函数 $y = kx + b$ 与反比例函数 $y = \frac{m}{x}$ 图象的连个不同交点，点P关于y轴的对称点为 $P'$ ，直线 $AP$ 以及 $AP’$ 分别与x轴交于点M和N.

(1)、求反比例函数 $y = \frac{m}{x}$ 的表达式；

(2)、若 $PP' \geq \frac{3}{2} MN$ ，求k的取值范围.

查看试题解析

25. 如图，在钝角

△ ABC

中，点P为

BC

上的一个动点，连接

PA

，将射线

PA

绕点P逆时针旋转

60 °

，交线段

AB

于点D. 已知∠C=30°，CA=2

\sqrt{3}

cm，BC=7cm，设B，P两点间的距离为xcm，A，D两点间的距离ycm.

小牧根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究.下面是小牧探究的过程，请补充完整：

(1)、根据图形.可以判断此函数自变量x的取值范围是；

(2)、通过取点、画图、测量，得到了x与y的几组值，如下表：

$x / cm$	$\cdot \cdot \cdot$	0.51	1.02	1.91	3.47	3	4.16	4.47	$\cdot \cdot \cdot$
$y / cm$	$\cdot \cdot \cdot$	3.97	3.22	2.42	1.66	a	2.02	2.50	$\cdot \cdot \cdot$

通过测量。可以得到a的值为；

(3)、在平而直角坐标系xOy中.描出上表中以各对对应值为坐标的点，画出该函数的图象；

(4)、结合画出的函数图象，解决问题：当AD=3.5cm时，BP的长度约为cm.

查看试题解析

26. 在平面直角坐标系 $xOy$ 中，存在抛物线 $y = {mx}^{2} + 2$ 以及两点 $A (- 3 ， m)$ 和 $B (1 ， m)$ .

(1)、求该抛物线的顶点坐标；

(2)、若该抛物线经过点 $A (- 3. m)$ ，求此抛物线的表达式；

(3)、若该抛物线与线段 $AB$ 只有一个公共点，结合图象，求m的取值范围.

查看试题解析
27. 如图， $MO ⊥ NO$ 于点O， $△ OAB$ 为等腰直角三角形， $∠ OAB = 90 °$ ，当 $△ OAB$ 绕点O旋转时，记 $∠ MOA = a (0 ° \leq a \leq 90 °) 。 OA = 5$ .

(1)、过点B作 $BC ⊥ ON$ 交射线 $ON$ 于点C，作射线 $CA$ 交射线 $OM$ 于点D.
①依题意补全图形，求 $∠ ODC$ 的度数；

②当 $sina = \frac{4}{5}$ 时，求 $OD$ 的长.

(2)、若 $ON$ 上存在一点P，且 $OP = 10$ ，作射线 $PB$ 交射线 $OM$ 于点Q，直接写出 $QP$ 长度的最大值.

查看试题解析
28. 如图，在平面内。点Q为线段 $AB$ 上任意一点.对于该平面内任意的点P，若满足 $PQ$ 小于等于 $AB$ 则称点P为线段 $AB$ 的“限距点”.

(1)、在平面直角坐标系 $xOy$ 中，若点 $A （ - 1 ， 0 ）， B （ 1 ， 0 ）$ .
①在的点 $C （ 0 ， 2 ）， D （ - 2 ， - 2 ）， E （ 0 ， - \sqrt{3} ）$ 中，是线段 $AB$ 的“限距点”的是（）；

②点P是直线 $y = \frac{\sqrt{3}}{3} x + \frac{\sqrt{3}}{3}$ 上一点，若点P是线段AB的“限距点”，请求出点P横坐标 $x_{P}$ 的取值范围.

查看试题解析