北京市密云区2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $\frac{x}{y} = \frac{3}{4}$ ，则 $\frac{x + y}{y}$ =（）

A、 $\frac{4}{7}$ B、 $\frac{7}{4}$ C、 $\frac{3}{7}$ D、 $\frac{7}{3}$

查看试题解析
2. 二次函数 $y = x^{2} - 2$ 图像的顶点坐标为（）

A、(0，-2) B、(-2，0) C、(0，2) D、(2，0)

查看试题解析
3. 在Rt△ABC中，∠C＝90°，若 $\sin A = \frac{1}{2}$ ，则∠B的度数是（）

A、30° B、45° C、60° D、75°

查看试题解析
4. 在数轴上，点A所表示的实数为3，点B所表示的实数为a，⊙A的半径为2，下列说法中错误的是（）

A、当1<a<5时，点B在⊙A内 B、当a<5时，点B在⊙A内 C、当a<1时，点B在⊙A外 D、当a>5时，点B在⊙A外

查看试题解析
5. 如图所示，在边长为1的小正方形网格中，两个三角形是位似图形，则它们的位似中心是（）

A、点O B、点P C、点M D、点N

查看试题解析
6. 已知反比例函数的表达式为 $y = \frac{k + 2}{x}$ ，它的图象在各自象限内具有 y随x的增大而增大的特点，则k的取值范围是（）．

A、k>-2 B、 $k \geq - 2$ C、 $k < - 2$ D、 $k \leq - 2$

查看试题解析
7. 如图，在⊙O中，弦BC // OA ， AC与OB相交于点M ， ∠C=20°，则∠MBC的度数为（）．

A、30° B、40° C、50° D、60°

查看试题解析
8. 如图，矩形ABCD是由三个全等矩形拼成的，AC与DE、EF、FG、HG、HB分别交于点P、Q、K、M、N ，设△EPQ、△GKM、△BNC的面积依次为S₁、S₂、S₃ ．若S₁+S₃=30，则S₂的值为（）．

A、6 B、8 C、10 D、12

查看试题解析

二、填空题

9. 如图，直线a // b // c ，点B是线段AC的中点，若DE=2，则DF的长度为．

查看试题解析
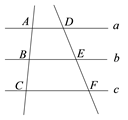10. 若边长为2的正方形内接于⊙O ，则⊙O的半径是．

查看试题解析

11. 在二次函数中

y = a x^{2} + b x + c (a \neq 0)

，y与x的部分对应值如下表：

x	......	-1	0	1	2	3	4	......
y	......	-7	-2	m	n	-2	-7	......

则m、n的大小关系为mn ．（填“>”,“=”或“<”）

查看试题解析

12.
如图，边长为1的小正方形构成的网格中，半径为1的⊙O在格点上，则∠AED的正切值为．

查看试题解析
13. 如图，铁道口的栏杆短臂长1m ，长臂长16m ．当短臂端点下降0.5m时，长臂端点升高

查看试题解析
14. 如图，反比例函数 $y = \frac{k}{x}$ 的图象位于第一、三象限，且图象上的点与坐标轴围成的矩形面积为2，请你在第三象限的图象上取一个正确的点，并写出它的坐标．

查看试题解析
15. 如图，矩形ABCD中，AB=1，AD= $\sqrt{2}$ ．以A为圆心，AD的长为半径做弧交BC边于点E ，则图中 $\overset{⌢}{D E}$ 的弧长是.

查看试题解析
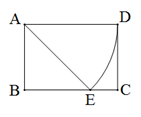16. 已知：∠BAC ．

⑴如图，在平面内任取一点O；

⑵以点O为圆心，OA为半径作圆，交射线AB于点D ，交射线AC于点E；

⑶连接DE ，过点O作线段DE的垂线交⊙O于点P；

⑷连接AP ， DP和PE ．根据以上作图过程及所作图形，下列四个结论中：

①△ADE是⊙O的内接三角形； ② $\overset{⌢}{A D} = \overset{⌢}{D P} = \overset{⌢}{P E}$ ；

③ DE=2PE； ④ AP平分∠BAC ．

所有正确结论的序号是．

查看试题解析

三、解答题

17. 计算： $\sqrt{9} + {(\frac{1}{2})}^{- 1} - \sqrt{2} \sin 45^{°} + {(\sqrt{3} - 2)}^{0}$ ．

查看试题解析
18. 已知：在△ABC中，点D、点E分别在边AB、AC上，且DE // BC ， BE平分∠ABC ．

(1)、求证：BD=DE；

(2)、若AB=10，AD=4，求BC的长．

查看试题解析
19. 已知二次函数y = x² -4x + 3．

(1)、用配方法将y = x² -4x + 3化成y = a(x - h)²+ k的形式；

(2)、在平面直角坐标系xOy中，画出该函数的图象．

(3)、结合函数图象，直接写出y＜0时自变量x的取值范围．

查看试题解析
20.
已知：如图，在⊙O中，弦AB，CD交于点E，AD=CB．求证：AE=CE．

查看试题解析
21. 已知：在△ABC中，AB=AC ， AD⊥BC于点D ，分别过点A和点C作BC、AD边的平行线交于点E ．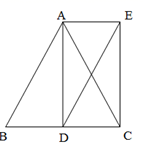

(1)、求证：四边形ADCE是矩形；

(2)、连结BE，若 $\cos ∠ A B D = \frac{1}{2}$ ，AD= $2 \sqrt{3}$ ，求BE的长．

查看试题解析
22. 某次足球比赛，队员甲在前场给队友乙掷界外球．如图所示：已知两人相距8米，足球出手时的高度为2.4米，运行的路线是抛物线，当足球运行的水平距离为2米时，足球达到最大高度4米．请你根据图中所建坐标系，求出抛物线的表达式．

查看试题解析
23. 在平面直角坐标系中，直线 y = x与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象交于点A（2，m）.

(1)、求m和k的值；

(2)、点P（x_P ， y_P）是函数 $y = \frac{k}{x} (x > 0)$ 图象上的任意一点，过点P作平行于x轴的直线，交直线y=x于点B.
①当y_P = 4时，求线段BP的长；

②当BP $\geq$ 3时，结合函数图象，直接写出点P 的纵坐标y_P的取值范围．

查看试题解析
24. 已知：如图，⊙O的直径AB与弦CD相交于点E ，且E为CD中点，过点B作CD的平行线交弦AD的延长线于点F .

(1)、求证：BF是⊙O的切线；

(2)、连结BC ，若⊙O的半径为2，tan∠BCD= $\frac{3}{4}$ ，求线段AD的长．

查看试题解析
25. 如图，点E是矩形ABCD对角线AC上的一个动点（点E可以与点A和点C重合），连接BE ．已知AB=3cm ， BC=4cm ．设A、E两点间的距离为xcm ， BE的长度为ycm ．

某同学根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行探究．

下面是该同学的探究过程，请补充完整：

(1)、通过取点、画图、测量及分析，得到了x与y的几组值，如下表：

说明：补全表格时相关数值保留一位小数）

(2)、建立平面直角坐标系，描出已补全后的表中各对对应值为坐标的点，画出该函数的图象．

(3)、结合画出的函数图象，解决问题：当BE=2AE时，AE的长度约为cm ．（结果保留一位小数）

查看试题解析
26. 在平面直角坐标系xOy中，抛物线 $y = a x^{2} - 2 a x + 5 a + 8$ （ $a \neq 0$ ）．

(1)、写出抛物线顶点的纵坐标（用含a的代数式表示）；

(2)、若该抛物线与x轴的两个交点分别为点A和点B，且点A在点B的左侧，AB=4．
①求a的值；

②记二次函数图象在点A，B之间的部分为W（含点A和点B），若直线 $y = k x + b$ （ $k \neq 0$ ）经过（1，-1），且与图形W有公共点，结合函数图象，求b的取值范围．

查看试题解析
27. 已知：在Rt△ABC中，∠BAC=90°，AB=AC ，点D为BC边中点．点M为线段BC上的一个动点（不与点C，点D重合），连接AM ，将线段AM绕点M顺时针旋转90°，得到线段ME ，连接EC ．

(1)、如图1，若点M在线段BD上．
① 依据题意补全图1；

② 求∠MCE的度数．

(2)、如图2，若点M在线段CD上，请你补全图形后，直接用等式表示线段AC、CE、CM之间的数量关系．

查看试题解析
28. 在平面直角坐标系xOy中，⊙O的半径为r（r＞0）．给出如下定义：若平面上一点P到圆心O的距离d，满足 $\frac{1}{2} r \leq d \leq \frac{3}{2} r$ ，则称点P为⊙O的“随心点”．

(1)、当⊙O的半径r=2时，A（3，0），B（0，4），C（ $- \frac{3}{2}$ ，2），D（ $\frac{1}{2}$ ， $- \frac{1}{2}$ ）中，⊙O的“随心点”是；

(2)、若点E（4，3）是⊙O的“随心点”，求⊙O的半径r的取值范围；

(3)、当⊙O的半径r=2时，直线y=- x+b（b≠0）与x轴交于点M，与y轴交于点N，若线段MN上存在⊙O的“随心点”，直接写出b的取值范围．

查看试题解析