北京市门头沟区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-05 类型:期末考试
一、单选题
-
1. 反比例函数 的图象分布的象限是( )A、第一、三象限 B、第二、四象限 C、第一象限 D、第二象限2. ⊙O的半径为3,点P到圆心O的距离为5,点P与⊙O的位置关系是( )A、无法确定 B、点P在⊙O外 C、点P在⊙O上 D、点P在⊙O内3. 将抛物线 y=2x2 的图象先向右平移2个单位,再向上平移3个单位后,得到的抛物线的解析式是( )A、y=2(x-2)2-3 B、 y=2(x-2)2+3 C、2(x+2)2-3 D、 2(x+2)2+34. 如图,△ABC的顶点都在方格纸的格点上,那么 的值为( )
 A、 B、 C、 D、5. 如图是一个正方体纸盒,在下面四个平面图形中,是这个正方体纸盒展开图的是( )
A、 B、 C、 D、5. 如图是一个正方体纸盒,在下面四个平面图形中,是这个正方体纸盒展开图的是( ) A、
A、 B、
B、 C、
C、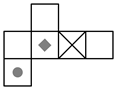 D、
D、 6. 如图,AB是半圆O的直径,半径OC⊥AB于O , AD平分∠CAB交 于点D , 连接CD , OD , BD . 下列结论中正确的是( )
6. 如图,AB是半圆O的直径,半径OC⊥AB于O , AD平分∠CAB交 于点D , 连接CD , OD , BD . 下列结论中正确的是( ) A、AC∥OD B、 C、△ODE∽△ADO D、7. 对于不为零的两个实数a , b , 如果规定a★b ,那么函数 的图象大致是( )A、
A、AC∥OD B、 C、△ODE∽△ADO D、7. 对于不为零的两个实数a , b , 如果规定a★b ,那么函数 的图象大致是( )A、 B、
B、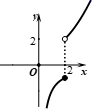 C、
C、 D、
D、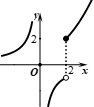 8. 近年来,移动支付已成为主要支付方式之一.为了解某校800名学生上个月A , B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A , B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
8. 近年来,移动支付已成为主要支付方式之一.为了解某校800名学生上个月A , B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A , B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
下面有四个推断:
①从全校学生中随机抽取1人,该学生上个月仅使用A支付的概率为0.3;
②从全校学生中随机抽取1人,该学生上个月A , B两种支付方式都使用的概率为0.45;
③估计全校仅使用B支付的学生人数为200人;
④这100名学生中,上个月仅使用A和仅使用B支付的学生支付金额的中位数为800元.
其中合理推断的序号是( )
A、①② B、①③ C、①④ D、②③二、填空题
-
9. 如果∠A是锐角,且sinA= ,那么∠A=゜.10. 在如图所示的几何体中,其三视图中有三角形的是(填序号).
 11. 如果二次函数 的图象如图所示,那么abc0 .(填“>”,“=”,或“<”).
11. 如果二次函数 的图象如图所示,那么abc0 .(填“>”,“=”,或“<”). 12. 写出一个具有性质“在每个象限内y随x的增大而减小”的反比例函数的表达式为.13. 如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为 .
12. 写出一个具有性质“在每个象限内y随x的增大而减小”的反比例函数的表达式为.13. 如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为 . 14. “永定楼”,作为门头沟区的地标性建筑,因其坐落在永定河畔而得名.为测得其高度,低空无人机在A处,测得楼顶端B的仰角为30°,楼底端C的俯角为45°,此时低空无人机到地面的垂直距离AE为23 米,那么永定楼的高度BC是米(结果保留根号).
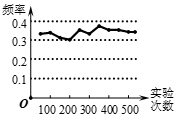
14. “永定楼”,作为门头沟区的地标性建筑,因其坐落在永定河畔而得名.为测得其高度,低空无人机在A处,测得楼顶端B的仰角为30°,楼底端C的俯角为45°,此时低空无人机到地面的垂直距离AE为23 米,那么永定楼的高度BC是米(结果保留根号). 15. 如图是某小组同学做“频率估计概率”的实验时,绘出的某一实验结果出现的频率折线图,则符合图中这一结果的实验可能是(填序号).
15. 如图是某小组同学做“频率估计概率”的实验时,绘出的某一实验结果出现的频率折线图,则符合图中这一结果的实验可能是(填序号).①抛一枚质地均匀的硬币,落地时结果“正面朝上”;
②在“石头,剪刀,布”的游戏中,小明随机出的是剪刀;
③四张一样的卡片,分别标有数字1,2,3,4,从中随机取出一张,数字是1.
 16. 张华在网上经营一家礼品店,春节期间准备推出四套礼品进行促销,其中礼品甲45元/套,礼品乙50元/套,礼品丙70元/套,礼品丁80元/套,如果顾客一次购买礼品的总价达到100元,顾客就少付x元,每笔订单顾客网上支付成功后,张华会得到支付款的80%.
16. 张华在网上经营一家礼品店,春节期间准备推出四套礼品进行促销,其中礼品甲45元/套,礼品乙50元/套,礼品丙70元/套,礼品丁80元/套,如果顾客一次购买礼品的总价达到100元,顾客就少付x元,每笔订单顾客网上支付成功后,张华会得到支付款的80%.①当x=5时,顾客一次购买礼品甲和礼品丁各1套,需要支付元;
②在促销活动中,为保证张华每笔订单得到的金额均不低于促销前总价的六折,则x的最大值为 .
三、解答题
-
17. 计算: .18. 已知二次函数 .
 (1)、用配方法将其化为 的形式;(2)、在所给的平面直角坐标系xOy中,画出它的图象.19. 如图,在平面直角坐标系xOy中,点A( ,3),B( ,2),C(0, ).
(1)、用配方法将其化为 的形式;(2)、在所给的平面直角坐标系xOy中,画出它的图象.19. 如图,在平面直角坐标系xOy中,点A( ,3),B( ,2),C(0, ).
⑴以y轴为对称轴,把△ABC沿y轴翻折,画出翻折后的△ ;
⑵在(1)的基础上,
①以点C为旋转中心,把△ 顺时针旋转90°,画出旋转后的△ ;
②点 的坐标为( ),在旋转过程中点 经过的路径 的长度为( )(结果保留π).
20. 下面是小华同学设计的“作三角形的高线”的尺规作图的过程.
已知:如图1,△ABC .
求作:AB边上的高线.
作法:如图2,
①分别以A , C为圆心,大于 长
为半径作弧,两弧分别交于点D , E;
② 作直线DE , 交AC于点F;
③ 以点F为圆心,FA长为半径作圆,交AB的延长线于点M;
④ 连接CM .
则CM 为所求AB边上的高线.
根据上述作图过程,回答问题:
(1)、用直尺和圆规,补全图2中的图形;(2)、完成下面的证明:证明:连接DA , DC , EA , EC ,
∵由作图可知DA=DC =EA=EC ,
∴DE是线段AC的垂直平分线.
∴FA=FC .
∴AC是⊙F的直径.
∴∠AMC=°()(填依据),
∴CM⊥AB .
即CM就是AB边上的高线.
21. 如图,在四边形ABCD中,AD∥BC , AB⊥BD于点B . 已知∠A = 45°,∠C= 60°, ,求AD的长. 22. 已知二次函数 .(1)、求证:无论m取任何实数时,该函数图象与x轴总有交点;(2)、如果该函数的图象与x轴交点的横坐标均为正数 , 求m的最小整数值.23. 在平面直角坐标系 中,直线 与双曲线 交于点A(2,a).
22. 已知二次函数 .(1)、求证:无论m取任何实数时,该函数图象与x轴总有交点;(2)、如果该函数的图象与x轴交点的横坐标均为正数 , 求m的最小整数值.23. 在平面直角坐标系 中,直线 与双曲线 交于点A(2,a). (1)、求a与k的值;(2)、画出双曲线 的示意图;(3)、设点 是双曲线 上一点(P与A不重合),直线 与y轴交于点 ,当 时,结合图象,直接写出b的值.24. 如图,在Rt△ABC中,∠C = 90°,点O是斜边AB上一定点,到点O的距离等于OB的所有点组成图形W , 图形W与AB , BC分别交于点D , E , 连接AE , DE , ∠AED=∠B .
(1)、求a与k的值;(2)、画出双曲线 的示意图;(3)、设点 是双曲线 上一点(P与A不重合),直线 与y轴交于点 ,当 时,结合图象,直接写出b的值.24. 如图,在Rt△ABC中,∠C = 90°,点O是斜边AB上一定点,到点O的距离等于OB的所有点组成图形W , 图形W与AB , BC分别交于点D , E , 连接AE , DE , ∠AED=∠B . (1)、判断图形W与AE所在直线的公共点个数,并证明.(2)、若 , ,求OB .25. 如图, 是直径AB所对的半圆弧,点C在 上,且∠CAB =30°,D为AB边上的动点(点D与点B不重合),连接CD , 过点D作DE⊥CD交直线AC于点E .
(1)、判断图形W与AE所在直线的公共点个数,并证明.(2)、若 , ,求OB .25. 如图, 是直径AB所对的半圆弧,点C在 上,且∠CAB =30°,D为AB边上的动点(点D与点B不重合),连接CD , 过点D作DE⊥CD交直线AC于点E .
小明根据学习函数的经验,对线段AE , AD长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)、对于点D在AB上的不同位置,画图、测量,得到线段AE , AD长度的几组值,如下表:位置1
位置2
位置3
位置4
位置5
位置6
位置7
位置8
位置9
AE/cm
0.00
0.41
0.77
1.00
1.15
1.00
0.00
1.00
4.04
…
AD/cm
0.00
0.50
1.00
1.41
2.00
2.45
3.00
3.21
3.50
…
在AE , AD的长度这两个量中,确定的长度是自变量,的长度是这个自变量的函数;
(2)、在下面的平面直角坐标系 中,画出(1)中所确定的函数的图象; (3)、结合画出的函数图象,解决问题:当AE= AD时,AD的长度约为cm(结果精确到0.1).26. 在平面直角坐标系 中,抛物线 的顶点为P , 且与y轴交于点A , 与直线 交于点B , C(点B在点C的左侧).
(3)、结合画出的函数图象,解决问题:当AE= AD时,AD的长度约为cm(结果精确到0.1).26. 在平面直角坐标系 中,抛物线 的顶点为P , 且与y轴交于点A , 与直线 交于点B , C(点B在点C的左侧). (1)、求抛物线 的顶点P的坐标(用含a的代数式表示);(2)、横、纵坐标都是整数的点叫做整点,记抛物线与线段AC围成的封闭区域(不含边界)为“W区域”.
(1)、求抛物线 的顶点P的坐标(用含a的代数式表示);(2)、横、纵坐标都是整数的点叫做整点,记抛物线与线段AC围成的封闭区域(不含边界)为“W区域”.①当 时,请直接写出“W区域”内的整点个数;
②当“W区域”内恰有2个整点时,结合函数图象,直接写出a的取值范围.
27. 如图,∠MON=60°,OF平分∠MON , 点A在射线OM上, P , Q是射线ON上的两动点,点P在点Q的左侧,且PQ=OA , 作线段OQ的垂直平分线,分别交OM , OF , ON于点D , B , C , 连接AB , PB .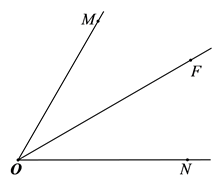
 (1)、依题意补全图形;(2)、判断线段 AB , PB之间的数量关系,并证明;(3)、连接AP , 设 ,当P和Q两点都在射线ON上移动时, 是否存在最小值?若存在,请直接写出 的最小值;若不存在,请说明理由.28. 对于平面直角坐标系 中的图形M , N , 给出如下定义:如果点P为图形M上任意一点,点Q为图形N上任意一点,那么称线段PQ长度的最小值为图形M , N的“近距离”,记作 d(M , N).若图形M , N的“近距离”小于或等于1,则称图形M , N互为“可及图形”.
(1)、依题意补全图形;(2)、判断线段 AB , PB之间的数量关系,并证明;(3)、连接AP , 设 ,当P和Q两点都在射线ON上移动时, 是否存在最小值?若存在,请直接写出 的最小值;若不存在,请说明理由.28. 对于平面直角坐标系 中的图形M , N , 给出如下定义:如果点P为图形M上任意一点,点Q为图形N上任意一点,那么称线段PQ长度的最小值为图形M , N的“近距离”,记作 d(M , N).若图形M , N的“近距离”小于或等于1,则称图形M , N互为“可及图形”.
 (1)、当⊙O的半径为2时,如果点A(0,1),B(3,4),那么d(A , ⊙O)= , d(B , ⊙O)= ;(2)、当⊙O的半径为2时,如果直线 与⊙O互为“可及图形”,求b的取值范围;(3)、⊙G的圆心G在x轴上,半径为1,直线 与x轴交于点C , 与y轴交于点D , 如果⊙G和∠CDO互为“可及图形”,直接写出圆心G的横坐标m的取值范围.
(1)、当⊙O的半径为2时,如果点A(0,1),B(3,4),那么d(A , ⊙O)= , d(B , ⊙O)= ;(2)、当⊙O的半径为2时,如果直线 与⊙O互为“可及图形”,求b的取值范围;(3)、⊙G的圆心G在x轴上,半径为1,直线 与x轴交于点C , 与y轴交于点D , 如果⊙G和∠CDO互为“可及图形”,直接写出圆心G的横坐标m的取值范围.