安徽省芜湖市无为县2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列垃圾分类的图标（不含文字与字母部分）中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列长度的三条线段中，能围成三角形的是（）

A、5cm ， 6cm ， 12cm B、3cm ， 4cm ， 5cm C、4cm ， 6cm ， 10cm D、3cm ， 4cm ， 8cm

查看试题解析
3. 下列运算正确的是（）

A、x²+x²＝2x⁴ B、（x+3y）（x﹣3y）＝x²﹣3y² C、a^﹣²•a³＝a D、（﹣2x²）⁴＝16x⁶

查看试题解析
4. 如图，AC与BD相交于点O ， ∠DAB＝∠CBA ，添加下列哪一个条件后，仍不能使△ADB≌△CBA的是（）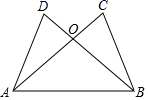

A、AD＝BC B、∠ABD＝∠BAC C、OA＝OB D、AC＝BD

查看试题解析
5. 分式 $\frac{a^{2} - 1}{a^{2} - 2 a + 1}$ 的值等于0，则a的值为（）

A、±1 B、1 C、﹣1 D、2

查看试题解析
6. 经过我省的合福高铁被称为“最美高铁”，从合肥途径无为至福州全程848km的路段，乘坐相谱号高速列车比乘坐普通列车全程直达所用时间缩短了5h ，已知高铁的平均时速是普通列车平均时速的2.5倍，若设普通列车的平均时速为xkm/h ．则根据题意可列方程为（）

A、 $\frac{848}{x} - \frac{848}{x - 5} = 2.5$ B、 $\frac{848}{x} - \frac{848}{2.5 x} = 5$ C、 $\frac{848}{x - 5} - \frac{848}{x} = 2.5$ D、 $\frac{848}{2.5 x} - \frac{848}{x} = 5$

查看试题解析
7. 如图，将图1中阴影部分拼成图2，根据两个图形中阴影部分的关系，可以验证下列哪个计算公式（）

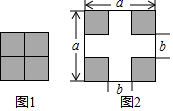A、（a﹣b）²＝a²﹣2ab+b² B、（a+b）²＝a²+2ab+b² C、（a﹣b）²＝（a+b）²﹣4ab D、（a+b）（a﹣b）＝a²﹣b²

查看试题解析
8. 在4×4的正方形网格中，以格点为顶点的三角形称为格点三角形，在图中画出与△ABC关于某条直线对称的格点三角形，最多能画（）个．

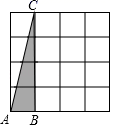A、5 B、6 C、7 D、8

查看试题解析
9. 如图，在△ABC中，∠BAC的平分线AD和边BC的垂直平分线ED相交于点D ，过点D作DF垂直于AC交AC的延长线于点F ，若AB＝8，AC＝5，则CF＝（）

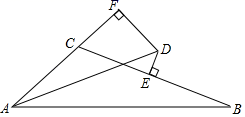A、1.5 B、2 C、2.5 D、3

查看试题解析
10. 若x≠1，则我们把﹣ $\frac{1}{x + 1}$ 称为x的“和1负倒数”，如：2的“和1负倒数”为﹣ $\frac{1}{3}$ ，﹣3的“和1负倒数”为 $\frac{1}{2}$ ．若x₁＝ $\frac{2}{3}$ ，x₂是x₁的“和1负倒数”，x₃是x₂的“和1负倒数”，…，依此类推，则x₂₀₁₉的值为（）

A、 $\frac{2}{3}$ B、﹣ $\frac{3}{5}$ C、 $\frac{7}{5}$ D、﹣ $\frac{5}{2}$

查看试题解析

二、填空题

11. 纳米（nm）是非常小的长度单位，1nm＝10^﹣⁹m ．某种猪瘟病毒的直径为120nm ， “120nm”用科学记数法表示为m ．

查看试题解析
12. 已知点A（a+2，5）与点B（5，b）关于x轴对称，则a﹣b＝．

查看试题解析
13. 因式分解：2x³y﹣8xy＝．

查看试题解析
14. 如图，在一张直角三角形纸片ABC中，∠ACB＝90°，∠A＝30°P是边AB上的一动点，将△ACP沿着CP折叠至△A₁CP ，当△A₁CP与△ABC的重叠部分为等腰三角形时，则∠ACP的度数为．

查看试题解析

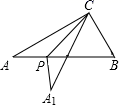
三、解答题

15. 计算：（﹣2x）²﹣（2x+1）（2x﹣1）+（x﹣2）²

查看试题解析
16. 解分式方程： $\frac{3}{x^{2} + x} - \frac{1}{x^{2} - x} = 0$ ．

查看试题解析
17. 先化简，再求值： $\frac{a^{2} - b^{2}}{a^{2} + a b}$ ÷（a﹣ $\frac{2 a b - b^{2}}{a}$ ），其中a＝3，b＝1．

查看试题解析
18. 阅读材料：人教版八年级上册数学教材第121页的“阅读与思考”内容介绍，在因式分解中有一类形如x²+（p+q）x+pq的多项式，其常数项是两个因数的积，而一次项系数恰好是这两个因数的和，则我们可以把它分解成x²+（p+q）x+pq＝（x+p）（x+q）．
例如，x²+3x+2＝x²+（1+2）x+1×2＝（x+1）（x+2），具体做法是先分解二次项系数，分别写在十字交叉线的左上角和左下角，再分解常数项，分别写在十字交叉线的右上角和右下角：然后交叉相乘，求代数和，使其等于一次项系数（如图），这种方法称为“十字相乘法”．

解决问题：

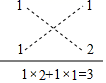(1)、请模仿上例，运用十字相乘法将多项式x²﹣x﹣6因式分解（画出十字相乘图）

(2)、若多项式x²+kx﹣12可以分解成（x+m）（x+n）（m ， n为整数）的形式，则m+n的最大值为．

查看试题解析
19. 如图，在平面直角坐标系中有一个△ABC，顶点A（﹣1，3），B（2，0），C（﹣3，﹣1）．

(1)、画出△ABC关于y轴的对称轴图形△A₁B₁C₁（不写画法）；
点A₁的坐标为；点B₁的坐标为；点C₁的坐标为．

(2)、若网格上的每个小正方形的边长为1，则△ABC的面积是．

查看试题解析
20. 如图，已知∠AOB ，以O为圆心，以任意长为半径作弧，分别交OA ， OB于F ， E两点，再分别以E ， F为圆心，大于 $\frac{1}{2}$ EF长为半径作圆弧，两条圆弧交于点P ，作射线OP ，过点F作FD∥OB交OP于点D.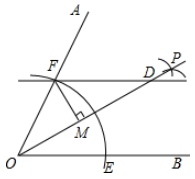

(1)、若∠OFD＝116°，求∠DOB的度数；

(2)、若FM⊥OD ，垂足为M ，求证：△FMO≌△FMD.

查看试题解析
21. 为了响应习近平总书记“绿水青山就是金山银山”的号召，芜湖市对境内24km长江干流岸线环境进行集中专项整治，全部工程由甲乙两家施工队共同分别从上、下游同时进行，已知乙施工队的平均整治速度是甲施工队的1.5倍，原计划用若干天完成，后来为了提前完工，两家施工队都将施工速度提高20%，结果比原计划提前两天完成全部整治任务，求甲施工队原计划平均每天整治多少m？

查看试题解析
22. 已知a ， b是实数，定义关于“△”的一种运算如下：a△b＝（a﹣b）²﹣（a+b）² ．

(1)、小明通过计算发现a△b＝﹣4ab ，请说明它成立的理由．

(2)、利用以上信息得x $Δ \frac{1}{x}$ ＝，若x $+ \frac{1}{x}$ ＝3，求（x $- \frac{1}{x}$ ）⁴的值．

(3)、请判断等式（a△b）△c＝a△（b△c）是否成立？并说明理由．

查看试题解析
23. 学习与探究：
在等边△ABC中，P是射线AB上的一点．

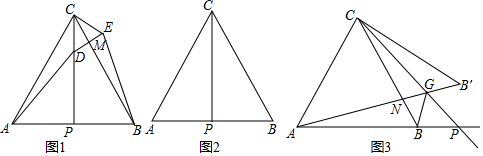(1)、探索实践：
如图1，P是边AB的中点，D是线段CP上的一个动点，以CD为边向右侧作等边△CDE ， DE与BC交于点M ，连结BE ．

①求证：AD＝BE；

②连结BD ，当DB+DM最小时，试在图2中确定D的位置，并说明理由；（要求用尺规作图，保留作图痕迹）

③在②的条件下，求△CME与△ACM的面积之比．

(2)、思维拓展：
如图3，点P在边AB的延长线上，连接CP ，点B关于直线CP的对称点为B'，连结AB'，CB'，AB'交BC于点N ，交直线CP于点G ，连结BG ．请判断∠AGC与∠AGB的大小关系，并证明你的结论．

查看试题解析