安徽省芜湖市2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-05 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,下列各点位于第三象限的是( )A、 B、 C、 D、2. 下列交通警示标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 在平面直角坐标系中,将点 向下平移2个单位长度后的坐标是( )A、 B、 C、 D、4. 下列命题是真命题的是( )A、同位角相等 B、三角形的两个锐角互余 C、对顶角相等 D、若 ,则5. 若线段AP,AQ分别是△ABC边上的高线和中线,则( )A、AP>AQ B、AP≥AQ C、AP<AQ D、AP≤AQ6. 如图,在 和 中, , .若添加条件后使得 ,则在下列条件中,添加错误的是( )
3. 在平面直角坐标系中,将点 向下平移2个单位长度后的坐标是( )A、 B、 C、 D、4. 下列命题是真命题的是( )A、同位角相等 B、三角形的两个锐角互余 C、对顶角相等 D、若 ,则5. 若线段AP,AQ分别是△ABC边上的高线和中线,则( )A、AP>AQ B、AP≥AQ C、AP<AQ D、AP≤AQ6. 如图,在 和 中, , .若添加条件后使得 ,则在下列条件中,添加错误的是( )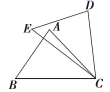 A、 B、 C、 D、7. 若一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=0的解为( )
A、 B、 C、 D、7. 若一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=0的解为( ) A、x=﹣2 B、x=﹣0.5 C、x=﹣3 D、x=﹣48. 如图, ,若 , ,则 的度数为( )
A、x=﹣2 B、x=﹣0.5 C、x=﹣3 D、x=﹣48. 如图, ,若 , ,则 的度数为( ) A、 B、 C、 D、9. 若直线 与直线 的交点在第四象限,则 的取值范围是( )A、 B、 C、 D、 或10. 如图, 是 的角平分线,点 是 上一点,作线段 的垂直平分线交 于点 ,交 于点 ,过点 作 交 于点 ,连接 ,若 , .则 的面积为( )
A、 B、 C、 D、9. 若直线 与直线 的交点在第四象限,则 的取值范围是( )A、 B、 C、 D、 或10. 如图, 是 的角平分线,点 是 上一点,作线段 的垂直平分线交 于点 ,交 于点 ,过点 作 交 于点 ,连接 ,若 , .则 的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若正比例函数 的图象经过第一、三象限,则 的取值范围是 .12. 如图,△ABC被撕去了一角,经测量得∠A=68°,∠B=23°,则△ABC是三角形.(填“锐角”“直角”或“钝角”)
 13. 如图,在 中, , , ,则 的面积为 .
13. 如图,在 中, , , ,则 的面积为 . 14. 如图,在 中, 厘米, 厘米,点 为 的中点.如果点 在线段 上以3厘米/秒的速度由 点向 点运动,同时,点 在线段 上,由 点向 点运动,当点 的运动速度为厘米/秒时,能够使 与 全等.
14. 如图,在 中, 厘米, 厘米,点 为 的中点.如果点 在线段 上以3厘米/秒的速度由 点向 点运动,同时,点 在线段 上,由 点向 点运动,当点 的运动速度为厘米/秒时,能够使 与 全等.
三、解答题
-
15. 如图,直线 与直线 相交于点 .
 (1)、求 的值和直线 的函数解析式.(2)、当 时, 的取值范围是 .16. 如图,在平面直角坐标系中, 的顶点都在网格点上,按下列要求画图.
(1)、求 的值和直线 的函数解析式.(2)、当 时, 的取值范围是 .16. 如图,在平面直角坐标系中, 的顶点都在网格点上,按下列要求画图. (1)、画出 关于 轴对称的 .(2)、将 向上平移3个单位长度得到 .17. 如图,在△ABC中,∠CAE=20°,∠C=40°,∠CBD=30°,求∠AFB的度数。
(1)、画出 关于 轴对称的 .(2)、将 向上平移3个单位长度得到 .17. 如图,在△ABC中,∠CAE=20°,∠C=40°,∠CBD=30°,求∠AFB的度数。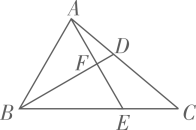 18. 如图,在平面直角坐标系 中,点 均在坐标轴上, , 平分 交 轴于点 , 平分 交 轴于点 ,求 的值.
18. 如图,在平面直角坐标系 中,点 均在坐标轴上, , 平分 交 轴于点 , 平分 交 轴于点 ,求 的值. 19. 如图,在 中, 是边 上一点, ,作 交 的延长线于点 .
19. 如图,在 中, 是边 上一点, ,作 交 的延长线于点 . (1)、证明: .(2)、若 , , ,求 .20. 在 中, , .
(1)、证明: .(2)、若 , , ,求 .20. 在 中, , . (1)、如图1,已知线段 的垂直平分线与 边交于点 ,连接 ,求 的度数.(2)、如图2,若点 是 上一点,且 ,连接 .求证: .21. 如图,点 在三角形 的边 上,且 .
(1)、如图1,已知线段 的垂直平分线与 边交于点 ,连接 ,求 的度数.(2)、如图2,若点 是 上一点,且 ,连接 .求证: .21. 如图,点 在三角形 的边 上,且 . (1)、求证: .(2)、若 的平分线 交 于点 , 交 于点 ,求证: .
(1)、求证: .(2)、若 的平分线 交 于点 , 交 于点 ,求证: .

