安徽省六安市裕安区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在平面直角坐标系中，点 $M (- 3, - 6)$ 关于 $y$ 轴对称的点的坐标为（）

A、 $(- 3, 6)$ B、 $(3, - 6)$ C、 $(3, 6)$ D、 $(- 6, - 3)$

查看试题解析
3. 下列命题与其逆命题都是真命题的是（）

A、全等三角形对应角相等 B、对顶角相等 C、角平分线上的点到角的两边的距离相等 D、若a²>b²,则a>b

查看试题解析
4. 若一次函数y=(k-3)x-1的图像不经过第一象限，则（）

A、k<3 B、k>3 C、k>0 D、k<0

查看试题解析
5. 如图，点A，D，C，F在一条直线上，AB=DE，∠A=∠EDF，下列条件不能判定△ABC≌△DEF的是（）

A、AD=CF B、∠BCA=∠F C、∠B=∠E D、BC=EF

查看试题解析
6. 如图，工人师傅做了一个长方形窗框ABCD ， E ， F ， G ， H分别是四条边上的中点，为了稳固，需要在窗框上钉一根木条，这根木条不应钉在（）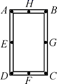

A、G ， H两点处 B、A ， C两点处 C、E ， G两点处 D、B ， F两点处

查看试题解析
7. 一次函数 $y = k x + b (k \neq 0)$ 的图象如图所示 $y < 0$ 的取值范围是（）

A、 $x < 3$ B、 $x > 0$ C、 $x < 2$ D、 $x > 2$

查看试题解析
8. 如下图，点 $E$ 是 $B C$ 的中点， $A B ⊥ B C$ ， $D C ⊥ B C$ ， $A E$ 平分 $∠ B A D$ ，下列结论：
① $∠ A E D = 90^{\circ}$ ② $∠ A D E = ∠ C D E$ ③ $D E = B E$ ④ $A D = A B + C D$

四个结论中成立的是（）

A、①②④ B、①②③ C、②③④ D、①③④

查看试题解析
9.
如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是（　　）

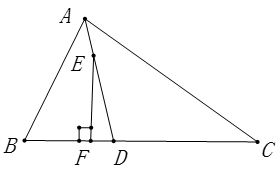
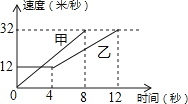A、乙前4秒行驶的路程为48米 B、在0到8秒内甲的速度每秒增加4米/秒 C、两车到第3秒时行驶的路程相等 D、在4至8秒内甲的速度都大于乙的速度

查看试题解析
10. 如图，在△ABC中，∠BAC=60°，∠BAC的平分线AD与边BC的垂直平分线相交于点D，DE⊥AB交AB的延长线于点E，DF⊥AC于点F，现有下列结论：①DE=DF；②DE+DF=AD；③AM平分∠ADF；④AB+AC=2AE；其中正确的有（）

A、2个 B、3个 C、4个 D、1个

查看试题解析

二、填空题

11. 若△ABC的三边的长AB＝5，BC＝2a+1，AC＝3a﹣1，则a的取值范围为．

查看试题解析
12. 如图，在 $Δ A B C$ 中. $A D$ 是 $∠ B A C$ 的平分线. $E$ 为 $A D$ 上一点， $E F ⊥ B C$ 于点 $F$ .若 $∠ C = 35^{\circ}$ ， $∠ D E F = 15^{\circ}$ ，则 $∠ B$ 的度数为．

查看试题解析
13. 如图，在平面直角坐标系中， $O$ 为坐标原点，点 $A (0 ， 3)$ 和点 $B (2 ， 0)$ 是坐标轴上两点，点 $C (m ， n) (m \neq n)$ 为坐标轴上一点，若三角形 $A B C$ 的面积为 $3$ ，则 $C$ 点坐标为.

查看试题解析
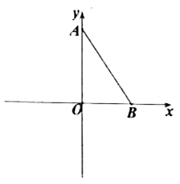14. 如图，在平面直角坐标系中，已如点A（1，1），B（-1，1），C（-1，-2），D（1，-2），把一根长为2019个单位长度没有弹性的细线(线的相细忽略不计)的一端固定在A处，并按 $A \to B \to C \to D \to A$ 的规律紧绕在四边形ABCD的边上，则细线的另一端所在位置的点的坐标是.

查看试题解析

三、解答题

15. 如图， $Δ A C F ≅ Δ A D E ， A D = 12 ， A E = 5$ ，求 $D F$ 的长，

查看试题解析
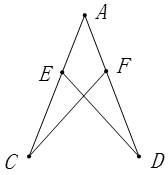16. 已知一次函数 $y = k x + b$ 的图象经过点 $(- 2, 5)$ ，并且与 $y$ 轴相交于点 $P$ ，直线 $y = - x + 3$ 与 $y$ 轴相交于点 $Q$ ，点 $Q$ 恰与点 $P$ 关于 $x$ 轴对称，求这个一次函数 $y = k x + b$ 的表达式．

查看试题解析
17. 如图，在△ABC中，∠BAC是钝角，按要求完成下列画图．（不写作法，保留作图痕迹）

⑴用尺规作∠BAC的平分线AE和AB边上的垂直平分线MN；

⑵用三角板作AC边上的高BD ．

查看试题解析
18. 如图，已知在 $Δ A B C$ 和 $Δ A E F$ 中， $A B = A C ， A E = A F ， ∠ C A B = ∠ E A F . B E$ 交 $F C$ 于 $O$ 点，

(1)、求证： $B E = C F$ ；

(2)、当 $∠ B A C = 70^{\circ}$ 时，求 $∠ B O C$ 的度数．

查看试题解析
19. 已知：如图，把 $Δ A B C$ 向上平移 $3$ 个单位长度，再向右平移 $2$ 个单位长度，得到 $Δ A' B' C'$ ；

(1)、写出 $A' ， B' ， C'$ 的坐标；

(2)、求出 $Δ A B C$ 的面积；

(3)、点 $P$ 在 $y$ 轴上，且 $Δ B C P$ 与 $Δ A B C$ 的面积相等，求点 $P$ 的坐标．

查看试题解析
20. 如图，在△ABC中，∠BAC=90°，∠B=50°，AE，CF是角平分线，它们相交于为O，AD是高，求∠BAD和∠AOC的度数.

查看试题解析

21. 小明平时喜欢玩“开心消消乐”游戏，本学期在学校组织的几次数学反馈性测试中，小明的数学成绩如下表：

月份 $x$	$9$	$10$	$11$	$12$	$13$ （第二年元月）	$14$ （第二年2月）
成绩（分）	$90$	$80$	$70$	$60$	···	···

(1)、以月份为x轴，成绩为y轴，根据上表提供的数据在平面直角坐标系中描点；

(2)、观察（1）中所描点的位置关系，猜想

y

与

x

之间的的函数关系，并求出所猜想的函数表达式；

(3)、若小明继续沉溺于“开心消消乐“游戏，照这样的发展趋势，请你估计元月（此时

x = 13

）份的考试中小明的数学成绩，并用一句话对小明提出一些建议．

查看试题解析

22. 如图，在△ABC中，AB=AC ， ∠BAC=90°，点P是BC上的一动点，AP=AQ ， ∠PAQ=90°，连接CQ ．

(1)、求证：CQ⊥BC ．

(2)、△ACQ能否是直角三角形？若能，请直接写出此时点P的位置；若不能，请说明理由.

(3)、当点P在BC上什么位置时，△ACQ是等腰三角形？请说明理由．

查看试题解析
23. 在购买某场足球赛门票时，设购买门票数为x（张），总费用为y（元）.现有两种购买方案：
方案一：若单位赞助广告费10000元，则该单位所购门票的价格为每张60元；

（总费用＝广告赞助费+门票费）

方案二：购买门票方式如图所示.

解答下列问题：

(1)、方案一中，y与x的函数关系式为；
方案二中，当0≤x≤100时，y与x的函数关系式为，当x＞100时，y与x的函数关系式为；

(2)、如果购买本场足球赛门票超过100张，你将选择哪一种方案，使总费用最省？请说明理由；

(3)、甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张，花去总费用计58000元，求甲、乙两单位各购买门票多少张.

查看试题解析