安徽省淮北市濉溪县2019-2020学年八年级上学期数学期末试卷
试卷更新日期：2020-11-05 类型：期末考试
一、单选题
-
1. 函数y= 中，自变量x的取值范围是（ ）A、x≥0 B、x＞0 C、x≠3 D、.x≥-32. 在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中.轴对称图形是（ ）A、
B、
C、
D、
3. 若点A（a+1，b﹣2）在第二象限，则点B（﹣a，b+1）在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 已知△ABC中，∠B是∠A的2倍，∠C比∠A大20°，则∠A等于( )A、40° B、60° C、80° D、90°5. 如图，已知∠ABC=∠DCB，下列所给条件不能证明△ABC≌△DCB的是（ ）
A、∠A=∠D B、AB=DC C、∠ACB=∠DBC D、AC=BD6. 如图，在△ABC中，DE是AC的垂直平分线，且分别交BC，AC于点D和E，∠B＝60°，∠C＝25°，则∠BAD为（ ）
A、50° B、70° C、75° D、80°7. 关于x的一次函数y=(2m-10)x+2m-8的图象不经过第三象限，m的取值范围是（ ）A、m＜5 B、m＞4 C、4≤m＜5 D、4＜m＜58. 下列命题：①形状相同的两个三角形是全等形；②在两个三角形中，相等的角是对应角，相等的边是对应边；③全等三角形对应边上的高、中线及对应角平分线分别相等；④到已知角两边距离相等的点都在同一条直线上.其中真命题有（ ）A、1个 B、2个 C、3个 D、4个9. 如图，已知等边△ABC的周长是12，点P是三角形内的任意一点，PD∥AB，PE∥BC，PF∥AC则PD+PE+PF的值是（ ）
A、12 B、8 C、4 D、310. 如图，在△ABC中，AD为∠BAC的平分线，BM⊥AD，垂足为M，且AB=5，BM=2，AC=9，则∠ABC与∠C的关系为（ ）
A、∠ABC=2∠C B、∠ABC= ∠C C、 ∠ABC=∠C D、∠ABC=3∠C二、填空题
-
11. 一次函数y＝(2m－6)x＋5中，y随x的增大而减小，则m的取值范围是 ．12. 如图，在Rt△ABC中，∠C=90°，∠A=30°，∠ABC的平分线BD交AC于点D．若BD=10cm，则点D到AB的距离是.
13. 当m=时，直线y=-2x+m与直线y=4x-2的交点在x轴上.14. 如图，在△ABC中，BI，CI分别平分∠ABC，∠ACF，直线DE过点I，且DE∥BC，BD＝8 cm，CE＝5 cm，则DE＝ ．
15. 如图，在等腰△ABC中，AB＝AC，∠BAC＝50°．∠BAC的平分线与AB的中垂线交于点O，点C沿EF折叠后与点O重合，则∠CEF的度数是 ．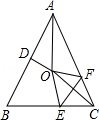
三、解答题
-
16. 在如图，所示的平面直角坐标系中，作出下列坐标的A(-3，2)，B(0，-4)，C(5，-3)， D(0，1).并求出四边形ABCD的面积.
17. 已知y是x的一次函数，它的图象上有两点分别为点A(1，1)，B(5，9).(1)、求这个一次函数的表达式；(2)、判断点C(3，7)是否在这条直线上；(3)、当x取何值时，y＞0？18. 如图，已知AD是△ABC的中线，分别过点B、C作BE⊥AD于点E，CF⊥AD交AD的延长线于点F，求证：BE=CF．
19. 如图，在 中， ，CD平分 交AB于点D， 于点E， 交CD于点F．
求证： ．
20. 某商店以40元/千克的单价新进一批茶叶，经调查发现，在一段时间内，销售量y (千克)与销售单价x (元/千克)之间的函数关系如图所示.
(1)、根据图象，求y与x的函数表达式；(2)、当销售单价为80元/千克时，商店的利润是多少？
