安徽省合肥市瑶海区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-05 类型:期末考试
一、单选题
-
1. 下列图形是轴对称图形的是( )A、
 B、
B、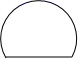 C、
C、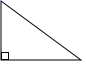 D、
D、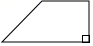 2. 点P(-3,2)到x轴的距离为( )A、-3 B、-2 C、3 D、23. 对于一次函数y=x+2,下列结论错误的是( )A、函数值随自变量增大而增大 B、函数图象与x轴交点坐标是(0,2) C、函数图象与x轴正方向成45°角 D、函数图象不经过第四象限4. 如图,在△ABC和△DEB中,点C在BD边上,AC与BE交于F,若AB=DE,BC=EB,AC=DB,则∠ACB等于( )
2. 点P(-3,2)到x轴的距离为( )A、-3 B、-2 C、3 D、23. 对于一次函数y=x+2,下列结论错误的是( )A、函数值随自变量增大而增大 B、函数图象与x轴交点坐标是(0,2) C、函数图象与x轴正方向成45°角 D、函数图象不经过第四象限4. 如图,在△ABC和△DEB中,点C在BD边上,AC与BE交于F,若AB=DE,BC=EB,AC=DB,则∠ACB等于( )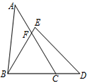 A、∠D B、∠E C、2∠ABF D、 ∠AFB5. 如图所示的钢架中,∠A=18°,焊上等长的钢条P1P2 , P2P3 , P3P4 , P4P5…来加固钢架.∠P5P4B的度数是( )
A、∠D B、∠E C、2∠ABF D、 ∠AFB5. 如图所示的钢架中,∠A=18°,焊上等长的钢条P1P2 , P2P3 , P3P4 , P4P5…来加固钢架.∠P5P4B的度数是( )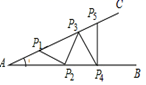 A、80° B、85° C、90° D、100°6. 利用函数 的图象解得 的解集是 ,则 的图象是( )A、
A、80° B、85° C、90° D、100°6. 利用函数 的图象解得 的解集是 ,则 的图象是( )A、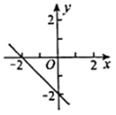 B、
B、 C、
C、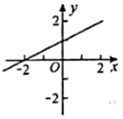 D、
D、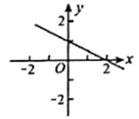 7. 如图,△ABC中,DE垂直平分AC,交AC于E,交BC于D,连接AD,AE=4cm,则△ABC的周长与△ABD的周长差为( )
7. 如图,△ABC中,DE垂直平分AC,交AC于E,交BC于D,连接AD,AE=4cm,则△ABC的周长与△ABD的周长差为( )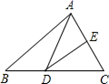 A、2cm B、4cm C、6cm D、8cm8. 已知函数y=kx+b的图象如图,则y=2kx+b的图象可能是( )
A、2cm B、4cm C、6cm D、8cm8. 已知函数y=kx+b的图象如图,则y=2kx+b的图象可能是( )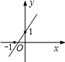 A、
A、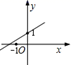 B、
B、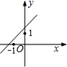 C、
C、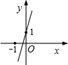 D、
D、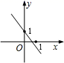 9. 如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE,AE交BC于点D,CD=2,P为AB上一动点,则PD的最小值为( )
9. 如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE,AE交BC于点D,CD=2,P为AB上一动点,则PD的最小值为( )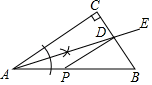 A、2 B、3 C、4 D、无法确定10. 如图,在△ABC中,点D、E在BC边上,点F在AC边上,将△ABD沿着AD翻折,使点B和点E重合,将△CEF沿着EF翻折,点C恰与点A重合.结论:①∠BAC=90°,②DE=EF,③∠B=2∠C,④AB=EC,正确的有( )
A、2 B、3 C、4 D、无法确定10. 如图,在△ABC中,点D、E在BC边上,点F在AC边上,将△ABD沿着AD翻折,使点B和点E重合,将△CEF沿着EF翻折,点C恰与点A重合.结论:①∠BAC=90°,②DE=EF,③∠B=2∠C,④AB=EC,正确的有( )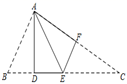 A、①②③④ B、③④ C、①②④ D、①②③
A、①②③④ B、③④ C、①②④ D、①②③二、填空题
-
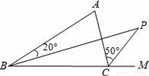
11. 函数y= 中自变量x的取值范围是.12. 如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P=°.
 13. 如图,在△ABC中,AB=AC , ∠A=120°,AB的垂直平分线交BC于M , 交AB于E , AC的垂直平分线交BC于N , 交AC于F , 若MN=2,则NF=
13. 如图,在△ABC中,AB=AC , ∠A=120°,AB的垂直平分线交BC于M , 交AB于E , AC的垂直平分线交BC于N , 交AC于F , 若MN=2,则NF=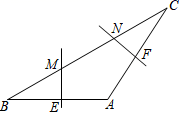 14. 一次函数y=(2a-3)x+a+2(a为常数)的图像,在-1≤x≤1的一段都在x轴上方,则a的取值范围是
14. 一次函数y=(2a-3)x+a+2(a为常数)的图像,在-1≤x≤1的一段都在x轴上方,则a的取值范围是三、解答题
-
15. 已知点 ,解答下列各题:(1)、若点 在 轴上,试求出点 的坐标;(2)、若 ,且 轴,试求出点 的坐标.16. 如图,已知△ABC.
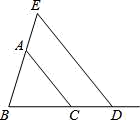 (1)、若AB=4,AC=5,则BC边的取值范围是;(2)、点D为BC延长线上一点,过点D作DE∥AC,交BA的延长线于点E,若∠E=55°,∠ACD=125°,求∠B的度数.17. 如图,△ABC中,AB=AC , D为BC边的中点,DE⊥AB .
(1)、若AB=4,AC=5,则BC边的取值范围是;(2)、点D为BC延长线上一点,过点D作DE∥AC,交BA的延长线于点E,若∠E=55°,∠ACD=125°,求∠B的度数.17. 如图,△ABC中,AB=AC , D为BC边的中点,DE⊥AB .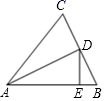 (1)、求证:∠BAC=2∠EDB;(2)、若AC=6,DE=2,求△ABC的面积.18.(1)、已知 ,用直尺和圆规作点 ,使点 到 三边距离相等(不写作法,保留作图痕迹).
(1)、求证:∠BAC=2∠EDB;(2)、若AC=6,DE=2,求△ABC的面积.18.(1)、已知 ,用直尺和圆规作点 ,使点 到 三边距离相等(不写作法,保留作图痕迹).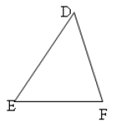 (2)、在图示的网格中,作出 关于 对称的图形 ;说明 是由 经过怎样的平移得到的?
(2)、在图示的网格中,作出 关于 对称的图形 ;说明 是由 经过怎样的平移得到的?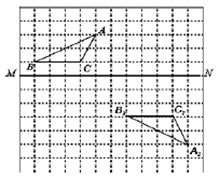 19. 如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.
19. 如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.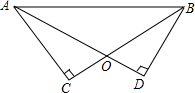 (1)、求证:△ACB≌△BDA;(2)、若∠ABC=36°,求∠CAO度数.20. 如图
(1)、求证:△ACB≌△BDA;(2)、若∠ABC=36°,求∠CAO度数.20. 如图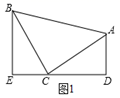
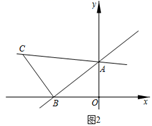 (1)、(模型建立)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED与D,过B作BE⊥ED于E,求证:△BEC≌△CDA;(2)、(模型应用):已知直线 与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;21. 如图,直线y=kx+6与x轴、y轴分别相交于点E、F,点E的坐标为(-8,0),点A的坐标为(-6,0),点P是直线EF上的一个动点.
(1)、(模型建立)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED与D,过B作BE⊥ED于E,求证:△BEC≌△CDA;(2)、(模型应用):已知直线 与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;21. 如图,直线y=kx+6与x轴、y轴分别相交于点E、F,点E的坐标为(-8,0),点A的坐标为(-6,0),点P是直线EF上的一个动点.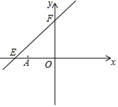 (1)、求k的值;(2)、点P在第二象限内的直线EF上的运动过程中,写出△OPA的面积S与x的函整表达式,并写出自变量x的取值范围;(3)、探究,当点P在直线EF上运动到时,△OPA的面积可能是15吗,若能,请求出点P的坐标;若不能,说明理由.22. 如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)、求k的值;(2)、点P在第二象限内的直线EF上的运动过程中,写出△OPA的面积S与x的函整表达式,并写出自变量x的取值范围;(3)、探究,当点P在直线EF上运动到时,△OPA的面积可能是15吗,若能,请求出点P的坐标;若不能,说明理由.22. 如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.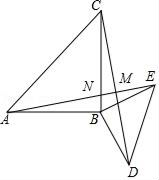 (1)、求证:AE=CD;(2)、求证:AE⊥CD;(3)、连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有(请写序号,少选、错选均不得分).23. 某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.(1)、请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值:
(1)、求证:AE=CD;(2)、求证:AE⊥CD;(3)、连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有(请写序号,少选、错选均不得分).23. 某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.(1)、请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值:C
D
总计/t
A
200
B
x
300
总计/t
240
260
500
(2)、设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求总运费最小的调运方案;(3)、经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.