安徽省合肥市蜀山区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-05 类型:期末考试
一、单选题
-
1. 平面直角坐标系中,点 所在象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列四个图案中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一次函数 的图象上有两点 ,则 与 的大小关系是( )A、 B、 C、 D、无法确定4. 下列命题中,一定是真命题的是( )A、同位角相等 B、三角形中任何两边的和大于第三边 C、三角分别相等的两个三角形全等 D、直线 向下平移2个单位可得到一次函数 的图象5. 如图, ,现添加以下哪个条件不能判定 的是( )
3. 一次函数 的图象上有两点 ,则 与 的大小关系是( )A、 B、 C、 D、无法确定4. 下列命题中,一定是真命题的是( )A、同位角相等 B、三角形中任何两边的和大于第三边 C、三角分别相等的两个三角形全等 D、直线 向下平移2个单位可得到一次函数 的图象5. 如图, ,现添加以下哪个条件不能判定 的是( ) A、 B、 C、 D、6. 等腰三角形中,两条边的长分别是 , ,则三角形的周长是( )A、 B、 C、 或 D、 和7. 如图, 是 延长线上一点, 交 于点 , , ,若 ,则 的长是( )
A、 B、 C、 D、6. 等腰三角形中,两条边的长分别是 , ,则三角形的周长是( )A、 B、 C、 或 D、 和7. 如图, 是 延长线上一点, 交 于点 , , ,若 ,则 的长是( ) A、0.5 B、1 C、1.5 D、28. 如图, ,点 在边 上, ,则 的度数是( )
A、0.5 B、1 C、1.5 D、28. 如图, ,点 在边 上, ,则 的度数是( ) A、25° B、30° C、40° D、75°9. 如图,一次函数 与 的图象相交于点 ,则函数 的图象可能是( )
A、25° B、30° C、40° D、75°9. 如图,一次函数 与 的图象相交于点 ,则函数 的图象可能是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 在 中,与 相邻的外角是130°,要使 为等腰三角形,则 的度数是( )A、50° B、65° C、50°或65° D、50°或65°或80°
10. 在 中,与 相邻的外角是130°,要使 为等腰三角形,则 的度数是( )A、50° B、65° C、50°或65° D、50°或65°或80°二、填空题
-
11. 一次函数 的图象与x轴的交点坐标是 .12. 写出命题“如果 ,那么 互为倒数”的逆命题:.13. 如图, 中, , 是 的角平分线,且 ,则 .
 14. 一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b<0的解集是.
14. 一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b<0的解集是. 15. 如图,一个直角三角形纸片 , , 是边 上一点,沿线段 折叠,使点 落在点 处( 在直线 的两侧),当 时,则 °.
15. 如图,一个直角三角形纸片 , , 是边 上一点,沿线段 折叠,使点 落在点 处( 在直线 的两侧),当 时,则 °. 16. 在 中, 是边 上的两点, , ,则 的度数是 .
16. 在 中, 是边 上的两点, , ,则 的度数是 .三、解答题
-
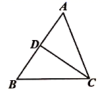
17. 如图, 中, , 是 的中点, ,求 的度数.
 18. 如图(1),在边长为1个单位长度的小正方形组成的4×3的网格中,给出了以格点(网格线的交点)为顶点的格点 ,请在图(2)—(4)中各画出一个与图(1)中 全等但在网格中位置不同的格点三角形.
18. 如图(1),在边长为1个单位长度的小正方形组成的4×3的网格中,给出了以格点(网格线的交点)为顶点的格点 ,请在图(2)—(4)中各画出一个与图(1)中 全等但在网格中位置不同的格点三角形. 19. 已知,如图, 相交于点 , , .
19. 已知,如图, 相交于点 , , .
求证: .
20. 已知,如图,平面直角坐标系中, 是坐标原点,点 ,点 在第四象限, 中 , ,求点 的坐标. 21. 某公司欲将 件产品全部运往甲,乙,丙三地销售(每地均有产品销售),运费分别为40元/件,24元/件,7元/件,且要求运往乙地的件数是运往甲地件数的3倍,设安排 ( 为正整数)件产品运往甲地.(1)、根据信息填表:
21. 某公司欲将 件产品全部运往甲,乙,丙三地销售(每地均有产品销售),运费分别为40元/件,24元/件,7元/件,且要求运往乙地的件数是运往甲地件数的3倍,设安排 ( 为正整数)件产品运往甲地.(1)、根据信息填表:甲地
乙地
丙地
产品件数(件)
运费(元)
(2)、若总运费为6300元,求 与 的函数关系式并求出 的最小值.

