安徽省合肥市包河区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-05 类型:期末考试
一、单选题
-
1. 下列卡通动物简笔画图案中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知三角形的两边长分别为4cm和10cm,则第三边长可以是( )A、13cm B、16cm C、6 cm D、5cm3. 若点P(a-3,a-1)是第二象限的整数点(横、纵坐标都是整数),则a的值为( )A、1 B、2 C、3 D、44. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、
2. 已知三角形的两边长分别为4cm和10cm,则第三边长可以是( )A、13cm B、16cm C、6 cm D、5cm3. 若点P(a-3,a-1)是第二象限的整数点(横、纵坐标都是整数),则a的值为( )A、1 B、2 C、3 D、44. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、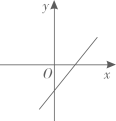 B、
B、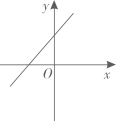 C、
C、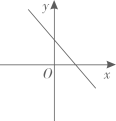 D、
D、 5. 已知方程 解是 ,则直线 与 的交点是( )A、(1,0) B、(1,3) C、(-1,-1) D、(-1,5)6. 在ΔABC和ΔDEF中,AB=DE,∠A=∠D,若证ΔABC≌ΔDEF还要从下列条件中补选一个,错误的选法是( )A、∠B=∠E B、∠C=∠F C、AC=DF D、BC=EF7. 如果一个三角形的三个外角度数的比为1:4:4,则此三角形为( )A、直角三角形 B、锐角三角形 C、饨角三角形 D、黄金三角形8. 如图,已知在△ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
5. 已知方程 解是 ,则直线 与 的交点是( )A、(1,0) B、(1,3) C、(-1,-1) D、(-1,5)6. 在ΔABC和ΔDEF中,AB=DE,∠A=∠D,若证ΔABC≌ΔDEF还要从下列条件中补选一个,错误的选法是( )A、∠B=∠E B、∠C=∠F C、AC=DF D、BC=EF7. 如果一个三角形的三个外角度数的比为1:4:4,则此三角形为( )A、直角三角形 B、锐角三角形 C、饨角三角形 D、黄金三角形8. 如图,已知在△ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )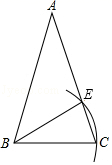 A、AE=EC B、AE=BE C、∠EBC=∠BAC D、∠EBC=∠ABE9. 如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )
A、AE=EC B、AE=BE C、∠EBC=∠BAC D、∠EBC=∠ABE9. 如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( ) A、140° B、100° C、50° D、40°
A、140° B、100° C、50° D、40°二、填空题
-
10. 如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位,元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列正确结论的序号是 .

①第24天的销售量为200件;
②第10天销售一件产品的利润是15元;
③第12天与第30天这两天的日销售利润相等;
④第30天的日销售利润是750元.
11. 命题“两直线平行,内错角相等"的逆命题是一个命题(填“真”或“假”)12. 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x > k1x+b的解集为 13. 如图,在 中,分别以点 和 为圆心,大于 的长为半径画弧,两弧相交于 , ,作直线 ,交 于点 ,连接 。如果 , ,那么 ;
13. 如图,在 中,分别以点 和 为圆心,大于 的长为半径画弧,两弧相交于 , ,作直线 ,交 于点 ,连接 。如果 , ,那么 ; 14. 如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD:DC=3:2,则点D到AB的距离为 .
14. 如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD:DC=3:2,则点D到AB的距离为 . 15. 如图,△ABC≌△ADE,∠EAC=40°,则∠B=°.
15. 如图,△ABC≌△ADE,∠EAC=40°,则∠B=°.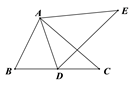 16. 在平面角坐标系中,函数y=2x和y=-x的图像分别为直线l1、l2 , 过点(1,0)作x轴的垂线交l2于点A1 , 过点A1作y轴的垂线交l2于点A2 , 过点A2作x轴的垂线交l1于点A3 , 过点A3作y轴的垂线交l2于点A4 , …,依次进行下去,则点A2020的坐标为
16. 在平面角坐标系中,函数y=2x和y=-x的图像分别为直线l1、l2 , 过点(1,0)作x轴的垂线交l2于点A1 , 过点A1作y轴的垂线交l2于点A2 , 过点A2作x轴的垂线交l1于点A3 , 过点A3作y轴的垂线交l2于点A4 , …,依次进行下去,则点A2020的坐标为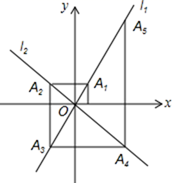
三、解答题
-
17. 如图,已知△ABC .
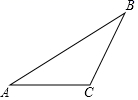 (1)、画出△ABC的高AD;(2)、尺规作出△ABC的角平分线BE(要求保留作图痕迹,不用证明).18. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,4),B(-4,1),C(-1,-1)
(1)、画出△ABC的高AD;(2)、尺规作出△ABC的角平分线BE(要求保留作图痕迹,不用证明).18. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,4),B(-4,1),C(-1,-1) (1)、直接写出△ABC的面积;(2)、在图中作出△ABC关于x轴的对称△A1B1C1;(3)、将△ABC向右平移5个单位,向上平移一个单位,得到△A2B2C2,并写出B2的坐标;19. 为迎接新年,某单位组织员工开展娱乐竞赛活动,工会计划购进A、B两种电器共21件作为奖品.已知A种电器每件90元,B种电器每件70.设购买B种电器x件,购买两种电器所需费用为y元.(1)、y与x的函数关系式为:(2)、若购买B种电器的数量少于A种电器的数量,请给出一种最省费用的方案,并求出该方案所需费用.20. 如图,点C是线段AB上一点,分别以AC和BC为边在线段AB的同侧作等边△ACD和△BCE,连结AE和BD,相交于点F.
(1)、直接写出△ABC的面积;(2)、在图中作出△ABC关于x轴的对称△A1B1C1;(3)、将△ABC向右平移5个单位,向上平移一个单位,得到△A2B2C2,并写出B2的坐标;19. 为迎接新年,某单位组织员工开展娱乐竞赛活动,工会计划购进A、B两种电器共21件作为奖品.已知A种电器每件90元,B种电器每件70.设购买B种电器x件,购买两种电器所需费用为y元.(1)、y与x的函数关系式为:(2)、若购买B种电器的数量少于A种电器的数量,请给出一种最省费用的方案,并求出该方案所需费用.20. 如图,点C是线段AB上一点,分别以AC和BC为边在线段AB的同侧作等边△ACD和△BCE,连结AE和BD,相交于点F.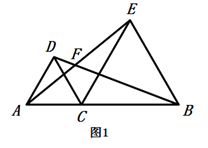
 (1)、求证:AE=BD;(2)、如图2.固定△BCE不动,将等边△ACD绕点C旋转(△ACD和△BCE不重叠),试问∠AFB的大小是否变化?请说明理由;(3)、在△ACD旋转的过程中,以下结论:①CG=CH;② GF=HF; ③FC平分分∠GCH;④FC平分∠GFH;一定正确的有 (填写序号,不要求证明)
(1)、求证:AE=BD;(2)、如图2.固定△BCE不动,将等边△ACD绕点C旋转(△ACD和△BCE不重叠),试问∠AFB的大小是否变化?请说明理由;(3)、在△ACD旋转的过程中,以下结论:①CG=CH;② GF=HF; ③FC平分分∠GCH;④FC平分∠GFH;一定正确的有 (填写序号,不要求证明)