安徽省阜阳市颍州区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-05 类型:期末考试
一、单选题
-
1. 下列图标中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算中正确的是( ).A、 B、 C、 D、3. 下列各式是完全平方式的是( )A、 B、 C、x+xy+1 D、4. 如果分式 中的 x 和y都扩大为原来的 2 倍,那么分式的值( )A、扩大2倍 B、扩大4倍 C、不变 D、缩小2倍5. 如图,点B、F、C、E在一条直线上, , ,要使 ≌ ,需要添加下列选项中的一个条件是( )
2. 下列计算中正确的是( ).A、 B、 C、 D、3. 下列各式是完全平方式的是( )A、 B、 C、x+xy+1 D、4. 如果分式 中的 x 和y都扩大为原来的 2 倍,那么分式的值( )A、扩大2倍 B、扩大4倍 C、不变 D、缩小2倍5. 如图,点B、F、C、E在一条直线上, , ,要使 ≌ ,需要添加下列选项中的一个条件是( )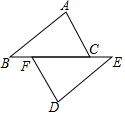 A、 B、 C、 D、6. 如图,在 中, , 于 , ,则 ( )
A、 B、 C、 D、6. 如图,在 中, , 于 , ,则 ( )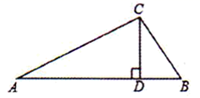 A、 B、 C、 D、7. 若x﹣m与x+3的乘积中不含x的一次项,则m的值为( )A、3 B、1 C、0 D、﹣38. 如果多边形的内角和是外角和的k倍,那么这个多边形的边数是A、k B、 C、 D、9. 如图,在△ABC中,∠ACB=90°, ∠ABC=60°, BD平分∠ABC ,P点是BD的中点,若AD=6, 则CP的长为( )
A、 B、 C、 D、7. 若x﹣m与x+3的乘积中不含x的一次项,则m的值为( )A、3 B、1 C、0 D、﹣38. 如果多边形的内角和是外角和的k倍,那么这个多边形的边数是A、k B、 C、 D、9. 如图,在△ABC中,∠ACB=90°, ∠ABC=60°, BD平分∠ABC ,P点是BD的中点,若AD=6, 则CP的长为( )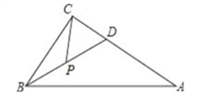 A、3.5 B、3 C、4 D、4.510. 如图,在 中, 面积是16, 的垂直平分线 分别交 边于 点,若点 为 边的中点,点 为线段 上一动点,则 周长的最小值为( )
A、3.5 B、3 C、4 D、4.510. 如图,在 中, 面积是16, 的垂直平分线 分别交 边于 点,若点 为 边的中点,点 为线段 上一动点,则 周长的最小值为( )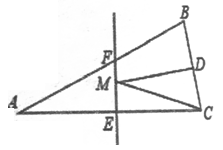 A、6 B、8 C、10 D、12
A、6 B、8 C、10 D、12二、填空题
-
11. 多项式 分解因式的结果是.12. 等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为 .13. 如图,在 中,点 为边 的中点,点 为 上一点,将 沿 翻折,使点 落在 上的点 处,若 ,则 为度.
 14. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O , 过点O作EF∥BC交AB于E , 交AC于F , 过点O作OD⊥AC于D , 下列四个结论:
14. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O , 过点O作EF∥BC交AB于E , 交AC于F , 过点O作OD⊥AC于D , 下列四个结论: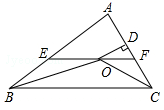
①EF=BE+CF;
②∠BOC=90°+ ∠A;
③点O到△ABC各边的距离相等;
④设OD=m , AE+AF=n , 则 .
其中正确的结论是 . (填序号)
三、解答题
-
15. 计算:(1)、 ;(2)、 .16. 解方程:(1)、(2)、17. 先化简代数式
 ,然后请你自取一组 的值代入求值. 18. 在平面直角坐标系中的位置如图所示.
,然后请你自取一组 的值代入求值. 18. 在平面直角坐标系中的位置如图所示.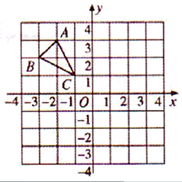 (1)、作出 关于 轴对称的三角形 ,并写出 各顶点的坐标;(2)、将 向下平移3个单位长度,画出平移后的 ,并写出 各顶点的坐标.19. 作图:如图,求作点 ,使点 到 、 两点的距离相等,且 到 两边的距离也相等.(用尺规作图,不写作图步骤,保留作图痕迹)
(1)、作出 关于 轴对称的三角形 ,并写出 各顶点的坐标;(2)、将 向下平移3个单位长度,画出平移后的 ,并写出 各顶点的坐标.19. 作图:如图,求作点 ,使点 到 、 两点的距离相等,且 到 两边的距离也相等.(用尺规作图,不写作图步骤,保留作图痕迹)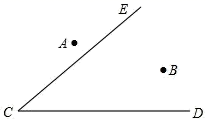 20. 如图,四边形ABCD中,AD∥BC,DE=EC,连结AE并延长交BC的延长线于F,连结BE.
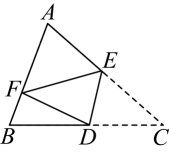
20. 如图,四边形ABCD中,AD∥BC,DE=EC,连结AE并延长交BC的延长线于F,连结BE.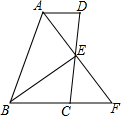 (1)、求证:AD=CF;(2)、若AB=BC+AD,求证:BE⊥AF.21. 如图,点 在 的 边的延长线上, 点在 边上, 交 于点 , , .求证: 是等腰三角形.
(1)、求证:AD=CF;(2)、若AB=BC+AD,求证:BE⊥AF.21. 如图,点 在 的 边的延长线上, 点在 边上, 交 于点 , , .求证: 是等腰三角形.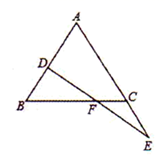 22. 2020年2月22日深圳地铁10号线华南城站试运行,预计今年6月正式开通.在地铁的建设中,某段轨道的铺设若由甲乙两工程队合做,12天可以完成,共需工程费用27720元;已知乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多250元.(1)、求甲、乙两队单独完成这项工程各需多少天?(2)、若工程管理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应选择哪个工程队?请说明理由.23. 如图1,CA=CB,CD=CE,∠ACB=∠DCE=α.
22. 2020年2月22日深圳地铁10号线华南城站试运行,预计今年6月正式开通.在地铁的建设中,某段轨道的铺设若由甲乙两工程队合做,12天可以完成,共需工程费用27720元;已知乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多250元.(1)、求甲、乙两队单独完成这项工程各需多少天?(2)、若工程管理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应选择哪个工程队?请说明理由.23. 如图1,CA=CB,CD=CE,∠ACB=∠DCE=α. (1)、求证:BE=AD;(2)、当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.
(1)、求证:BE=AD;(2)、当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.