安徽省阜阳市临泉县2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-05 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点P(-2,x2+1)所在的象限是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 如图,在平面直角坐标系中,已知点 ,点 ,平移线段AB,使点A落在点 处,则点B的对应点 的坐标为( )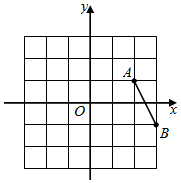 A、 B、 C、 D、3. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
A、 B、 C、 D、3. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. “六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计).下列图象能大致反映战士们离营地的距离S与时间t之间函数关系的是( )A、
4. “六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计).下列图象能大致反映战士们离营地的距离S与时间t之间函数关系的是( )A、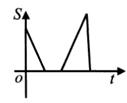 B、
B、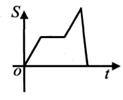 C、
C、 D、
D、 5. 如图,若一次函数y=﹣2x+b的图象与两坐标轴分别交于A,B两点,点A的坐标为(0,3),则不等式﹣2x+b>0的解集为( )
5. 如图,若一次函数y=﹣2x+b的图象与两坐标轴分别交于A,B两点,点A的坐标为(0,3),则不等式﹣2x+b>0的解集为( )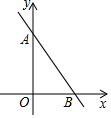 A、x> B、x< C、x>3 D、x<36. 判断命题“如果n<1,那么n2﹣1<0”是假命题,只需举出一个反例.反例中的n可以为( )A、﹣2 B、﹣ C、0 D、7. 若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、3 D、88. 如图,在 中, 平分 交 于点 , , ∠ADC=70° ,则 ∠C 的度数是( )
A、x> B、x< C、x>3 D、x<36. 判断命题“如果n<1,那么n2﹣1<0”是假命题,只需举出一个反例.反例中的n可以为( )A、﹣2 B、﹣ C、0 D、7. 若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、3 D、88. 如图,在 中, 平分 交 于点 , , ∠ADC=70° ,则 ∠C 的度数是( ) A、 B、 C、 D、9. 如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )
A、 B、 C、 D、9. 如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )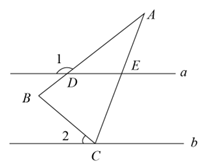 A、30° B、35° C、40° D、45°10.
A、30° B、35° C、40° D、45°10.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( )
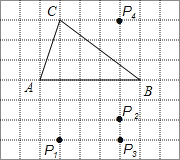 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,已知 ,请你添加一个条件,使得 ,你添加的条件是 . (不添加任何字母和辅助线)
 12. 已知一次函数 的图象经过第一、二、四象限,则 的取值范围是.13. 在△ABC中,∠A=50°,AB=AC,AB的垂直平分线DE交AC于D,则∠DBC的度数是°.14. 在平面直角坐标系中,若点 , ,则 .请在 轴上找一点 ,使 是以 为腰的等腰三角形,点 的坐标为.
12. 已知一次函数 的图象经过第一、二、四象限,则 的取值范围是.13. 在△ABC中,∠A=50°,AB=AC,AB的垂直平分线DE交AC于D,则∠DBC的度数是°.14. 在平面直角坐标系中,若点 , ,则 .请在 轴上找一点 ,使 是以 为腰的等腰三角形,点 的坐标为.三、解答题
-
15. 已知一次函数的图象经过点 , 两点.求这个一次函数的解析式.16. 如图, ,点 在边 上, 与 交于点 ,已知 , ,求 的度数.
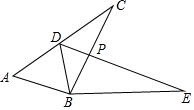 17. 已知:如图,已知点D 是△ABC 的边AB 上一点,点E 为AC 的中点,过点C 作CF∥AB 交DE 延长线于点F.
17. 已知:如图,已知点D 是△ABC 的边AB 上一点,点E 为AC 的中点,过点C 作CF∥AB 交DE 延长线于点F.
求证:DE=EF.
18. 如图, 的三个顶点的坐标分别是 , , .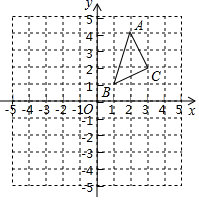 (1)、作出 向左平移 个单位长度,再向下平移 个单位长度后得到的 ,并写出点 的坐标.(2)、作出 关于直线 对称的 ,使点 的对应点为 .(3)、写出直线 的函数解析式为.19. 如图,在 和 中, 、 、 、 在同一直线上,下面有四个条件:
(1)、作出 向左平移 个单位长度,再向下平移 个单位长度后得到的 ,并写出点 的坐标.(2)、作出 关于直线 对称的 ,使点 的对应点为 .(3)、写出直线 的函数解析式为.19. 如图,在 和 中, 、 、 、 在同一直线上,下面有四个条件:
① ;② ;③ ;④ .请你从中选三个作为题设,余下的一个作为结论,写出一个真命题,并加以证明.
解:我写的真命题是:
已知:
求证:(注:不能只填序号)
证明如下:
20. 如图, 中, , ,边 的垂直平分线分别交 、 于 、 两点.试写出线段 和 的数量关系,并给出证明. 21. 已知:如图,一次函数 与 的图象相交于点 .
21. 已知:如图,一次函数 与 的图象相交于点 . (1)、求点 的坐标.(2)、若一次函数 与 的图象与 轴分别相交于点 、 ,求 的面积.(3)、结合图象,直接写出 时 的取值范围.22. 某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
(1)、求点 的坐标.(2)、若一次函数 与 的图象与 轴分别相交于点 、 ,求 的面积.(3)、结合图象,直接写出 时 的取值范围.22. 某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:商品
甲
乙
进价(元/件)
售价(元/件)
200
100
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)、求甲、乙两种商品的进价是多少元?(2)、若超市销售甲、乙两种商品共50件,其中销售甲种商品为 件( ),设销售完50件甲、乙两种商品的总利润为 元,求 与 之间的函数关系式,并求出 的最小值.23. 如图,已知等边三角形 中,点 , , 分别为各边中点, 为直线 上一动点, 为等边三角形(点 的位置改变时, 也随之整体移动). (1)、如图1,当点 在点 左侧时,请判断 与 有怎样的数量关系?请直接写出结论,不必证明或说明理由;(2)、如图2,当点 在 上时,其它条件不变,(1)的结论中 与 的数量关系是否仍然成立?若成立,请利用图2证明;若不成立,请说明理由;(3)、若点 在点 右侧时,请你在图3中画出相应的图形,并判断(1)的结论中 与 的数量关系是否仍然成立?若成立,请直接写出结论,不必证明或说明理由.(提示:连接 、 、 .可证 、 、 、 均为等边三角形).
(1)、如图1,当点 在点 左侧时,请判断 与 有怎样的数量关系?请直接写出结论,不必证明或说明理由;(2)、如图2,当点 在 上时,其它条件不变,(1)的结论中 与 的数量关系是否仍然成立?若成立,请利用图2证明;若不成立,请说明理由;(3)、若点 在点 右侧时,请你在图3中画出相应的图形,并判断(1)的结论中 与 的数量关系是否仍然成立?若成立,请直接写出结论,不必证明或说明理由.(提示:连接 、 、 .可证 、 、 、 均为等边三角形).