广西防城港市上思县2021届九年级上学期数学第一次月考试卷（一）

试卷更新日期：2020-11-05 类型：月考试卷

进入 出卷网 下载

一、选择题（共12道小题，每小题3分，共36分。）

  • 1. 下列方程为一元二次方程的是（ ）
    A、ax2+bx+c=0 B、x2－2x－3 C、2x2＝0 D、xy＋1＝0

    查看试题解析

  • 2. 下列各式中，y是x的二次函数的是(     )

    A、y=1x2 B、y=2x+1 C、y=x2+x-2 D、y2=x2+3x

    查看试题解析

  • 3. 若关于x的一元二次方程(a＋1)x2＋x＋a2－1＝0的一个解是x＝0，则a的值为（   ）
    A、1 B、－1 C、±1 D、0

    查看试题解析

  • 4. 方程(x-2)(x+3)=0的解是（）

    A、x=2 B、x=-3 C、x1=-2,x2=3 D、x1=2,x2=-3

    查看试题解析

  • 5. 把方程x2-6x-5=0左边配成一个完全平方式后,所得的方程是（   ）
    A、(x-6)2=41 B、(x-3)2=4 C、(x-3)2=14 D、(x-3)2=9

    查看试题解析

  • 6. 下列关于x的方程有实数根的是（   ）
    A、x2-x+1=0 B、x2+x+1=0 C、(x-1)(x+2)=0 D、(x-1)2+1=0

    查看试题解析

  • 7. 等腰三角形的底和腰是方程x2-6x+8=0的两个根,则这个三角形的周长是（   ）
    A、8 B、10 C、8或10 D、18

    查看试题解析

  • 8. 将抛物线y=x2向左平移2个单位，再向下平移5个单位，平移后所得新抛物线的表达式为（    ）
    A、y=（x+2）2﹣5 B、y=（x+2）2+5 C、y=（x﹣2）2﹣5 D、y=（x﹣2）2+5

    查看试题解析

  • 9. 目前我国已建立了比较完善的经济困难学生资助体系，某校去年上半年发放给每个经济困难学生389元，今年上半年发放了438元，设每半年发放的资助金额的平均增长率为x，则下面列出的方程中正确的是（   ）

    A、438（1+x）2=389 B、389（1+x）2=438   C、389（1+2x）=438 D、438（1+2x）=389

    查看试题解析

  • 10. 若x2-kx+4是一个完全平方式,则k的值为（   ）
    A、－2 B、2或－2 C、－4 D、4或－4

    查看试题解析

  • 11. 二次函数y＝ax2＋bx＋c的图象如图所示，那么一次函数y＝ax＋b的图象大致是（   ）

    A、 B、 C、 D、

    查看试题解析

  • 12. 如图，二次函数y=ax2+bx+c的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，2）与（0，3）之间（不包括这两点），对称轴为直线x=2．下列结论：abc＜0；②9a+3b+c＞0；③若点M（ 12 ，y1），点N（ 52 ，y2）是函数图象上的两点，则y1＜y2；④﹣ 35 ＜a＜﹣ 25 ．其中正确结论有（   ）

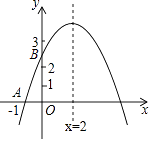    A、1个 B、2个 C、3个 D、4个

    查看试题解析

二、填空题（共6道小题，每小题3分，共18分。）

  • 13. 把方程(x-1)(x-2)=4化成一般形式是.

    查看试题解析

  • 14. 抛物线y=2(x+2)2+4的顶点坐标为

    查看试题解析

  • 15. 抛物线y＝2x2＋8x＋m与x轴只有一个公共点，则m的值为.

    查看试题解析

  • 16. 如图所示，抛物线y=ax2+bx+c（a≠0）与x轴的两个交点分别为A（-1，0）和B（2，0），当y＜0时，x的取值范围是 .

    查看试题解析

  • 17. 国庆节时，某班一个小组有x人，他们每两人之间互送贺卡一张，已知全组 共送贺卡110张，则可列方程为.

    查看试题解析

  • 18. 如图，每个正方形由边长为1的小正方形组成，正方形中黑色、白色小正方形的排列规律如图所示，在边长为n(n≥1)的正方形中，设黑色小正方形的个数为P1 ， 白色小正方形的个数为P2 ， 当偶数n＝时，P2＝5P1.

    查看试题解析

三、解答题：（本大题有8道小题，共66分。）

  • 19. 解下列方程：
    (1)、x2-2x-8=0;
    (2)、x(x－4)＝2－8x.

    查看试题解析

  • 20. 已知二次函数y=- 12 x2+bx+c的图象经过A(2，0)，B(0，-6)两点.

    (1)、求这个二次函数的解析式；
    (2)、设该二次函数图象的对称轴与x轴交于点C，连接BA，BC，求△ABC的面积.

    查看试题解析

  • 21. 已知关于x的一元二次方程(a＋c)x2＋2bx＋(a－c)＝0，其中a、b、c分别为△ABC三边的长．
    (1)、如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
    (2)、如果△ABC是等边三角形，试求这个一元二次方程的根．

    查看试题解析

  • 22. 某西瓜经营户以2元/千克的进价购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售,经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克,另外,每天的房租等固定成本共24元,该经营户要想每天赢利200元,应将每千克小型西瓜的售价降低多少元?

    查看试题解析

  • 23. 已知关于x的方程 x2 －2（k＋2）x＋ k2 －2k－2=0.
    (1)、若这个方程有实数根，求k的取值范围.
    (2)、若这个方程有实数根x=1，求k的值

    查看试题解析

  • 24. 随着人们环保意识的不断增强,我市家庭电动自行车的拥有量逐年增加.据统计,某小区2016年底拥有家庭电动自行车125辆,2018年底家庭电动自行车的拥

    有量达到180辆.

    (1)、若该小区2016年底到2019年底家庭电动自行车拥有量的年平均增长率相同,则该小区到2019年底家庭电动自行车将达到多少辆?
    (2)、为了缓解停车矛盾,该小区决定投资3万元再建若干个停车位,据测算,建造费用分别为室内车位1000元/个,露天车位200元/个.考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,则该小区最多可建两种车位各多少个?试写出所有可能的方案.

    查看试题解析

  • 25. 九(1)班数学兴趣小组经过市场调查，整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表：

    时间x(天)

    1≤x＜50

    50≤x≤90

    售价(元/件)

    x＋40

    90

    每天销量(件)

    200－2x

    已知该商品的进价为每件30元，设销售该商品的每天利润为y元．

    (1)、求出y与x的函数关系式；
    (2)、问销售该商品第几天时，当天销售利润最大，最大利润是多少？
    (3)、该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．

    查看试题解析

  • 26. 已知抛物线经过点A(－1，0)，B( 3，0)，C( 0，3)三点．

    (1)、求抛物线的解析式；
    (2)、点M是线段BC上的点(不与B，C重合)，过M作NM∥y轴交抛物线于N，若点M的横坐标为m，请用含m的代数式表示MN的长；
    (3)、在(2)的条件下，连接NB，NC，是否存在点m，使△BNC的面积最大？若存在，求m的值；若不存在，说明理由．

    查看试题解析