广西防城港市上思县2020-2021学年八年级上学期数学第一次月考试卷（一）
试卷更新日期：2020-11-05 类型：月考试卷
一、选择题（共12道小题，每小题3分，共36分。）
-
1. 以下列各组线段为边，能组成三角形的是（ ）A、2cm，3cm，5cm B、5cm，6cm，10cm C、1cm，1cm，3cm D、3cm，4cm，9cm2. 等腰三角形的一边长等于4，一边长等于9，则它的周长是（ ）A、13 B、17 C、22 D、17或223. 适合条件∠A＝ ∠B＝ ∠C的△ABC是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形4. 已知等腰三角形的一个角为75°，则其顶角为（ ）A、30° B、75° C、105° D、30°或75°5. 一个多边形的内角和比它的外角的和的2倍还大180°，这个多边形的边数是（ ）A、5 B、6 C、7 D、86. 三角形的一个外角是锐角，则此三角形的形状是（ ）A、锐角三角形 B、钝角三角形 C、直角三角形 D、等腰三角形7. 下列说法： ①全等三角形的形状相同、大小相等 ②全等三角形的对应边相等、对应角相等③面积相等的两个三角形全等 ④全等三角形的周长相等，其中正确的说法是（ ）A、①②③④ B、①②③ C、②③④ D、①②④8. 装修工人在搬运中发现有一块三角形的陶瓷片不慎摔成了四块（如图所示），他要拿哪一块回公司才能更换到相匹配的陶瓷片（ ）
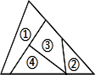A、① B、② C、③ D、④9. 工人师傅常用角尺平分一个任意角．做法如下：如图所示，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合．过角尺顶点C的射线OC即是∠AOB的平分线．这种做法的道理是（ ）
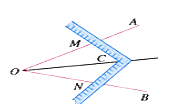A、HL B、SSS C、SAS D、ASA10. 如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，DE=2，AC=3，则△ADC的面积是（ ）
A、3 B、4 C、5 D、611. 如图，如果AD∥BC，AD=BC，AC与BD相交于O点，则图中的全等三角形一共有（ ）
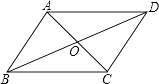A、3对 B、4对 C、5对 D、6对12. 已知：如图在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点同一条直线上，连接BD，BE.以下四个结论：①BD=CE； ②BD⊥CE； ③∠ACE+∠DBC=45°；④∠BAE＋∠DAC＝180°.
其中结论正确的个数是（ ）
A、1 B、2 C、3 D、4二、填空题（共6道小题，每小题3分，共18分。）
-
13. 多边形的外角和等于度.14. 如果两个图形全等，那么它们的面积.15. 如图，已知△AOC≌△BOC，∠AOB=70°，则∠1=.
16. 如图，AD⊥BC，∠1=∠2，∠C=65°，则∠BAC =°
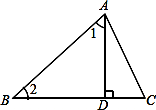17. 如图，BE⊥AC，垂足为D，且AD＝CD，BD＝ED.若∠ABC＝54°， 则∠BEC＝°.
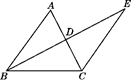18. 如图所示，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm.沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为cm.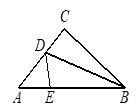
三、解答题：（本大题有8道小题，共66分。）
-
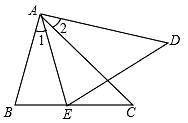
19. 如图，AB=AE，∠B=∠AED，∠1=∠2．求证：△ABC≌△AED.
20. 阅读并理解下面的证明过程，并在每步后的括号内填写该步推理的依据.已知：如图，AM，BN，CP是△ABC的三条角平分线.
求证：AM、BN、CP交于一点.
证明：如图，设AM，BN交于点O，过点O分别作OD⊥BC，OF⊥AB，垂足分别为点D，E，F.
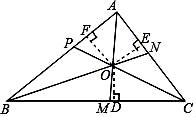
∵O是∠BAC角平分线AM上的一点（ ），
∴OE=OF（ ）.
同理，OD=OF.
∴OD=OE（ ）.
∵CP是∠ACB的平分线（ ），
∴O在CP上（ ）.
因此，AM，BN，CP交于一点.
21. 如图所示，若BE＝CD，∠1＝∠2，则BD与CE相等吗?为什么?
22. 已知：如图所示，点B，E，C，F在同一直线上，AB=DE，AC=DF，BE=CF.求证：∠A=∠D
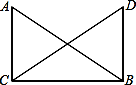
23. 如图，已知AC⊥CB于C，DB⊥CB于B，AB=DC.求证：∠ABD=∠ACD.
24. 如图所示，在△ABC中，∠C＝90°，AD是∠BAC的平分线，DE⊥AB交AB于点E，点F在AC上，BD＝DF.
求证：
(1)、CF＝EB；(2)、AB＝AF＋2EB.
