江苏省苏州市园区一中2020-2021学年七年级上学期数学10月月考试卷

试卷更新日期：2020-11-05 类型：月考试卷

进入出卷网下载

一、单选题

1. $- \frac{4}{5}$ 的相反数是（）

A、 $\frac{5}{4}$ B、 $\frac{4}{5}$ C、 $- \frac{4}{5}$ D、 $- \frac{5}{4}$

查看试题解析
2. 国家提倡“低碳减排”，某公司计划在海边建风能发电站，发电站年均发电量为213000000度，将数据213000000用科学记数法表示为（）

A、213×10⁶ B、21.3×10⁷ C、2.13×10⁸ D、2.13×10⁹

查看试题解析
3. 下列各数： $- \frac{7}{4}, 1.010010001, \frac{8}{33}, 0, - π, - 2.626626662 \dots, 0.1 \dot{2},$ 其中有理数的个数是（）

A、3 B、4 C、5 D、6

查看试题解析
4. 若（x-1）² + |y + 2| = 0，则x + y的值等于（）

A、- 3 B、3 C、- 1 D、1

查看试题解析
5. 已知有理数a，b满足|a| =- a，|b| = b，|a| > |b|，则a，b在数轴上的位置表示正确的是（）

A、 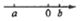B、 C、 D、

查看试题解析
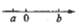6. 如图是一个简单的数值计算程序，当输入的x的值为5时，输出的结果为（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、2 D、 $\frac{1}{2}$

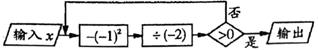查看试题解析
7. 计算1+（-2）+3+（-4）+...+97+(-98)+ 99+（-100）的值为（）

A、50 B、- 50 C、101 D、- 101

查看试题解析
8. 下列说法错误的是（）

A、任何有理数都有倒数 B、互为倒数的两个数积为1 C、互为倒数的两个数同号 D、-3和 $- \frac{1}{3}$ 互为倒数

查看试题解析
9. 如果a，b，c为非零有理数且a + b + c = 0，那么 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |} + \frac{a b c}{| a b c |}$ 的所有可能的值为（）

A、0 B、1或- 1 C、2或- 2 D、0或- 2

查看试题解析
10. 计算：3¹+1 = 4，3² + 1 = 10，3³ + 1 = 28，3⁴ + 1 = 82，3⁵+1 = 244，…，归纳计算结果中的个位数字的规律，猜测3²⁰²⁰ + 1的个位数字是（）

A、0 B、2 C、4 D、8

查看试题解析

二、填空题

11. 计算： $- {(- 3)}^{2}$ ＝.

查看试题解析
12. 比较大小： $- \frac{2}{3}$ $- \frac{3}{4}$ （填“ > ”“ < ” = “）

查看试题解析
13. 绝对值不大于 $3 \frac{1}{2}$ 的所有整数的和为.

查看试题解析
14. 已知|a|=5，b²=16，且ab＜0，那么a﹣b的值为．

查看试题解析
15. 有一列数 $- \frac{1}{2} ， \frac{2}{5} ， - \frac{3}{10} ， \frac{4}{17} ，$ …，那么第7个数是．

查看试题解析
16. 若a、b互为相反数，c、d互为倒数，m的绝对值为2，则 $\frac{a + b}{3} + c d + m^{2} =$

查看试题解析
17. 某班5名学生在一次数学测试中的成绩以90为标准，超过的分数记为正数，不足的分数记为负数，记录如下：-4，+9，-1， 0，+6，则他们的平均成绩是分

查看试题解析
18. 在数轴上点A表示的数是a，点B表示的数是b，且a，b满足 $| a + 2 | + {(b + 1)}^{2} = 0$ 点C表示的数是7.若将数轴折叠，使得点A与点C重合，则与点B重合的点表示的数是 .

查看试题解析

三、解答题

19. 在数轴上表示下列各数，并用“＜”号把它们按照从小到大的顺序排列.3，﹣（﹣1），﹣1.5，0， $- | - 2 |$ ， $- 3 \frac{1}{2}$

查看试题解析
20. 计算

(1)、 $7 + (- 4) - 3$

(2)、 $- 3 \div (- 5) \times \frac{1}{5}$

(3)、 $9 + 5 \times (- 3) - {(- 2)}^{2} \div 4$

(4)、 ${(- 1)}^{4} - [2 - {(- 3)}^{2}]$

(5)、 $(\frac{1}{3} + \frac{1}{2} - \frac{5}{6} - \frac{3}{4}) \div {(- \frac{1}{3})}^{2}$

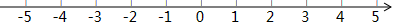(6)、 $19 \frac{13}{14} \times (- 14)$

查看试题解析
21. 把下列各数填入相应集合的括号内： $2013, \frac{22}{7}, 3.1415926, 0, - 2 \frac{1}{3}, \frac{π}{4}, - | - 12 |, - 0.101001000...$

(1)、正数集合：{                                                 …}

(2)、负数集合：{                                                 …}

(3)、有理数集合：{                                               …}

(4)、无理数集合：{                                               …}

查看试题解析
22. 已知，|a| = 3，|b| = 2，且ab < 0，求：a + b的值.

查看试题解析
23. 我们定义一种新运算：a*b=a²-b+ab.

(1)、求2*(-3)的值.

(2)、求(-2)*[2*(-3)]的值.

查看试题解析
24. a、b互为相反数，c、d互为倒数，数轴上表示m的点到原点距离为4，求 $\frac{a + b}{m}$ +cd-m的值．

查看试题解析
25. 同学们都知道， $| 5 - (- 2) |$ 表示5与－2之差的绝对值，实际上也可理解为5与－2两数在数轴上所对应的两点之间的距离，试探索：

(1)、求 $| 5 - (- 2) |$ ＝．

(2)、若 $| x - 2 | = 5$ ，则 $x$ =

(3)、同理 $| x + 1 | + | x - 2 |$ 表示数轴上有理数x所对应的点到－1和2所对应的两点距离之和，请你找出所有符合条件的整数x，使得 $| x + 1 | + | x - 2 | = 3$ ，这样的整数是(直接写答案)

查看试题解析
26. 有30箱苹果，以每箱20千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：

(1)、这30箱苹果中，最重的一箱比最轻的一箱重多少千克?

(2)、与标准质量比较，这30箱苹果总计超过或不足多少千克?

(3)、若苹果每千克售价6元，则出售这30箱苹果可卖多少元?

查看试题解析
27. 观察下列等式的规律，解答下列问题：
$① 3^{2} - 3^{1} = 2 \times 3^{1} ；$ $② 3^{3} - 3^{2} = 2 \times 3^{2}$ $③ 3^{4} - 3^{3} = 2 \times 3^{3}$ $\dots$

(1)、按此规律，第④个等式为；第 $n$ 个等式为；（用含 $n$ 的代数式表示， $n$ 为正整数）

(2)、按此规律，计算：
$① ： 2 \times 3^{1} + 2 \times 3^{2} + 2 \times 3^{3} + 2 \times 3^{4} + 2 \times 3^{5} ；$

$② ： 3^{1} + 3^{2} + 3^{3} + \dots + 3^{n} .$

查看试题解析
28. 如图，在数轴上点 $A$ 表示的数是 $- 3 ；$ 点 $B$ 在点 $A$ 的右侧，且到点 $A$ 的距离是18；点 $C$ 在点 $A$ 与点 $B$ 之间，且到点 $B$ 的距离是到点 $A$ 距离的2倍.

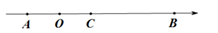
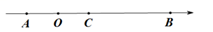(1)、点 $B$ 表示的数是；点 $C$ 表示的数是；

(2)、若点P从点 $A$ 出发，沿数轴以每秒4个单位长度的速度向右匀速运动；同时，点Q从点B出发，沿数轴以每秒2个单位长度的速度向左匀速运动。设运动时间为 $t$ 秒，在运动过程中，当 $t$ 为何值时，点P与点Q之间的距离为6？

(3)、在（2）的条件下，若点P与点C之间的距离表示为PC，点Q与点B之间的距离表示为 $Q B ，$ 在运动过程中，是否存在某一时刻使得 $P C + Q B = 4$ ？若存在，请求出此时点 $P$ 表示的数；若不存在，请说明理由.

查看试题解析