初中数学苏科版九年级上册第四章 等可能条件下的概率 单元测试
试卷更新日期：2020-11-04 类型：单元试卷
一、单选题
-
1. 投掷一枚普通的正方体骰子，有下列事件：①掷得的点数是6；②掷得的点数是奇数；③掷得的点数不大于4；④掷得的点数不小于2，这些事件发生的可能性由大到小排列正确的是（ ）.A、①②③④ B、④③②① C、③④②① D、②③①④2. 一个质地均匀的小正方体的六个面上分别标有数字1，2，3，4，5，6.如果任意抛掷小正方体两次，那么下列说法正确的是（ ）.A、得到的数字和必然是4 B、得到的数字和可能是3 C、得到的数字和不可能是2 D、得到的数字和有可能是13. 已知电流在一定时间段内正常通过电子元件“
”的概率是0.5；则在一定时间段内，由该元件组成的图示电路A、B之间，电流能够正常通过的概率是（ ） 
A、0.75 B、0.625 C、0.5 D、0.254. 已知一个质地均匀的正四面体的每个面上分别标有1，2，3，4四个数字，抛掷这个正四面体，则接地的那一面为偶数的概率为（ ）A、 B、 C、 D、5. 如图，飞镖游戏板中每一块小正方形除颜色外都相同。若一个人向游戏板投掷飞镖一次(假设飞镖落在游戏板上)，则飞镖落在阴影部分的概率是（ ）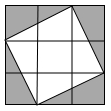
A、 B、 C、 D、6. 一个不透明的袋子中有3个白球、2个黄球和1个红球，这些球除颜色外其他完全相同，那么从袋子中随机摸出一个球是黄球的概率为（ ）A、 B、 C、 D、7. 一个密码箱的密码，每个位数上的数都是从0到9的自然数，若要使不知道密码的一次就拨对密码的概率小于 ，则密码的位数至少需要（ ）位．A、3位 B、2位 C、9位 D、10位8. 从九（1）班2名优秀班干部和九（2）班2名优秀班干部中，随机选取两名学生担任升旗手，则选取的两名升旗手不是同一个班的概率为（ ）A、 B、 C、 D、9. 一只昆虫在如图所示的树枝上寻觅食物，假定昆虫在每个岔路口都会随机选择一条路径，则它获取食物的概率是（ ）
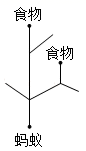A、 B、 C、 D、10. 如图所示，小明、小刚利用两个转盘进行游戏，规则为小明将两个转盘各转一次，如配成紫色（红与蓝），小明胜，否则小刚胜，此规则（ ）
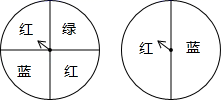A、公平 B、对小明有利 C、对小刚有利 D、公平性不可预测二、填空题
-
11. 一个不透明的盒子里放置三张完全相同的卡片，分别标有数字1，2，3．随机抽取1张，放回后再随机抽取1张，则抽得的第二张卡片上的数字大于第一张卡片上的数字的概率为 ．12. 口袋内装有大小、质量和材料都相同的两种颜色的球，其中红色球3个，白色球2个，从中任意摸出一球，摸出白色球的概率是 ．13. 在一个不透明的袋子中有 个红球、 个绿球和 个白球，这些球除颜色外都相同，摇匀后从袋子中任意摸出一个球，摸出颜色的球的可能性最大.14. 桌子上有6杯同样型号的杯子，其中1杯白糖水，2杯矿泉水，3杯凉白开，从6个杯子中随机取出1杯，请你将下列事件发生的可能性从大到小排列： ．（填序号即可）①取到凉白开 ②取到白糖水 ③取到矿泉水 ④没有取到矿泉水15. 向如图所示的正三角形区域扔沙包(区域中每一个小正三角形除颜色外完全相同)，假设沙包击中每一个小三角形是等可能的，扔沙包1次击中阴影区域的概率等于.
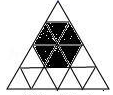16. 如图，一块飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖，击中黑色区域的概率是 ．
17. 如图，电路图上有四个开关A、B、C、D和一个小灯泡，在开关全部断开的情况下，闭合其中任意一个开关，灯泡发亮的概率是；若闭合其中任意两个开关，灯泡发亮的概率是.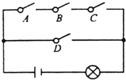
18. 从1，2，3，4四个数中任意取出2个数做加法，其和为偶数的概率是 ．三、解答题
-
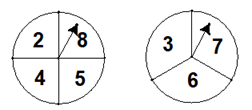
19. 一个不透明的口袋中装有 个红球和 个白球，小球除颜色外其余均相同．从口袋中随机摸出一个小球，记下颜色后放回，再随机摸出一个小球．请用画树状图(或列表) 的方法，求两次摸出的小球颜色不同的概率．20. 如图，两个转盘分别被分成四等分和三等分，并标有数字。旋转停止时，每个转盘上的箭头各指向一个数字，通过树状图或列表法求这两个数字之和为偶数的概率．
21. 甲口袋中装有红色、绿色两把扇子，这两把扇子除颜色外无其他差别；乙口袋中装有红色、绿色两条手绢，这两条手绢除颜色外无其他差别．从甲口袋中随机取出一把扇子，从乙口袋中随机取出一条手绢，用画树状图或列表的方法，求取出的扇子和手绢都是红色的概率．
22. 一个不透明的口袋中装有三个完全相同的小球，上面分别标有数字 ，5．(1)、从口袋中随机摸出一个小球，求摸出小球上的数字是无理数的概率（直接写出结果）；(2)、先从口袋中随机摸出一个小球，将小球上的数字记为x，把小球放回口袋中并搅匀，再从口袋中随机摸出一个小球，将小球上的数字记为y．请用列表法或画树状图法求出x与y的乘积是有理数的概率．23. 从2021年起，江苏省高考采用“ ”模式：“3”是指语文、数学、外语3科为必选科目，“1”是指在物理、历史2科中任选科，“2”是指在化学、生物、思想政治、地理4科中任选2科.(1)、若小丽在“1”中选择了历史，在“2”中已选择了地理，则她选择生物的概率是；(2)、若小明在“1”中选择了物理，用画树状图的方法求他在“2中选化学、生物的概率.24. “2020第二届贵阳市应急科普知识大赛”的比赛中有一个抽奖活动.规则是：准备3张大小一样，背面完全相同的卡片，3张卡片的正面所写内容分别是《消防知识手册》《辞海》《辞海》，将它们背面朝上洗匀后任意抽出一张，抽到卡片后可以免费领取卡片上相应的书籍.(1)、在上面的活动中，如果从中随机抽出一张卡片，记下内容后不放回，再随机抽出一张卡片，请用列表或画树状图的方法，求恰好抽到2张卡片都是《辞海》的概率；(2)、再添加几张和原来一样的《消防知识手册》卡片，将所有卡片背面朝上洗匀后，任意抽出一张，使得抽到《消防知识手册》卡片的概率为 ，那么应添加多少张《消防知识手册》卡片？请说明理由.25. 某汽车公司为了解某型号汽车在同一条件下的耗油情况，随机抽取了n辆该型号汽车耗油 所行使的路程作为样本，并绘制了以下不完整的频数分布直方图和扇形统计图．根据题中已有信息，解答下列问题：
(1)、求n的值，并补全频数分布直方图；(2)、若该汽车公司有600辆该型号汽车，试估计耗油 所行使的路程低于 的该型号汽车的辆数；(3)、从被抽取的耗油 所行使路程在 ， 这两个范围内的4辆汽车中，任意抽取2辆，求抽取的2辆汽车来自同一范围的概率．26. 如图，现有一个均匀的转盘被平均分成6等份，分别标有数字2、3、4、5、6、7这六个数字，转动转盘，当转盘停止时，指针指向的数字即为转出的数字.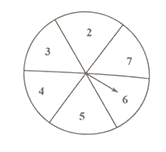
求：
(1)、转动转盘，转出的数字大于3的概率是多少？(2)、现有两张分别写有3和4的卡片，随机转动转盘，转盘停止后记下转出的数字，与两张卡片上的数字分别作为三条线段的长度.①这三条线段能构成三角形的概率是.
②这三条线段能构成等腰三角形的概率是.