初中数学苏科版九年级上册第三章数据的集中趋势和离散程度单元测试

试卷更新日期：2020-11-04 类型：单元试卷

进入出卷网下载

一、单选题

1. 在课外活动中，有10名同学进行了投篮比赛，限每人投10次，投中次数与人数如下表：

投中次数

5

7

8

9

10

人数

2

3

3

1

1

则这10人投中次数的平均数和中位数分别是（）

A、 $3.9 ， 7$ B、 $6.4 ， 7.5$ C、 $7.4 ， 8$ D、 $7.4 ， 7.5$

查看试题解析
2. 某校评选先进班集体，从“学习”、“卫生”、“纪律”、“活动参与”四个方面考核打分，各项满分均为 $100$ ，所占比例如下表：

项目

学习

卫生

纪律

活动参与

所占比例

$40 %$

$25 %$

$25 %$

$10 %$

八年级2班这四项得分依次为80，90，84，71，则该班四项综合得分（满分100）为（）

A、81.5 B、82.5 C、84 D、86

查看试题解析
3. 两组数据：3，a ， b ， 5与a ， 4， $2 b$ 的平均数都是3．若将这两组数据合并为一组新数据，则这组新数据的众数为（）

A、2 B、3 C、4 D、5

查看试题解析
4. 方差是刻画数据波动程度的量，对于一组数据x1，x2，x3，xn，可用如下算式计算方差： $s^{2} = \frac{1}{n} [{(x_{1} - 5)}^{2} + {(x_{2} - 5)}^{2} + {(x_{3} - 5)}^{2} + ...... + {(x_{n} - 5)}^{2}]$ ，其中“5”是这组数据的（）

A、最小值 B、平均数 C、中位数 D、众数

查看试题解析
5. 为调动学生参与体育锻炼的积极性，某校组织了一分钟跳绳比赛活动，体育组随机抽取了10名参赛学生的成绩，将这组数据整理后制成统计表：

一分钟跳绳个数（个）

141

144

145

146

学生人数（名）

5

2

1

2

则关于这组数据的结论正确的是（）

A、平均数是144 B、众数是141 C、中位数是144.5 D、方差是5.4

查看试题解析
6. 已知一组数据5，4，3，4，9，关于这组数据的下列描述：
①平均数是5，②中位数是4，③众数是4，④方差是4.4，其中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

7. 某鞋店试销一种新款男鞋，试销期间销售情况如下表：

鞋的尺码（ $c m$ ）	$24$	$24.5$	$25$	$25.5$	$26$	$26.5$
销售数量（双）	$2$	$7$	$18$	$10$	$8$	$3$

则该组数据的下列统计量中，对鞋店下次进货最具有参考意义的是（）

A、中位数 B、平均数 C、众数 D、方差

查看试题解析

8. 下图描述了某车间工人日加工零件数的情况，这些工人日加工零件数的中位数为（）.

A、4 B、5 C、6 D、7

查看试题解析

9. 格桑同学一周的体温监测结果如下表：

星期	一	二	三	四	五	六	日
体温（单位：℃）	36.6	35.9	36.5	36.2	36.1	36.5	36.3

分析上表中的数据，众数、中位数、平均数分别是（）

A、35.9，36.2，36.3 B、35.9，36.3，36.6 C、36.5，36.3，36.3 D、36.5，36.2，36.6

查看试题解析

10. 某一公司共有51名员工（包括经理），经理的工资高于其他员工的工资，今年经理的工资从去年的200000元增加到225000元，而其他员工的工资同去年一样，这样，这家公司所有员工今年工资的平均数和中位数与去年相比将会（）

A、平均数和中位数不变 B、平均数增加，中位数不变 C、平均数不变，中位数增加 D、平均数和中位数都增大

查看试题解析

二、填空题

11. 临近中考，报考体育专项的同学利用课余时间紧张地训练，甲、乙两名同学最近20次立定跳远成绩的平均值都是 $2.58 m$ ，方差分别是： $s_{甲}^{2} = 0.075, s_{乙}^{2} = 0.04$ ，这两名同学成绩比较稳定的是（填“甲”或“乙”）.

查看试题解析

12. 某公司有10名员工，他们所在部门及相应每人所创年利润如下表所示。

部门	人数	每人所创年利润/万元
A	1	10
B	2	8
C	7	5

这个公司平均每人所创年利润是万元。

查看试题解析

13. 某校招聘教师，其中一名教师的笔试成绩是80分，面试成绩是60分，综合成绩笔试占60%，面试占40%，则该教师的综合成绩为分．

查看试题解析
14. 已知一组数据－3，x，－2，3，2，6的中位数为2，则其众数是.

查看试题解析
15. 一组数据2，3，x，y，12中，唯一的众数是12，平均数是6，则这组数据的中位数是．

查看试题解析

16. 八年级一、二班的同学在一次数学测验中的成绩统计情况如下表：

班级	参加人数	中位数	平均数	方差
一	50	84	80	186
二	50	85	80	161

某同学分析后得到如下结论：①一，二班学生成绩平均水平相同；②二班优生人数不少于一班（优生线85分）；③一班学生的成绩相对稳定，其中正确的是．（填序号）

查看试题解析

17. 2020年春季复学各校采取年级错时用餐，某校为了了解学生在校午餐所需的时间，抽查了20名同学在校午餐所花的时间，绘制频数直方图如图所示，则可预估该校学生平均用餐时间为分钟.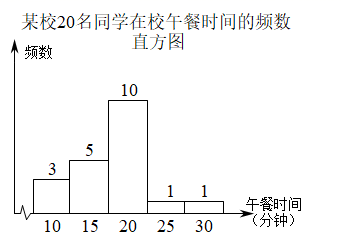

查看试题解析
18. 已知一组数据 $x_{1}, x_{2}, x_{3}, x_{4}, x_{5}$ 的平均数是2，方差是 $\frac{1}{3}$ ，那么另一组数据 $3 x_{1} - 2$ ， $3 x_{2} - 2$ ， $3 x_{3} - 2$ ， $3 x_{4} - 2$ ， $3 x_{5} - 2$ 的平均数是，方差是.

查看试题解析

三、解答题

19. 某公司对应聘者A ， B进行面试，并按三个方面给应聘者打分，每方面满分20分，打分结果如下表：

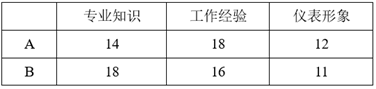
根据实际需要，公司将专业知识、工作经验和仪表形象三项成绩得分按6：1：3的比例确定两人的成绩，通过计算说明谁将被录用．

查看试题解析
20. 某单位若干名职工参加“预防新冠肺炎”卫生知识竞赛，将成绩制成如图所示的扇形统计图和条形统计图，根据图中提供的信息，求这些职工成绩的中位数和平均数.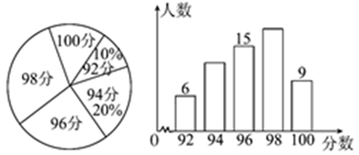

查看试题解析

四、综合题

21. 在学校组织的知识竞赛中，每班参加比赛的人数相同，成绩分为A、B、C、D四个等级，其中相应等级的得分依次记为100分、90分、80分、70分，学校将八年级一班和二班的成绩整理并绘制成如下的统计图：

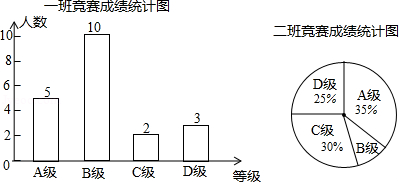
请你根据以上提供的信息解答下列问题：

(1)、求一班参赛选手的平均成绩；

(2)、此次竞赛中，二班成绩在C级以上（包括C级）的人数有几人？

(3)、求二班参赛选手成绩的中位数.

查看试题解析
22. 3月14日是国际数学日，“数学是打开科学大门的钥匙.”为进一步提高学生学习数学的兴趣，某校开展了一次数学趣味知识竞赛（竞赛成绩为百分制），并随机抽取了50名学生的竞赛成绩（本次竞赛没有满分），经过整理数据得到以下信息：
信息一：50名学生竞赛成绩频数分布直方图如图所示，从左到右依次为第一组到第五组（每组数据含前端点值，不含后端点值）.

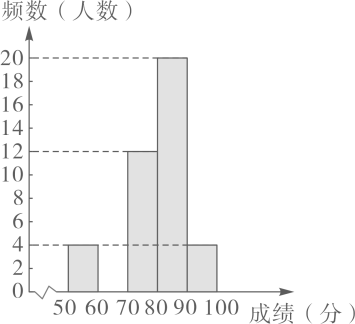
信息二：第三组的成绩（单位：分）为74 71 73 74 79 76 77 76 76 73 72 75

根据信息解答下列问题：

(1)、补全第二组频数分布直方图（直接在图中补全）；

(2)、第三组竞赛成绩的众数是分，抽取的50名学生竞赛成绩的中位数是分；

(3)、若该校共有1500名学生参赛，请估计该校参赛学生成绩不低于80分的约为人.

查看试题解析
23. 2020年2月，贵州省积极响应国家“停课不停学”的号召，推出了“空中黔课”.为了解某中学初三学生每天听空中黔课的时间，随机调查了该校部分初三学生.根据调查结果，绘制出了如下统计图表（不完整），请根据相关信息，解答下列问题：
部分初三学生每天听空中黔课时间的人数统计表

时间/ $h$

1.5

2

2.5

3

3.5

4

人数/人

2

6

6

10

$m$

4

部分初三学生每天听空中黔课时间的人数统计图

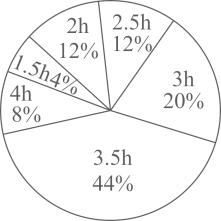(1)、本次共调查的学生人数为，在表格中， $m =$ ；

(2)、统计的这组数据中，每天听空中黔课时间的中位数是，众数是；

(3)、请就疫情期间如何学习的问题写出一条你的看法.

查看试题解析
24. 某校举行了“防溺水”知识竞赛，八年级两个班选派10名同学参加预赛，依据各参赛选手的成绩(均为整数)绘制了统计表和折线统计图(如图所示)．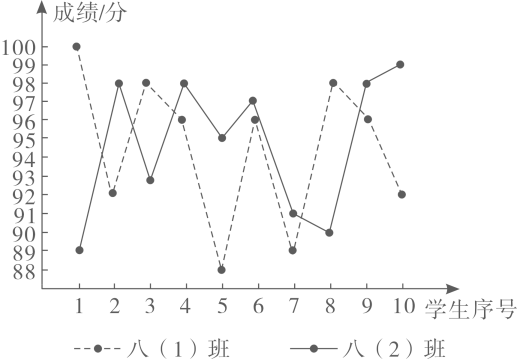

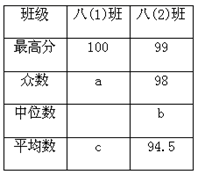(1)、统计表中，a= ， b =；

(2)、若从两个班的预赛选手中选四名学生参加决赛，其中两个班的第一名直接进入决赛，另外两个名额在成绩为98分的学生中任选两个，求另外两个决赛名额落在不同班级的概率．

查看试题解析