初中数学苏科版九年级上册4.3 等可能条件下的概率（二）同步练习
试卷更新日期：2020-11-04 类型：同步测试
一、单选题
-
1. 小华把如图所示的4×4的正方形网格纸板挂在墙上玩飞镖游戏（每次飞镖均落在纸板上，且落在纸板的任何一个点的机会都相等） ，则飞镖落在阴影区域的概率是（ ）
A、 B、 C、 D、2. 四张背面完全相同的卡片，正面分别印有等腰三角形、圆、平行四边形、正六边形，现在把它们的正面向下，随机的摆放在桌面上，从中任意抽出一张，则抽到的卡片正面是中心对称图形的概率是（ ）A、 B、 C、 D、13. 如图①所示，平整的地面上有一个不规则图案（图中阴影部分），小明想了解该图案的面积是多少，他采取了以下办法：用一个长为 ，宽为 的长方形，将不规则图案围起来，然后在适当位置随机地朝长方形区域扔小球，并记录小球落在不规则图案上的次数（球扔在界线上或长方形区域外不计实验结果），他将若干次有效实验的结果绘制成了②所示的折线统计图，由此他估计不规则图案的面积大约为（ ）
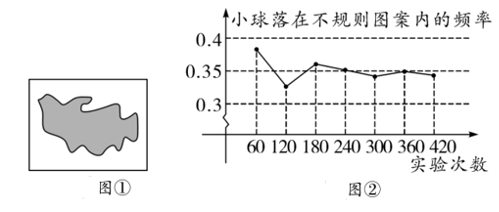A、 B、 C、 D、4. 如果小球在如图所示的地面上自由滚动，并随机停留在某块方砖上，那么它最终停留在黑色区域的概率是（ ）
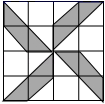A、 B、 C、 D、5. 如图是一个可以自由转动的转盘，转盘分成黑、白两种颜色指针的位置固定，转动的转盘停止后，指针恰好指向白色扇形的穊率为 （指针指向OA时，当作指向黑色扇形；指针指OB时，当作指向白色扇形），则黑色扇形的圆心角∠AOB＝（ ）
A、40° B、45° C、50° D、60°6. 如图把一个圆形转盘按 的比例分成A，B，C，D四个扇形区域，自由转动转盘，停止后指针落在B区域的概率为（ ）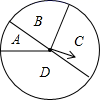
A、 B、 C、 D、7. 如图，“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形，随机在大正方形及其内部区域投针．若针扎到小正方形（阴影部分）的概率是 ，则大、小两个正方形的边长之比是（ ）
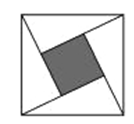A、4：1 B、2：1 C、 ：1 D、1：28. 在边长为1的小正方形组成的4×3网格中，有如图所示的A、B两个格点在格点上任意放置点C，恰好能使△ABC的面积为1的概率是（ ）
A、 B、 C、 D、9. 闵行体育公园内有一个形状是平行四边形的花坛（如图），并且AB∥EF∥DC，BC∥GH∥AD，花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花．如果小杰不小心把球掉入花坛，那么下列说法中错误的是（ ）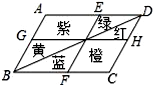
A、球落在红花丛中和绿花丛中的概率相等 B、球落在紫花丛中和橙花丛中的概率相等 C、球落在红花丛中和蓝花丛中的概率相等 D、球落在蓝花丛中和黄花丛中的概率相等10. 如图是两个可以自由转动的转盘，每个转盘被分成两个扇形，同时转动两个转盘，转盘停止后，指针所指区域内的数字之和为4的概率是（ ）
A、 B、 C、 D、二、填空题
-
11. 下图是由全等的小正方形组成的图案，假设可以随意在图中取点，那么这个点取在阴影部分的概率是.
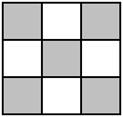12. 一个小球在如图所示的方格地砖上任意滚动，并随机停留在某块地砖上.每块地砖的大小、质地完全相同，那么该小球停留在黑色区域的概率是.
13. 如图，一个游戏转盘中，红、黄、蓝三个扇形的圆心角度数分别为60°、90°、210°．让转盘自由转动，则指针停止后落在红色区域的概率是 ．
14. 小明正在玩飞镖游戏，如果小明将飞镖随意投中如图所示的正方形木板，那么投中阴影部分的概率为.
15. 如图，在3×3的方格中，A、B、C、D、E、F分别位于格点上，从C、D、E、F四点中任取一点，与点A、B为顶点作三角形，则所作三角形为等腰三角形的概率是 ．
16. 如图，在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点，任意三个格点组成的三角形面积如果不小于1则称为“离心三角形”，而如果面积恰好等于1则称为“环绕三角形”。A，B是网格图形中已知的两个格点， 点C是另一格点， 且满足△ABC是“离心三角形”，则△ABC是“环绕三角形”的概率是 。
17. 一只蚂蚁在如图所示的七巧板上任意爬行，已知它停在这副七巧板上的任何一点的可能性都相同，那它停在4号板上的概率是.
18. 正多面体只有五种，分别是正四面体，正六面体，正八面体，正十二面体和正二十面体．如图是一枚质地均匀的正二十面体的骰子，其中的1个面标有“1”，2个面标有“2”，3个面标有“3”，4个面标有“4”，5个面标有“5”，其余的面标有“6”．将这枚骰子随机掷出后，“6”朝上的概率是 ．
三、解答题
-
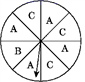
19. 某商人制成了一个如图所示的转盘，取名为“开心大转盘”，游戏规定：参与者自由转动转盘，转盘停止后，若指针指向字母“A”，则收费2元，若指针指向字母“B”，则奖励3元；若指针指向字母“C”，则奖励1元.一天，前来寻开心的人转动转盘80次，你认为该商人是盈利的可能性大还是亏损的可能性大？为什么？
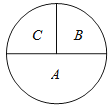
20.飞镖随机地掷在下面的靶子上（图中圆的半径平分半圆）
（1）飞镖投在区域A，B，C的概率各是多少？
（2）飞镖投在区域A或B中的概率是多少？
21.“六一”儿童节期间，某商厦为了吸引顾客，设立了一个可以自由转动的转盘（转盘被平均分成16份），并规定：顾客每购买100元的商品，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准哪个区域，顾客就可以获得相应的奖品．
颜色
奖品
红色
玩具熊
黄色
童话书
绿色
彩笔
小明和妈妈购买了125元的商品，请你分析计算：
（1）小明获得奖品的概率是多少？
（2）小明获得童话书的概率是多少？
22. “十一”黄金周期间，某商厦为了吸引顾客，设立了甲、乙两个可以自由转动的转盘，每个转盘被等分成3份，分别涂有不同颜色，商场规定顾客每购买100元的商品，就能获得一次参加抽奖的机会，规则是：分别转动甲、乙两个转盘各一次，转盘停止后，如果两个指针所指区域的颜色相同，顾客就可以获得一份奖品，若指针转到分割线上，则重新转动一次，小红的妈妈购买了125元的商品，请计算她妈妈获得奖品的概率．
四、综合题
-
23. 小丽和小刚都想参加学校组织的暑期实践活动，但只有一个名额，小丽提议：将一个转盘9等分，分別将9个区间标上1至9个9号码，随意转动－次转盘，根据指针指向区间决定谁去参加活动，具体规则：若指针指向偶数区间，小刚去参加活动；若指针指向奇数区间，小丽去参加活动．
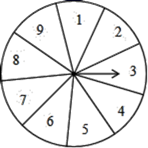(1)、求小刚去参加活动的概率是多少?(2)、你认为这个游戏公平吗?请说明理由．24. 小红和小明在操场做游戏，规则是：每人蒙上眼睛在一定距离外向设计好的图形内掷小石子，若掷中阴影部分则小红胜，否则小明胜，未掷入图形内则重掷一次.
(1)、若第一次设计的图形（图1）是半径分别为20cm和30cm的同心圆.求游戏中小红获胜的概率你认为游戏对双方公平吗？请说明理由.(2)、若第二次设计的图形（图2）是两个矩形，其中大矩形的长为80cm、宽为60cm，且小矩形到矩形的边宽相等.要使游戏对双方公平，则边宽x应为多少cm？25. 某班抽查25名学生数学测验成绩（单位：分），频数分布直方图如图：
(1)、成绩x在什么范围的人数最多？是多少人？(2)、若用半径为2的扇形图来描述，成绩在60≤x＜70的人数对应的扇形面积是多少？
(3)、从相成绩在50≤x＜60和90≤x＜100的学生中任选2人．小李成绩是96分，用树状图或列表法列出所有可能结果，求小李被选中的概率．