初中数学苏科版八年级上册第三章勾股定理单元测试

试卷更新日期：2020-11-04 类型：单元试卷

进入出卷网下载

一、单选题

1. 在△ABC，∠A，∠B，∠C的对应边分别是a，b，c，若∠B=90°，则下列等式中成立的是（）

A、a²+b²=c² B、b²+c²=a² C、 a²+c²=b² D、c²- a²= b²

查看试题解析
2. 由线段 $a, b, c$ 组成的三角形不是直角三角形的是（）

A、 $a = 3, b = 4, c = 5$ B、 $a = 8, b = 9, c = 10$ C、 $a = 15, b = 8, c = 17$ D、 $a = 12, b = 13, c = 5$

查看试题解析
3. 直角三角形中，两条直角边长分别是12和5，则斜边中线长是（）

A、26 B、13 C、 $\frac{60}{13}$ D、6.5

查看试题解析
4. 古代数学的“折竹抵地”问题：“今有竹高九尺，末折抵地，去本三尺，问折者高几何？”意思是：现有竹子高9尺，折后竹尖抵地与竹子底部的距离为3尺，问折处高几尺？即：如图，AB＋AC=9尺，BC=3尺，则AC等于（）尺．

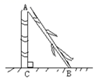A、3.5 B、4 C、4.5 D、5

查看试题解析
5. 以直角三角形的三边为边向外作正方形，其中两个正方形的面积如图所示，则正方形A的面积为（）

A、6 B、36 C、64 D、8

查看试题解析
6. 如图所示，有一个高 $16 c m$ ，底面周长为 $24 c m$ 的圆柱形玻璃容器，在外侧距下底 $2 c m$ 的点 $S$ 处有一只蚂蚁，与蚂蚁相对的圆柱形容器的上口内侧距开口处 $2 c m$ 的点 $F$ 处有一滴凝固的蜂蜜，则蚂蚁到凝固蜂蜜所走的最短路径的长度是（） $c m .$

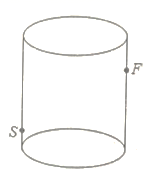A、 $12 \sqrt{2}$ B、20 C、24 D、28

查看试题解析
7. 如图是放在地面上的一个长方体盒子，其中AB=9cm，BC=6cm，BF=5cm，点M在棱AB上，且AM=3cm，点N是FG的中点，一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N，它需要爬行的最短路程为（）

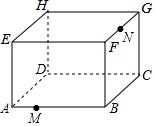A、10cm B、 $\sqrt{106} c m$ C、 $（ 6 + \sqrt{34} ） c m$ D、9cm

查看试题解析
8. 下列选项中，不能用来证明勾股定理的是（）

A、 B、 C、 D、

查看试题解析
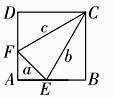9. 如图所示，是一张直角三角形的纸片，两直角边AC＝6㎝，BC＝8㎝，现将△ABC折叠，使点B与点A重合，折痕为DE，则AD的长为（）

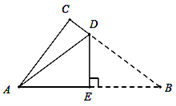A、4㎝ B、5㎝ C、6㎝ D、 $\frac{25}{4}$ ㎝

查看试题解析
10. 如图，四个全等的直角三角形围成一个正方形ABCD和正方形EFGH，即赵爽弦图，连接AC，FN交EF，GH分别于点M，N已知AH=3DH，且S_正方形_ABCD $= 21$ ，则图中阴影部分的面积之和为（）

A、 $\frac{21}{4}$ B、 $\frac{21}{5}$ C、 $\frac{22}{5}$ D、 $\frac{22}{3}$

查看试题解析

二、填空题

11. 如图，为修铁路需凿通隧道BC ，测得∠C＝90°，AB＝5km ， AC＝4km ，若每天凿隧道0.3km ，则需天才能把隧道凿通．

查看试题解析
12. 有一个三角形的两边长是9和12，要使这个三角形成为直角三角形，则第三条边长的平方是.

查看试题解析
13. 如图，在 $Rt Δ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 2 B C$ ，分别以点A和B为圆心，以大于 $\frac{1}{2} A B$ 的长为半径作弧，两弧相交于点M和N，作直线 $M N$ ，交 $A C$ 于点E，连接 $B E$ ，若 $C E = 3$ ，则 $B E$ 的长为.

查看试题解析
14. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ，若 $A B - A C = 2 ， B C = 8$ ，则 $A B$ 的长是．

查看试题解析
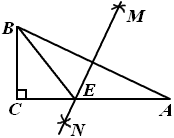15. 对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD，对角线AC、BD交于点O.若AD＝2，BC＝4，则AB²+CD²＝.

查看试题解析
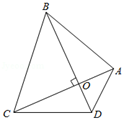16. 如图1，直角三角形纸片的一条直角边长为2，剪四块这样的直角三角形纸片，把它们按图2放入一个边长为3的正方形中(片在结合部分不重叠无缝隙)，则图2中阴影部分面积为。

查看试题解析
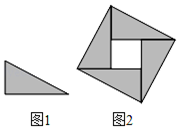17. 如图，所有阴影四边形都是正方形，两个空白三角形均为直角三角形，且A、B、C三个正方形的边长分别为2、3、4，则正方形D的面积为.

查看试题解析
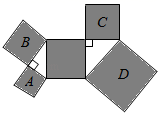18. 如图， $∠ A O B = 90 °$ ， $O A = 9 m$ ， $O B = 3 m$ ，一机器人在点B处看见一个小球从点A出发沿着 $A O$ 方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球，如果小球滚动的速度与机器人行走的速度相等，则机器人行走的路程BC为.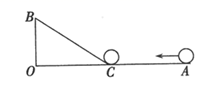

查看试题解析

三、解答题

19.
已知，在△ABC中，∠ACB=90°，CD⊥AB垂足为D，BC=6，AC=8，求AB与CD的长．

查看试题解析
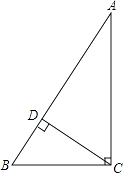20. 如图，一高层住宅发生火灾，消防车立即赶到距大厦9米处（车尾到大厦墙面），升起云梯到火灾窗口，已知云梯长15米，云梯底部距地面2米，问：发生火灾的住户窗口距离地面多高？

查看试题解析
21. 如图，AB⊥BC，CD⊥BC，点E在BC上，且AE＝DE. 若AB＝20，CD＝30，BC＝50，求AE的长.

查看试题解析
22. 如图，在Rt△ABC中，∠BCA＝90°，AC＝12，AB＝13，点D是Rt△ABC外一点，连接DC，DB，且CD＝4，BD＝3.求：四边形ABDC的面积.

查看试题解析
23. 如图，在△ABC和△DCE中，AC=DE，∠B=∠DCE=90，点A，C，D依次在同一直线上，且AB平行DE.

(1)、求证：△ABC≌△DCE

(2)、连结AE，当BC=5，AC=12时，求AE的长.

查看试题解析
24. 如图，已知正方体纸盒的表面积为12cm²；

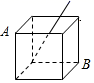(1)、求正方体的棱长；

(2)、剪去盖子后，插入一根长为5cm的细木棒，则细木棒露在外面的最短长度是多少？

(3)、一只蚂蚁在纸盒的表面由A爬到B，求蚂蚁行走的最短路线.

查看试题解析
25. 教材在探索平方差公式时利用了面积法，面积法除了可以帮助我们记忆公式，还可以直观地推导或验证公式，俗称“无字证明”，例如，著名的赵爽弦图（如图①，其中四个直角三角形较大的直角边长都为 $a$ ，较小的直角边长都为 $b$ ，斜边长都为 $c$ ），大正方形的面积可以表示为 $c^{2}$ ，也可以表示为 $4 \times \frac{1}{2} a b + {(a - b)}^{2}$ ，由此推导出重要的勾股定理：如果直角三角形两条直角边长为 $a ， b$ ，斜边长为 $c$ ，则 $a^{2} + b^{2} = c^{2}$ ．

(1)、图②为美国第二十任总统伽菲尔德的“总统证法”，请你利用图②推导勾股定理．

(2)、如图③，在 $△ A B C$ 中， $A D$ 是 $B C$ 边上的高， $A B = 4$ ， $A C = 5$ ， $B C = 6$ ，设 $B D = x$ ，求 $x$ 的值．

(3)、试构造一个图形，使它的面积能够解释 $(a + b) (a + 2 b) = a^{2} + 3 a b + 2 b^{2}$ ，画在如图4的网格中，并标出字母 $a ， b$ 所表示的线段．

查看试题解析

初中数学苏科版八年级上册第三章 勾股定理 单元测试

一、单选题

二、填空题

三、解答题

初中数学苏科版八年级上册第三章勾股定理单元测试