初中数学苏科版七年级上册第六章 平面图形的认识(一)单元测试
试卷更新日期:2020-11-03 类型:单元试卷
一、单选题
-
1. 如图,经过刨平的木板上的 两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
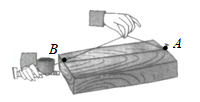 A、点动成线; B、两点确定一条直线; C、垂线段最短; D、两点之间,线段最短;2. 下列现象中,用“两点之间,线段最短”来解释的现象是( )A、用两个钉子把木条固定在墙上 B、利用圆规可以比较两条线段的大小 C、把弯曲的公路改直,就缩短路程 D、植树时,只要固定两棵树的位置,就能确定一行树所在的直线3. 下列4个图形中,能用 , , 三种方法表示同一个角的图形是( )A、
A、点动成线; B、两点确定一条直线; C、垂线段最短; D、两点之间,线段最短;2. 下列现象中,用“两点之间,线段最短”来解释的现象是( )A、用两个钉子把木条固定在墙上 B、利用圆规可以比较两条线段的大小 C、把弯曲的公路改直,就缩短路程 D、植树时,只要固定两棵树的位置,就能确定一行树所在的直线3. 下列4个图形中,能用 , , 三种方法表示同一个角的图形是( )A、 B、.
B、. 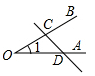 C、
C、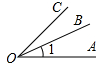 D、
D、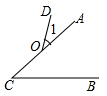 4. 下列换算中,错误的是( )A、47.28°=47°16'48'' B、83.5°=83°50' C、16°5'24''=16.09° D、0.25°=900''5. 如图,若 , 相交于点O,过点O作 ,则下列结论错误的是( )
4. 下列换算中,错误的是( )A、47.28°=47°16'48'' B、83.5°=83°50' C、16°5'24''=16.09° D、0.25°=900''5. 如图,若 , 相交于点O,过点O作 ,则下列结论错误的是( )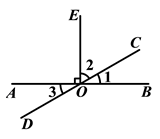 A、 与 互为余角 B、 与 互为余角 C、 与 互为补角 D、 与 是对顶角6. 如图,已知AB , CD相交于O , OE⊥CD于O , ∠AOC=25°,则∠BOE的度数是( )
A、 与 互为余角 B、 与 互为余角 C、 与 互为补角 D、 与 是对顶角6. 如图,已知AB , CD相交于O , OE⊥CD于O , ∠AOC=25°,则∠BOE的度数是( )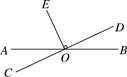 A、25° B、65° C、115° D、130°7. 如图,将一三角板按不同位置摆放,其中 与 互余的是(A、
A、25° B、65° C、115° D、130°7. 如图,将一三角板按不同位置摆放,其中 与 互余的是(A、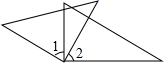 B、
B、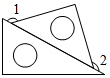 C、
C、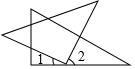 D、
D、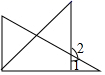 8. 下列说法中正确的个数有( )
8. 下列说法中正确的个数有( )①经过一点有且只有一条直线与已知直线垂直;②经过直线外一点,有且只有一条直线与已知直线平行;③连接直线外一点与直线上各点的所有线段中,垂线段最短;④两条直线相交,对顶角相等.
A、1个 B、2个 C、3个 D、4个9. 如图,点P到直线l的距离是( )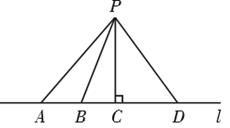 A、线段 的长度 B、线段 的长度 C、线段 的长度 D、线段 的长度10. 在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD, ∠AOC=30°时,∠BOD度数为( )A、60° B、120° C、60°或90° D、60°或120°
A、线段 的长度 B、线段 的长度 C、线段 的长度 D、线段 的长度10. 在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD, ∠AOC=30°时,∠BOD度数为( )A、60° B、120° C、60°或90° D、60°或120°二、填空题
-
11. 已知一个角的补角是它余角的3倍,则这个角的度数为.12. 如图, 垂足为O, 经过点O.则 的度数是 .
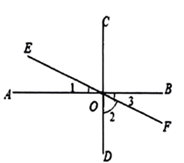 13. 如图,要从村庄P修一条连接公路 的最短的小道,应选择沿线段修建,理由是 .
13. 如图,要从村庄P修一条连接公路 的最短的小道,应选择沿线段修建,理由是 .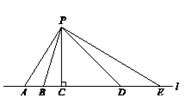 14. 如图是一把剪刀,若∠AOB+∠COD=60°,则∠BOD=°.
14. 如图是一把剪刀,若∠AOB+∠COD=60°,则∠BOD=°.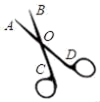 15. 如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段BN的长度,这样测量的依据是 .
15. 如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段BN的长度,这样测量的依据是 .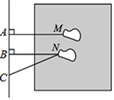 16. 26.54°=°′″.17.
16. 26.54°=°′″.17.如图,已知C、D是AB上两点,且AB=20cm,CD=6cm,M是AD的中点,N是BC的中点,则线段MN的长为cm.
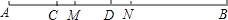 18. 已知A,B,C是数轴上的三个点,点A,B表示的数分别是1,3.如图所示,若BC=2AB,则点C表示的数是 .
18. 已知A,B,C是数轴上的三个点,点A,B表示的数分别是1,3.如图所示,若BC=2AB,则点C表示的数是 .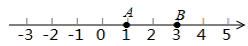
三、综合题
-
19. 计算:(1)、(2)、20. 如图,已知在平面上四点A,B,C,D,按下列要求画出图形;
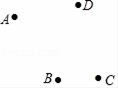 (1)、①射线AB,直线CB;
(1)、①射线AB,直线CB;②取线段AB的中点E,连接DE并延长与直线CB交于点O;
(2)、在所画的图形中,若AB=6,BE=BC= OB,求OC的长.21. 如图,在平面内有A,B,C三点。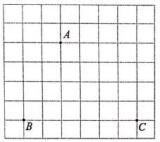 (1)、请按要求作图:画直线AC,射线BA,线段BC,取BC的中点D,过点D做DE⊥AC于点E。(2)、在完成第(1)小题的作图后,图中以A,B,C,D,E这些点为端点的线段共有条。22. 已知:如图,直线AB,CD相交于点O,OE⊥CD于点O,∠BOD=40°.求∠AOE的度数.
(1)、请按要求作图:画直线AC,射线BA,线段BC,取BC的中点D,过点D做DE⊥AC于点E。(2)、在完成第(1)小题的作图后,图中以A,B,C,D,E这些点为端点的线段共有条。22. 已知:如图,直线AB,CD相交于点O,OE⊥CD于点O,∠BOD=40°.求∠AOE的度数. 23. 已知如图,直线 相交于点 .
23. 已知如图,直线 相交于点 .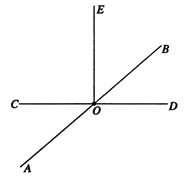 (1)、若∠AOC=35°,求 的度数;(2)、若∠BOD:∠BOC=2:4,求 的度数;(3)、在(2)的条件下,过点 作 ,求 的度数.24. 将一副三角板放在同一平面内,使直角顶点重合于点O
(1)、若∠AOC=35°,求 的度数;(2)、若∠BOD:∠BOC=2:4,求 的度数;(3)、在(2)的条件下,过点 作 ,求 的度数.24. 将一副三角板放在同一平面内,使直角顶点重合于点O
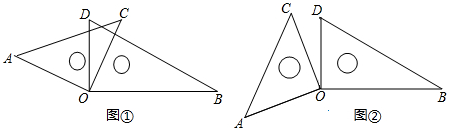 (1)、如图①,若∠AOB=155°,求∠AOD、∠BOC、∠DOC的度数.(2)、如图①,你发现∠AOD与∠BOC的大小有何关系?∠AOB与∠DOC有何关系?直接写出你发现的结论.(3)、如图②,当△AOC与△BOD没有重合部分时,(2)中你发现的结论是否还仍然成立,请说明理由.25. 如图,在数轴上有A,B两点,所表示的数分别为-10,-4,点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向右运动,设运动时间为t秒,解答下列问题:
(1)、如图①,若∠AOB=155°,求∠AOD、∠BOC、∠DOC的度数.(2)、如图①,你发现∠AOD与∠BOC的大小有何关系?∠AOB与∠DOC有何关系?直接写出你发现的结论.(3)、如图②,当△AOC与△BOD没有重合部分时,(2)中你发现的结论是否还仍然成立,请说明理由.25. 如图,在数轴上有A,B两点,所表示的数分别为-10,-4,点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向右运动,设运动时间为t秒,解答下列问题: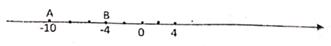 (1)、运动前线段AB的长为; 运动1秒后线段AB的长为;(2)、运动t秒后,点A,点B运动的距离分别为和。(3)、求t为何值时,点A和点B恰好重合;(4)、在上述运动过程中,是否存在某一时刻t使得线段AB的长为4,若存在,求出t的值:若不存在,请说明理由。
(1)、运动前线段AB的长为; 运动1秒后线段AB的长为;(2)、运动t秒后,点A,点B运动的距离分别为和。(3)、求t为何值时,点A和点B恰好重合;(4)、在上述运动过程中,是否存在某一时刻t使得线段AB的长为4,若存在,求出t的值:若不存在,请说明理由。