初中数学苏科版七年级上册第四章一元一次方程单元测试

试卷更新日期：2020-11-03 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列四个方程中，是一元一次方程的是（）

A、2x=3y B、7x+5=7（x－1） C、x²+3x－1=0 D、2x=4

查看试题解析
2. 若方程(m²－1)x²－mx－x＋2＝0是关于x的一元一次方程，则代数式|m－1|的值为（）

A、0 B、2 C、0或2 D、－2

查看试题解析
3. 如果关于x的方程3x+2k-5=0的解为x=-3，则k的值是（）

A、2 B、-2 C、7 D、-7

查看试题解析
4. 下列解方程中去分母正确的是（）

A、由 $\frac{x}{3} - 1 = \frac{1 - x}{2}$ ，得 $2 x - 1 = 3 - 3 x$ B、由 $\frac{x - 2}{2} - \frac{3 x - 2}{4} = - 1$ ，得 $2 (x - 2) - 3 x - 2 = - 4$ C、由 $\frac{y + 1}{2} = \frac{y}{3} - \frac{3 y - 1}{6} - y$ ，得 $3 y + 3 = 2 y - 3 y + 1 - 6 y$ D、由 $\frac{4 y}{5} - 1 = \frac{y + 4}{3}$ ，得 $12 y - 1 = 5 y + 20$

查看试题解析
5. 小马虎做作业时，不小心将方程中的一个常数污染了，被污染的方程是2（x－3）－■＝x＋1，怎么办呢？他想了想，便翻看书后的答案，方程的解是x＝9，请问这个被污染的常数是（　　）

A、1 B、2 C、3 D、4

查看试题解析
6. 在实数范围内定义运算“☆”： $a ☆ b = a + b - 1$ ，例如： $2 ☆ 3 = 2 + 3 - 1 = 4$ .如果 $2 ☆ x = 1$ ，则x的值是（）.

A、-1 B、1 C、0 D、2

查看试题解析
7. 某汽车队运送一批救灾物资，若每辆车装4吨，还剩8吨未装；若每辆车装4.5吨，恰好装完.设这个车队有 $x$ 辆车，则（）

A、 $4 (x + 8) = 4.5 x$ B、 $4 x + 8 = 4.5 x$ C、 $4.5 (x - 8) = 4 x$ D、 $4 x + 4.5 x = 8$

查看试题解析
8. 《九章算术》是我国古代数学名著，卷七“盈不足”中有题译文如下：今有人合伙买羊，每人出5钱，会差45钱；每人出7钱，会差3钱．问合伙人数、羊价各是多少？设合伙人数为 $x$ 人，所列方程正确是（　　）

A、 $5 x - 45 = 7 x - 3$ B、 $5 x + 45 = 7 x + 3$ C、 $\frac{x + 45}{5} = \frac{x + 3}{7}$ D、 $\frac{x - 45}{5} = \frac{x - 3}{7}$

查看试题解析
9. 天平呈平衡状态，其中左侧秤盘中有一袋玻璃球，右侧秤盘中也有一袋玻璃球，还有2个各20克的砝码．现将左侧袋中一颗玻璃球移至右侧秤盘，并拿走右侧秤盘的1个砝码后，天平仍呈平衡状态，如图2，则被移动的玻璃球的质量为（）

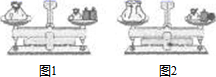A、10克 B、15克 C、20克 D、25克

查看试题解析
10. 把 $1 - 9$ 这 $9$ 个数填入 $3 \times 3$ 方格中，使其任意一行，任意一列及两条对角线上的数之和都相等，这样便构成了一个“九宫格”.它源于我国古代的“洛書”（图 $①$ ），是世界上最早的“幻方”.图 $②$ 是仅可以看到部分数值的“九宫格”，则其中 $x$ 的值为（）

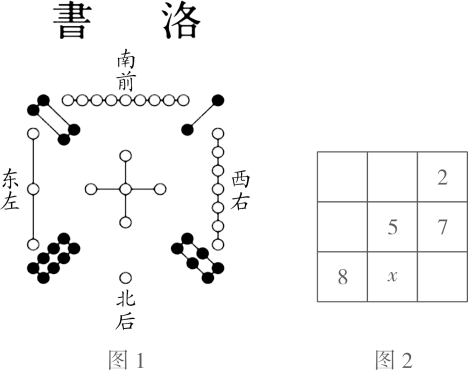A、1 B、3 C、4 D、6

查看试题解析

二、填空题

11. 当 $x = 3$ 时，式子 $2 x + 2$ 与 $5 x + k$ 的值相等，则 $k$ 的值是.

查看试题解析
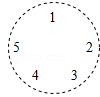
12. 足球比赛的计分规则为：胜一场积3分，平一场积1分，负1场积0分．初三．（1）班在校足球联赛中踢了17场，其中负4场，共积31分，那么这支足球队胜了场．

查看试题解析
13. 若方程 $\frac{x}{2} + \frac{m}{3} = x - 4$ 与方程 $\frac{1}{2} (x - 16) = - 6$ 的解相同，则m的值为．

查看试题解析
14. 若 $5 x^{m - 2} = 4$ 是一元一次方程，则m的值是．

查看试题解析
15. 规定：对于任意实数a，b都有：a⊕b=a（a-b）+1，其中等式右边是通常的加法、减法及乘法运算.如：2⊕5=2×（2-5）+1=2×（-3）+1=-5，那么等式3⊕x=16的解是.

查看试题解析
16. 5个人围成一个圆圈做游戏，游戏的规则是：每个人心里都想好一个实数，并把自己想好的数如实地告诉他相邻的两个人，然后每个人将他相邻的两个人告诉他的数的平均数报出来.若报出来的数如图所示，则报4的人心里想的数是．

查看试题解析
17. 李老师制作的PPT页面设置宽度与高度的比是4：3，宽度是25.6厘米，那么高度是厘米；如果宽度与高度的比是16：9，在宽度不变的情况下，高度应该是厘米。

查看试题解析
18. 将一张长为12.6m.宽为 $a c m (a > 6.3)$ 的长方形纸片按如图折叠出一个正方形，并将正方形剪下，这一过程称为第一次操作，将余下的长方形纸片再次折叠出一个正方形，并把正方形再剪下，则称为第二次操作，……，如此操作下去，若前四次剪下后的长方形纸片长与宽之比都小于2：1，当第五次操作后，剩下图形的长与宽之比为2：1，则 $a =$ $c m$ .

查看试题解析

三、解答题

19. 解下列方程。

(1)、2x-3=x+1

(2)、 $3 - \frac{x - 1}{2} = 3 x - 1$

查看试题解析
20. 假期期间，小明、小刚各随同家长共15人去某景点游玩，大人票每张100元，学生票8折优惠，买门票时共花费1380元．你能通过计算知道他们几个成人？几个学生吗？

查看试题解析
21. 中国古代数学著作《孙子算经》中有这样一个问题，原文：今有三人共车，二车空；二人共车，九人步，人与车各几何？译文为：今有若干人乘车，每3人共乘一车，所乘车都坐满，最终剩余2辆车，若每2人共乘一车，最终剩余9个人无车可乘，问共有多少人，多少辆车？

查看试题解析
22. 某市百货商场元旦期间搞促销活动，购物不超过200元不给优惠；超过200元，而不足500元，优惠10%，超过500元的，其中500元按9折优惠，超过部分按8折优惠，某人两次购物分别用了134元和466元，问：

(1)、此人两次购物其物品不打折值多少钱?

(2)、在这次活动中他节省了多少钱?

(3)、若此人将这两次的钱合起来购同一商品是更节省还是亏损?说明理由.

查看试题解析
23. 甲乙两个工程队承包了地铁某标段全长3900米的施工任务，分别从南，北两个方向同时向前掘进。已知甲工程队比乙工程队平均每天多掘进0.4米经过13天的施工两个工程队共掘进了156米.

(1)、求甲，乙两个工程队平均每天各掘进多少米？

(2)、为加快工程进度两工程队都改进了施工技术，在剩余的工程中，甲工程队平均每天能比原来多掘进0.4米，乙工程队平均每天能比原来多掘进0.6米，按此施工进度能够比原来少用多少天完成任务呢？

查看试题解析
24. 将连续的奇数1，3，5，7，9，…，2019，排成如图所示的数阵，十字框能上下左右移动，可框住5个数。

(1)、如图，若十字框中间的数为25，这5个数的和是多少?

(2)、设十字框中间的数为a，用式了表示另外4个数。

(3)、框住的5个数的和能否等于2020，请说明理由。

(4)、框住的5个数的和最大是多少?(给出结果，不说理由。)

查看试题解析

初中数学苏科版七年级上册第四章 一元一次方程 单元测试

一、单选题

二、填空题

三、解答题

初中数学苏科版七年级上册第四章一元一次方程单元测试