初中数学苏科版七年级上册6.3 余角 补角 对顶角 同步练习
试卷更新日期:2020-11-03 类型:同步测试
一、单选题
-
1. 若∠A=23°,则∠A余角的大小是( )A、57° B、67° C、77° D、157°2. 如图,直线a,b相交于点O,如果 ,那么 是( )
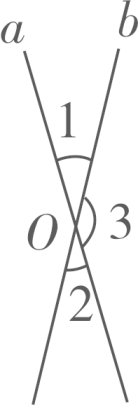 A、 B、 C、 D、3. 如果一个角的度数比它的补角的度数2倍多30°,那么这个角的度数是( )A、50° B、70° C、130° D、160°4. 已知锐角α,那么∠α的补角与∠α的余角的差是( )A、90° B、120° C、60°+α D、180°﹣α5. 下列关于余角、补角的说法,正确的是( )A、若∠1+∠2+∠3=90°,则∠1、∠2、∠3互余 B、若∠α+∠β+∠γ=180°,则∠α、∠β、∠γ互补 C、若∠1+∠2=90°,则∠1与∠2互补 D、若∠α+∠β=90°,则∠α与∠β互余6. 如图,直线a,b相交于点O,∠1=60°,则∠2=( )
A、 B、 C、 D、3. 如果一个角的度数比它的补角的度数2倍多30°,那么这个角的度数是( )A、50° B、70° C、130° D、160°4. 已知锐角α,那么∠α的补角与∠α的余角的差是( )A、90° B、120° C、60°+α D、180°﹣α5. 下列关于余角、补角的说法,正确的是( )A、若∠1+∠2+∠3=90°,则∠1、∠2、∠3互余 B、若∠α+∠β+∠γ=180°,则∠α、∠β、∠γ互补 C、若∠1+∠2=90°,则∠1与∠2互补 D、若∠α+∠β=90°,则∠α与∠β互余6. 如图,直线a,b相交于点O,∠1=60°,则∠2=( ) A、120° B、60° C、30° D、15°7. 如图,直线 与 相交于点 , 为 的角平分线,若 ,则 的度数为( )
A、120° B、60° C、30° D、15°7. 如图,直线 与 相交于点 , 为 的角平分线,若 ,则 的度数为( ) A、25° B、26° C、27° D、28°8. 下列图形中的两个角互为补角的是( )
A、25° B、26° C、27° D、28°8. 下列图形中的两个角互为补角的是( )

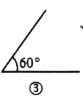
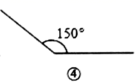 A、①和② B、①和③ C、①和④ D、③和④9. 将一副直角三角尺按如下不同方式摆放,则图中锐角∠1与∠2互余的是( ).A、
A、①和② B、①和③ C、①和④ D、③和④9. 将一副直角三角尺按如下不同方式摆放,则图中锐角∠1与∠2互余的是( ).A、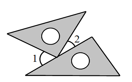 B、
B、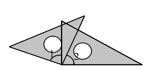 C、
C、 D、
D、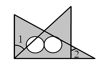 10. 已知∠1和∠2互为余角,∠1和∠3互为补角,∠2和∠3的和等于周角的 ,∠则∠1,∠2,∠3的度数分别为( )A、50°,40°,130° B、60°,30°,120° C、70°,20°,110° D、75°,15°,105°
10. 已知∠1和∠2互为余角,∠1和∠3互为补角,∠2和∠3的和等于周角的 ,∠则∠1,∠2,∠3的度数分别为( )A、50°,40°,130° B、60°,30°,120° C、70°,20°,110° D、75°,15°,105°二、填空题
-
11. 如图,点O在直线 上, ,则 的度数是 .
 12. 如果∠1与∠2互余,∠2与∠3互余,且∠1=25°,则∠3=.13. 如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM的度数是.
12. 如果∠1与∠2互余,∠2与∠3互余,且∠1=25°,则∠3=.13. 如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM的度数是.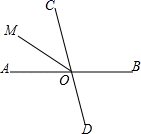 14. 如图,直线AB与CD相交于点O,且∠1+∠2=60°,则∠AOD的度数为.
14. 如图,直线AB与CD相交于点O,且∠1+∠2=60°,则∠AOD的度数为. 15. 如图,当剪子口 增大 时, 增大度,其根据是 .
15. 如图,当剪子口 增大 时, 增大度,其根据是 .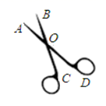 16. 如图,已知直线AB,CD,MN相交于O,若∠1=21°,∠2=47°,则∠3的度数为
16. 如图,已知直线AB,CD,MN相交于O,若∠1=21°,∠2=47°,则∠3的度数为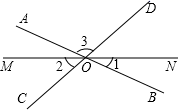 17. 若 与 互为补角, , ,且 ,则 的余角的度数是度.(结果用同时含m , n的代数式表示)18. 若一个角的补角比它的余角的 还多55°,则这个角为°.
17. 若 与 互为补角, , ,且 ,则 的余角的度数是度.(结果用同时含m , n的代数式表示)18. 若一个角的补角比它的余角的 还多55°,则这个角为°.三、解答题
-
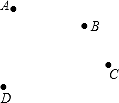
19. 如图,平面上有四个点A、B、C、D:
 (1)、根据下列语句画图:
(1)、根据下列语句画图:①射线BA;
②直线BD与线段AC相交于点E;
(2)、图中以E为顶点的角中,请写出∠AED的补角。20. 如图,直线AB , CD相交于O , OE是∠AOD的平分线,∠AOC=28°,求∠AOE的度数.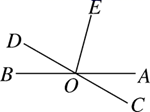 21. 如图,OC,OB,OD是 内三条射线,OB平分 ,OC平分 .
21. 如图,OC,OB,OD是 内三条射线,OB平分 ,OC平分 .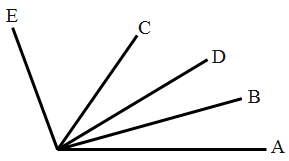 (1)、已知 , .求 的度数;(2)、设 ,用含a的代数式表示 ;(3)、若 与 互余,求 的度数.22. 如图,∠AOB是平角,OD是∠AOC的角平分线,∠COE=∠BOE.
(1)、已知 , .求 的度数;(2)、设 ,用含a的代数式表示 ;(3)、若 与 互余,求 的度数.22. 如图,∠AOB是平角,OD是∠AOC的角平分线,∠COE=∠BOE. (1)、若∠AOC= 50 ,则∠DOE= ;(2)、若∠AOC= 50 ,则图中与∠COD互补的角为;(3)、当∠AOC的大小发生改变时,∠DOE的大小是否发生改变?为什么?23. 如图,直线AB与CD相交于点E,射线EG在∠AEC内(如图1).
(1)、若∠AOC= 50 ,则∠DOE= ;(2)、若∠AOC= 50 ,则图中与∠COD互补的角为;(3)、当∠AOC的大小发生改变时,∠DOE的大小是否发生改变?为什么?23. 如图,直线AB与CD相交于点E,射线EG在∠AEC内(如图1).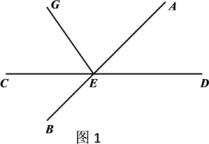
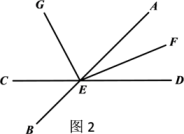 (1)、若∠BEC的补角是它的余角的3倍,则∠BEC=度;(2)、在(1)的条件下,若∠CEG比∠AEG小25度,求∠AEG的大小;(3)、若射线EF平分∠AED,∠FEG=100°(如图2),则∠AEG-∠CEG=度.24. 观察,在如图所示的各图中找对顶角(不含平角):
(1)、若∠BEC的补角是它的余角的3倍,则∠BEC=度;(2)、在(1)的条件下,若∠CEG比∠AEG小25度,求∠AEG的大小;(3)、若射线EF平分∠AED,∠FEG=100°(如图2),则∠AEG-∠CEG=度.24. 观察,在如图所示的各图中找对顶角(不含平角): (1)、如图a,图中共有对对顶角.(2)、如图b,图中共有对对顶角.(3)、如图c,图中共有对对顶角(4)、研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成多少对对顶角?(5)、若有2000条直线相交于一点,则可形成多少对对顶角?25. 如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC=50°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方。
(1)、如图a,图中共有对对顶角.(2)、如图b,图中共有对对顶角.(3)、如图c,图中共有对对顶角(4)、研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成多少对对顶角?(5)、若有2000条直线相交于一点,则可形成多少对对顶角?25. 如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC=50°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方。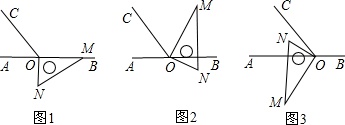 (1)、如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且OM恰好平分∠BOC.此时∠BON=度;(2)、如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;(3)、将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,若第t秒时,OA,OC,ON三条射线恰好构成相等的角,则t的值为(直接写出结果)
(1)、如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且OM恰好平分∠BOC.此时∠BON=度;(2)、如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;(3)、将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,若第t秒时,OA,OC,ON三条射线恰好构成相等的角,则t的值为(直接写出结果)