2016年高考文数真题试卷（北京卷）

试卷更新日期：2016-06-12 类型：高考真卷

进入出卷网下载

一、选择题（共8小题，每小题5分，满分40分）

1. 已知集合A={x|2＜x＜4}，B={x|x＜3或x＞5}，则A∩B=（　　）

A、{x|2＜x＜5} B、{x|x＜4或x＞5} C、{x|2＜x＜3} D、{x|x＜2或x＞5}

查看试题解析
2. 复数 $\frac{1 + 2 i}{2 - i} =$ （　　）

A、i B、1+i C、﹣i D、1﹣i

查看试题解析
3.
执行如图所示的程序框图，输出s的值为（　　）

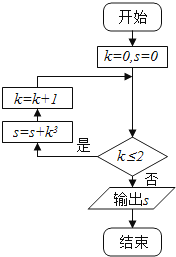A、8 B、9 C、27 D、36

查看试题解析
4. 下列函数中，在区间（﹣1，1）上为减函数的是（　　）

A、 $y = \frac{1}{1 - x}$ B、y=cosx C、y=ln（x+1） D、y=2^﹣^x

查看试题解析
5. 圆（x+1）²+y²=2的圆心到直线y=x+3的距离为（　　）

A、1 B、2 C、 $\sqrt{2}$ D、2 $\sqrt{2}$

查看试题解析
6. 从甲、乙等5名学生中随机选出2人，则甲被选中的概率为（　　）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{8}{25}$ D、 $\frac{9}{25}$

查看试题解析
7. 已知A（2，5），B（4，1）．若点P（x，y）在线段AB上，则2x﹣y的最大值为（　　）

A、﹣1 B、3 C、7 D、8

查看试题解析
8. 某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段，表中为10名学生的预赛成绩，其中有三个数据模糊．
学生序号
1
2
3
4
5
6
7
8
9
10
立定跳远（单位：米）
1.96
1.92
1.82
1.80
1.78
1.76
1.74
1.72
1.68
1.60
30秒跳绳（单位：次）
63
a
75
60
63
72
70
a﹣1
b
65
在这10名学生中，进入立定跳远决赛的有8人，同时进入立定跳远决赛和30秒跳绳决赛的有6人，则（　　）

A、2号学生进入30秒跳绳决赛 B、5号学生进入30秒跳绳决赛 C、8号学生进入30秒跳绳决赛 D、9号学生进入30秒跳绳决赛

查看试题解析

二、填空题（共6小题，每小题5分，满分30分）

9. 已知向量 $\vec{a}$ =（1， $\sqrt{3}$ ）， $\vec{b}$ =（ $\sqrt{3}$ ，1），则 $\vec{a}$ 与 $\vec{b}$ 夹角的大小为．

查看试题解析
10. 函数f（x）= $\frac{x}{x - 1}$ （x≥2）的最大值为．

查看试题解析
11.
某四棱柱的三视图如图所示，则该四棱柱的体积为．

查看试题解析
12. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）的一条渐近线为2x+y=0，一个焦点为（ $\sqrt{5}$ ，0），则a= ， b= ．

查看试题解析
13. 在△ABC中，∠A= $\frac{2 π}{3}$ ，a= $\sqrt{3}$ c，则 $\frac{b}{c}$ = ．

查看试题解析
14. 某网店统计了连续三天售出商品的种类情况：第一天售出19种商品，第二天售出13种商品，第三天售出18种商品；前两天都售出的商品有3种，后两天都售出的商品有4种，则该网店
①第一天售出但第二天未售出的商品有种；
②这三天售出的商品最少有种．

查看试题解析

三、解答题（共6小题，满分80分）

15. 已知{a_n}是等差数列，{b_n}是等比数列，且b₂=3，b₃=9，a₁=b₁ ， a₁₄=b₄ ．

(1)、求{a_n}的通项公式；

(2)、设c_n=a_n+b_n ，求数列{c_n}的前n项和．

查看试题解析
16. 已知函数f（x）=2sinωxcosωx+cos2ωx（ω＞0）的最小正周期为π．

(1)、求ω的值；

(2)、求f（x）的单调递增区间．

查看试题解析
17.
某市居民用水拟实行阶梯水价，每人月用水量中不超过w立方米的部分按4元/立方米收费，超出w立方米的部分按10元/立方米收费，从该市随机调查了10000位居民，获得了他们某月的用水量数据，整理得到如图频率分布直方图：

(1)、如果w为整数，那么根据此次调查，为使80%以上居民在该月的用水价格为4元/立方米，w至少定为多少？

(2)、假设同组中的每个数据用该组区间的右端点值代替，当w=3时，估计该市居民该月的人均水费．

查看试题解析
18.
如图，在四棱锥P﹣ABCD中，PC⊥平面ABCD，AB∥DC，DC⊥AC．

(1)、求证：DC⊥平面PAC；

(2)、求证：平面PAB⊥平面PAC；

(3)、设点E为AB的中点，在棱PB上是否存在点F，使得PA∥平面CEF？说明理由．

查看试题解析
19. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1过点A（2，0），B（0，1）两点．

(1)、求椭圆C的方程及离心率；

(2)、设P为第三象限内一点且在椭圆C上，直线PA与y轴交于点M，直线PB与x轴交于点N，求证：四边形ABNM的面积为定值．

查看试题解析
20. 设函数f（x）=x³+ax²+bx+c．

(1)、求曲线y=f（x）在点（0，f（0））处的切线方程；

(2)、设a=b=4，若函数f（x）有三个不同零点，求c的取值范围；

(3)、求证：a²﹣3b＞0是f（x）有三个不同零点的必要而不充分条件．

查看试题解析

学生序号	1	2	3	4	5	6	7	8	9	10
立定跳远（单位：米）	1.96	1.92	1.82	1.80	1.78	1.76	1.74	1.72	1.68	1.60
30秒跳绳（单位：次）	63	a	75	60	63	72	70	a﹣1	b	65