初中数学浙教版七年级上册第六章 图形的初步知识 单元检测(提高篇)
试卷更新日期:2020-11-03 类型:单元试卷
一、单选题
-
1. 几个同学在公园里玩、发现一个源亮的“古董”、甲:它有10个面乙:它由24条棱丙:它有8个面是正方形、2个面是多边形丁:如果把它们的侧面展开、是一个长方形、这个长方形有八种颜色、挺好看,通过这四个同学的对话、从几何体的名称来看、这个“古董”的形状可能是( )A、八棱柱 B、十棱柱 C、二十四棱柱 D、棱锥
-
2. 用边长为1的正方形纸板,制成一副七巧板(如图①),将它拼成“小天鹅”图案(如图②),其中阴影部分的面积为 ( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3. 下列各数中,正确的角度互化是( )A、 B、 C、 D、
-
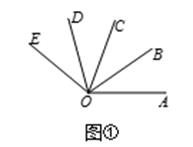
4. 如图,图中小于180°的角共有( )
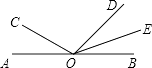 A、7个 B、9个 C、8个 D、10个
A、7个 B、9个 C、8个 D、10个 -
5. 在数轴上,点M、N分别表示数m,n. 则点M,N 之间的距离为|m-n|.已知点A,B,C,D在数轴上分别表示的数为a,b,c,d.且|a-c|=|b-c|= |d-a|=1 (a≠b),则线段BD的长度为( )A、3.5 B、0.5 C、3.5或0.5 D、4.5或0.5
-
6. 下列语句,正确的是( ).A、直线可表示一个平角; B、平角的两边向左右无限延伸; C、延长线段AB至点C,则∠ACB=180°; D、在一条直线上顺次取三点A、B、C,则∠ABC=180°
-
7. 在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD, ∠AOC=30°时,∠BOD度数为( )A、60° B、120° C、60°或90° D、60°或120°
-
8. 两个锐角的和( ).A、必定是锐角; B、必定是钝角; C、必定是直角; D、可能是锐角,可能是直角,也可能是钝角
-
9. 如图,已知A,O,B在一条直线上,∠1是锐角,则∠1的余角是( )
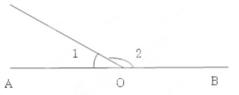 A、 B、 C、 D、∠2-∠1
A、 B、 C、 D、∠2-∠1 -
10. 如图所示,某公司有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
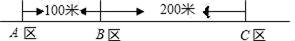 A、点A B、点B C、A,B之间 D、B,C之间
A、点A B、点B C、A,B之间 D、B,C之间
二、填空题
-
11. 如图,铁路上依次有A、B、C、D四个火车站,相邻两站之间的距离各不相同,则从A到B售票员应准备 种不同的车票.

-
12. 点A、B、C是同一直线上的三点,并且AB=10cm,BC=6cm.若点M是AB中点,点N是BC中点,则MN的长为 cm.
-
13. 一个角的余角的 3 倍比它的补角的 2 倍少 110°,则这个角的度数为.
-
14. 在同一平面内,两个角的两边分别垂直,其中一个角的度数是另一个角的 倍少 ,那么这两个度数分别是(只写数字,不写单位).
-
15. 已知在同一平面内,
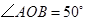 ,
,  ,则
,则 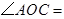 .
. -
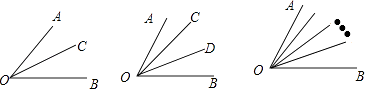
16. 以点O为端点引3条射线时,共有个角,引4条射线时,共有个角,以点O为端点引n条射线时,共有个角(用含n的字母表示).
三、解答题
-
17. 如图,已知四点 A,B,C,D,请按要求画图
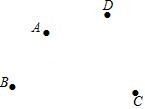
①画直线 AB,射线 CD 交于点 M
②连接 AC,BD 交于点 N
③连接 MN,并延长至点 E,使 NE=NM.
-
18.
(1)、一条直线可以把平面分成两个部分(或区域),如图,两条直线可以把平面分成几个部分?三条直线可以把平面分成几个部分?试画图说明.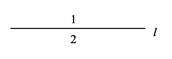 (2)、四条直线最多可以把平面分成几个部分?试画出示意图,并说明这四条直线的位置关系.
(2)、四条直线最多可以把平面分成几个部分?试画出示意图,并说明这四条直线的位置关系.
(3)、平面上有n条直线,每两条直线都恰好相交,且没有三条直线交于一点,处于这种位置的n条直线分一个平面所成的区域最多,记为 ,试研究 与n之间的关系. -
19.
 (1)、如图,点C在线段AB上,点M,N分别是线段AC,BC的中点.
(1)、如图,点C在线段AB上,点M,N分别是线段AC,BC的中点.
①若AC= 8 cm,CB= 6 cm,求线段MN的长;
②若AC+CB=a cm,直接写出线段MN的值.(2)、若C在线段AB的延长线上,且满足AC-BC = b cm,M,N分别为线段AC,BC的中点,直接写出线段MN=cm. -
20. 若 的度数是 的度数的k倍,则规定 是 的k倍角.
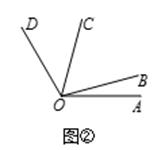 (1)、若∠M=21°17',则∠M的5倍角的度数为;(2)、如图1,OB是∠AOC的平分线,OD是∠COE的平分线,若∠AOC=∠COE,请直接写出图中∠AOB的所有3倍角;(3)、如图2,若∠AOC是∠AOB的5倍角,∠COD是∠AOB的3倍角,且∠AOC和∠BOD互为补角,求∠AOD的度数.
(1)、若∠M=21°17',则∠M的5倍角的度数为;(2)、如图1,OB是∠AOC的平分线,OD是∠COE的平分线,若∠AOC=∠COE,请直接写出图中∠AOB的所有3倍角;(3)、如图2,若∠AOC是∠AOB的5倍角,∠COD是∠AOB的3倍角,且∠AOC和∠BOD互为补角,求∠AOD的度数. -
21. 如图
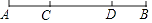 (1)、观察思考
(1)、观察思考如图,线段AB上有两个点C、D,请分别写出以点A、B、C、D为端点的线段,并计算图中共有多少条线段;
(2)、模型构建如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的正确性;
(3)、拓展应用8位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行多少场比赛?
请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.
-
22. 点A、B在数轴上表示的数如图所示,动点P从点A出发,沿数轴向右以每秒1个单位长度的速度向点B运动到点B停止运动;同时,动点Q从点B出发,沿数轴向左以每秒2个单位长度的速度向点A运动,到点A停止运动设点P运动的时间为t秒,P、Q两点的距离为d(d≥0)个单位长度.
 (1)、当t=1时,d=;(2)、当P、Q两点中有一个点恰好运动到线段AB的中点时,求d的值;(3)、当点P运动到线段AB的3等分点时,直接写出d的值;(4)、当d=5时,直接写出t的值.
(1)、当t=1时,d=;(2)、当P、Q两点中有一个点恰好运动到线段AB的中点时,求d的值;(3)、当点P运动到线段AB的3等分点时,直接写出d的值;(4)、当d=5时,直接写出t的值. -
23. 已知:直线AB,CD相交于点O,且OE⊥CD,如图.
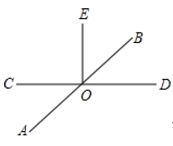 (1)、过点O作直线MN⊥AB;
(1)、过点O作直线MN⊥AB;
(2)、若点F是(1)中所画直线MN上任意一点(O点除外),且∠AOC=35°,求∠EOF的度数;
(3)、若∠BOD:∠DOA=1:5,求∠AOE的度数.
-
24. 定义:从一个角的顶点出发,把这个角分成1:2的两个角的射线,叫做这个角的三分线,显然,一个角的三分线有两条.例如:如图1所示,若∠BOC=2∠AOC,则OC是∠AOB的一条三分线.
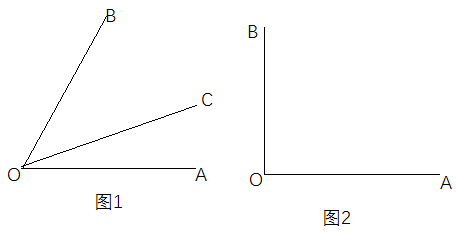 (1)、如图1所示,OC是∠AOB的一条三分线,且∠BOC>∠AOC,若∠AOB=60°,求∠AOC的度数:(2)、已知∠AOB=90°,如图2所示,若OC,OD是∠AOB的两条三分线.
(1)、如图1所示,OC是∠AOB的一条三分线,且∠BOC>∠AOC,若∠AOB=60°,求∠AOC的度数:(2)、已知∠AOB=90°,如图2所示,若OC,OD是∠AOB的两条三分线.①求∠COD的度数;
②现以点O为中心,将∠COD顺时针旋转n度得到∠C’DD’,当OA恰好是∠C’OD’的三分线时,求n的值.
